动作合成

20.2. 动作合成#

利用上一节的动捕技术，我们可以得到一系列动作数据，接下来我们会介绍利用这些数据能够完成哪些任务。

20.2.1. 动作数据#

在开始之前，我们首先需要了解动作数据在计算机中是以什么样的格式存储的。动捕数据一般以 BVH 文件（Biovision Hierarchy 文件）的形式存储，这类文件一般包含两部分（如图 20.13）：

  1. 动捕角色在 T 型姿势下的大小和姿态。

  2. 每一帧的角色姿态描述。这部分信息被表示成一个集合 \(\{\boldsymbol p_t\}\)，每一帧的信息 \(\boldsymbol p_t\) 形如 \(\boldsymbol p_t=(\boldsymbol t_0,\boldsymbol R_0,\boldsymbol R_1,\boldsymbol R_2,\cdots)\)，其中 \(\boldsymbol t_0\) 表示角色根节点（还记得 §19.2.1 中我们将人体骨骼结构抽象成一棵树吗？）的三维坐标，\(\boldsymbol R_0,\boldsymbol R_1,\boldsymbol R_2,\cdots\) 分别表示每个关节的旋转。

显然，我们可以根据文件中的数据还原出一个角色的动作序列。

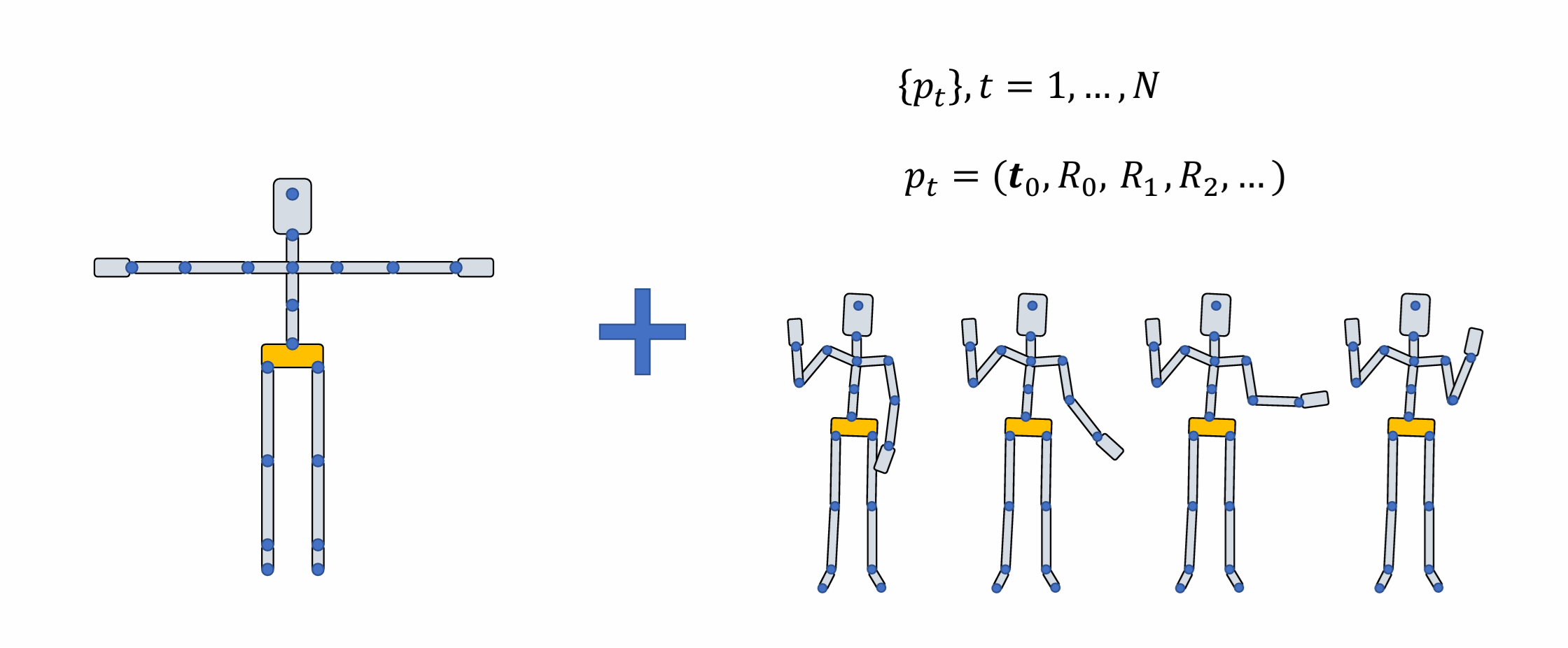
../../_images/animation-character-motion_data.png

图 20.13 动作数据#

利用这些数据通常分为几个环节（如图 20.14），首先需要把采集到的数据重定向（retargeting）到虚拟角色上，在此基础上我们需要对动作进行编辑（editing），然后进行动作的连接和混合（transition and blending），最后我们会把动作放到动作图（motion graph）中，实现可交互的动作组成（composition）和生成。

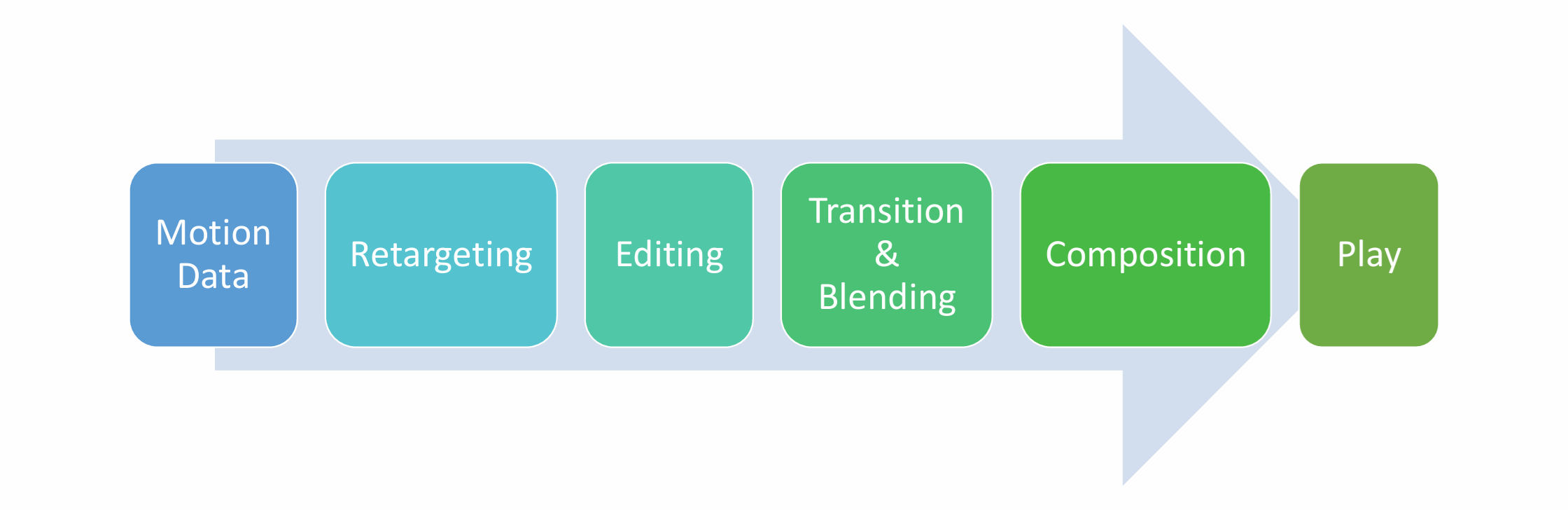
../../_images/animation-character-using_motion_data.png

图 20.14 动作数据的使用#

20.2.2. 动作重定向#

../../_images/animation-character-motion_retargeting.png

图 20.15 动作重定向#

一般来讲，动作捕捉的采集对象是人，而虚拟角色往往多种多样，其身体结构可能也会比人复杂得多，这个时候我们就需要进行动作重定向（如图 20.15）。和人相比，虚拟角色可能具有不同数量的骨骼、不同的骨骼名称、不同的静止姿态、不同的骨骼比例、不同的骨架结构等等。正是这种复杂性，使得重定向任务会遇到各种各样的问题，例如一些不够鲁棒的重定向会导致角色的脚底离开地面（如图 20.16(a)），或者出现穿模现象（如图 20.16(b)）。

(a) 角色脚底离开地面 (a) 角色脚底离开地面
(b) 穿模 (b) 穿模

图 20.16 动作重定向时会遇到的问题#

动作重定向的流程可以分为以下几步：

  1. 关节映射。 在动捕数据中的关节和虚拟角色的关节之间建立一个映射。

  2. 调整大小。 有时动捕数据中的长度单位与虚拟角色的不一致，动捕数据中的单位大多为米或英尺，而虚拟角色用的则可能是任何单位。这个步骤要处理的一个典型场景是走路的动作，对于这个场景我们通常会把根关节的位移缩放到高度与虚拟角色腿长相近，从而保证走路过程中脚不离地。

  3. 复制或重定向关节旋转以修正初始姿态。 为虚拟角色计算出每个关节的旋转以使它的初始姿态（T 型姿势或 A 型姿势，A 型姿势可参考 §20.3）能够匹配动捕数据的初始姿态。这个步骤在虚拟角色和动捕数据中的身体长度不一致时会比较繁琐，此时我们可以借助一些启发性的规则来确定关节旋转，例如对于动捕数据中没有出现的关节我们可以将其旋转设为零或设置为相邻关节旋转的平均值。

  4. 使用逆向运动学进行后处理，以解决诸如脚底打滑、穿模等问题。 这些问题往往需要调整关节位置来解决，仅仅修改动捕数据中的关节旋转是不够的，所以逆向运动学就不可避免。

为了更方便地进行重定向，业界提出了一些新的动捕数据的表示方式（其重定向效果如图 20.17），称为反向运动学绑定（IK rig）。在这种表示方式中，我们不再记录每个关节的旋转，而是记录一些关键关节的位置。于是我们只需要重定向相应关节的位置，再在虚拟角色上做逆向运动学，即可完成高质量的动作重定向。目前很热门的虚幻引擎（Unreal）也支持反向运动学绑定的格式（如图 20.18）。

../../_images/animation-character-ik_rig.png

图 20.17 反向运动学绑定原型#

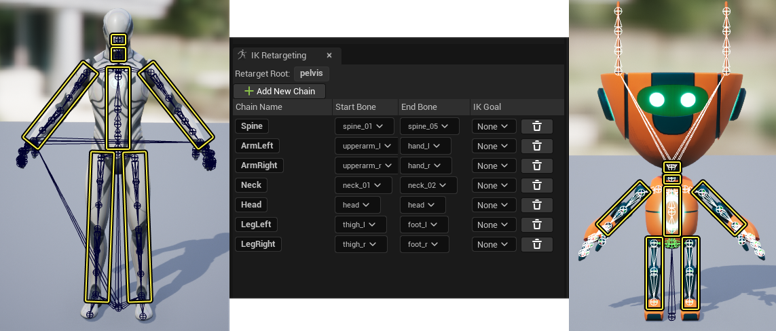
../../_images/animation-character-ik_rig_unreal.png

图 20.18 虚幻引擎中的反向运动学绑定#

20.2.3. 动作连接#

在完成动作重定向之后，我们还需要进行动作连接，这是因为我们采集到的动捕数据往往只是一个动作片段，为生成完整、流畅的动作还需要将多段动捕数据中的动作串联起来。例如我们现在已经重定向好了一段走路的动作和一段跑步的动作，我们想让虚拟角色先走路两秒钟，再跑步两秒钟，那么就需要借助动作连接技术从走路尽可能连贯地过渡到跑步。

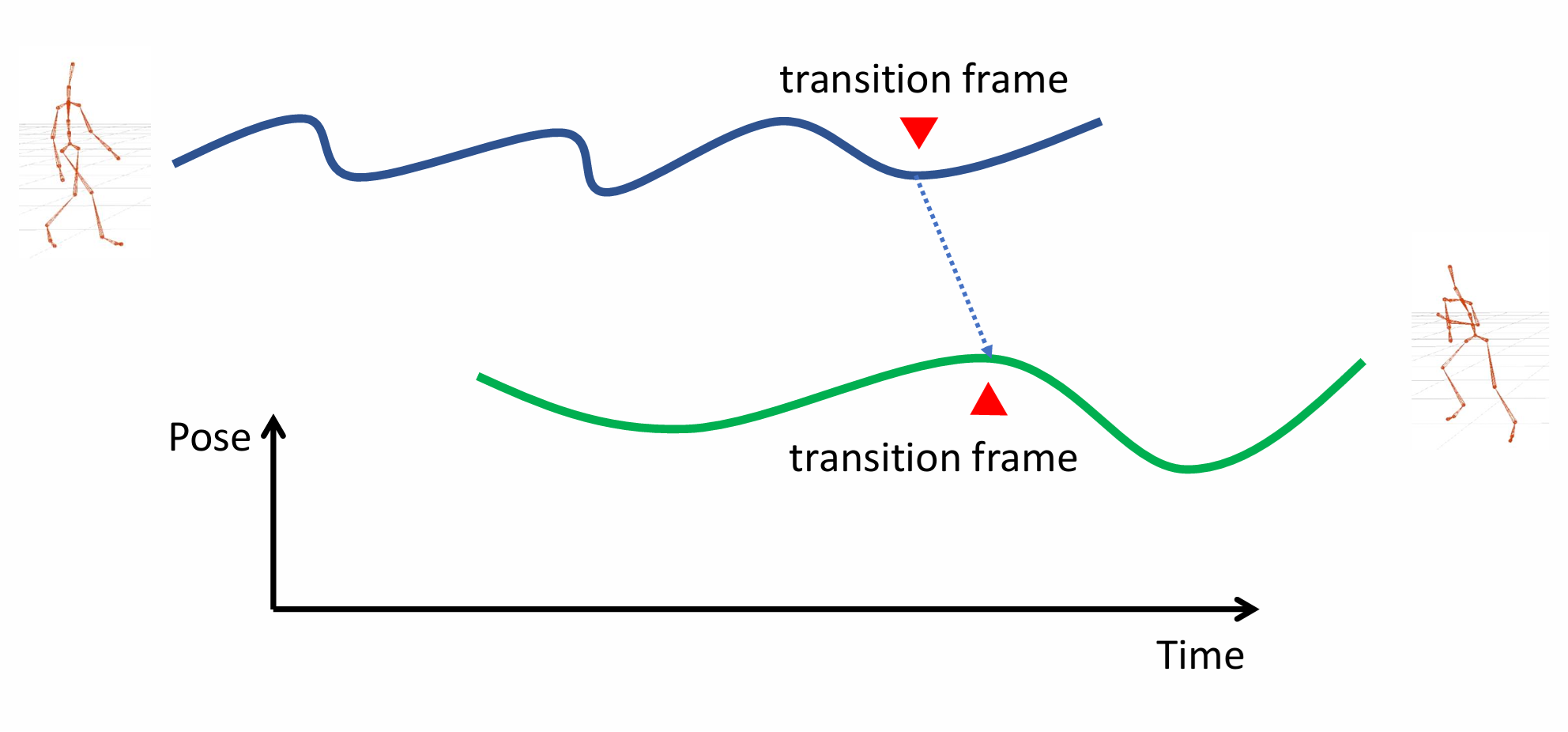
../../_images/animation-character-motion_transition1.png
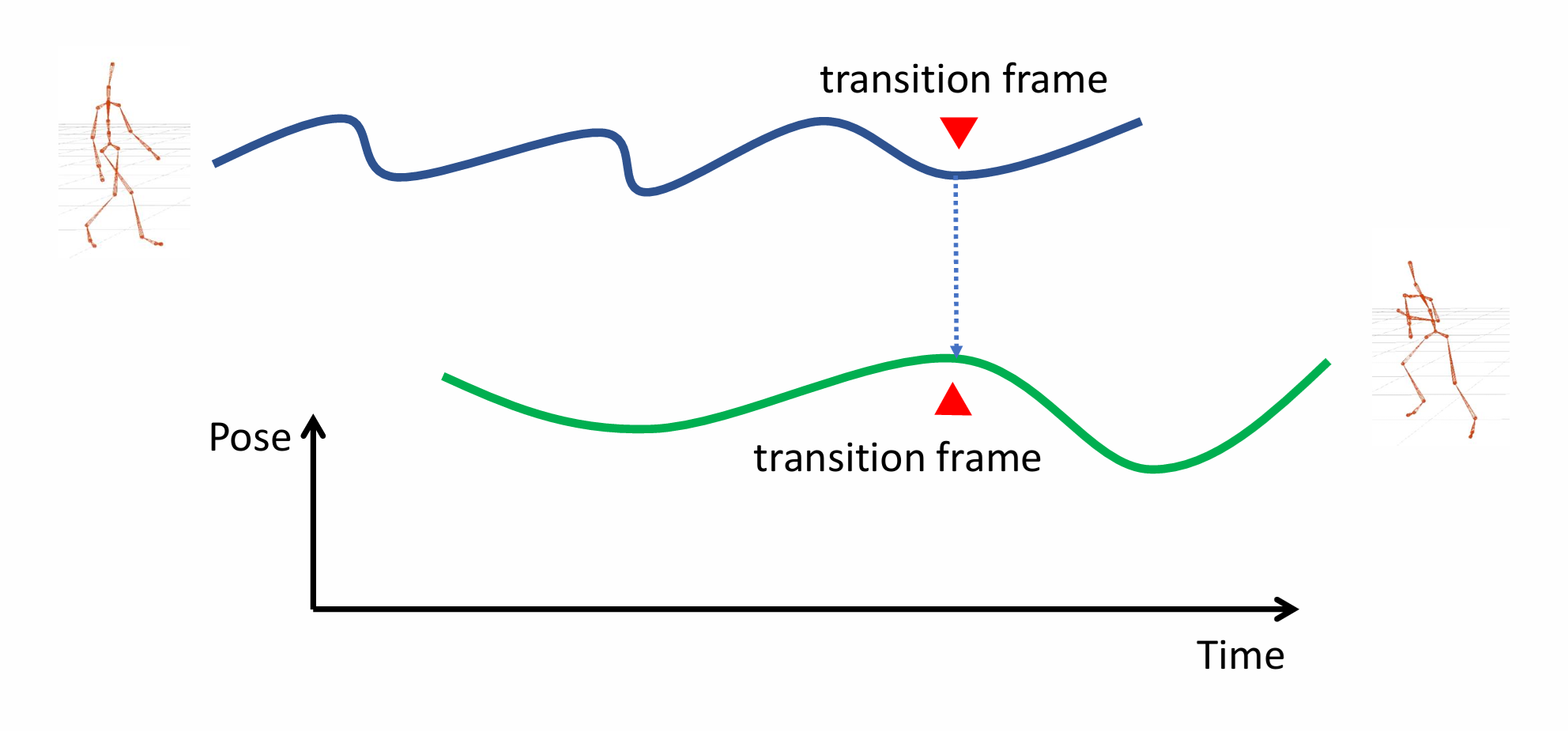
../../_images/animation-character-motion_transition2.png
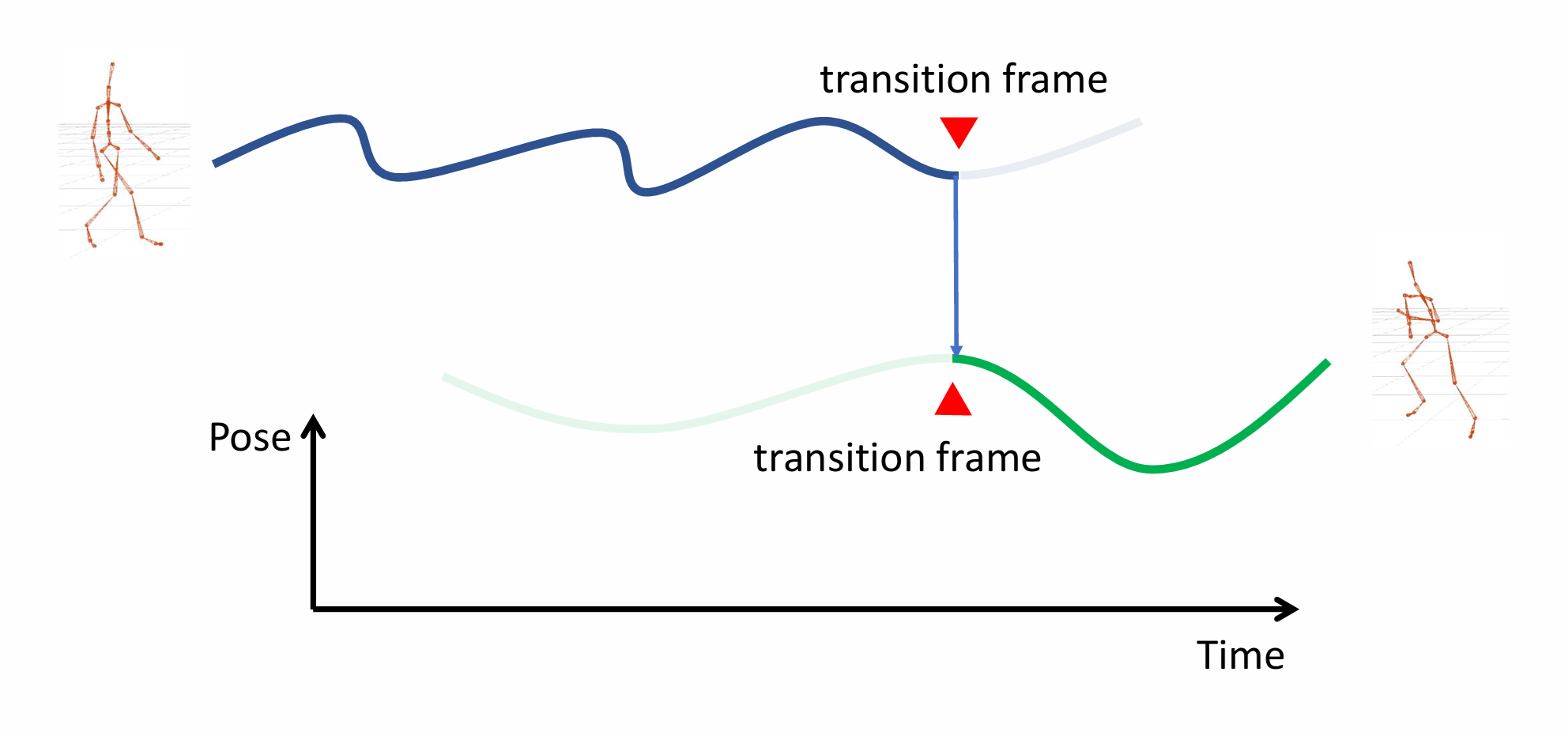
../../_images/animation-character-motion_transition3.png

图 20.19 动作连接的步骤#

20.2.3.1. 基础的动作连接方法#

我们假设需要连接的两个动作分别为动作 \(A\) 和动作 \(B\)，一个最简单的动作连接可以分为以下三步（如图 20.19）：

  1. 在 \(A\) 的动作序列和 \(B\) 的动作序列中分别挑选一帧，这两帧越相近越好，如图 20.19 中的过渡帧（transition frame）。

  2. 将 \(A\) 与 \(B\) 的动作序列进行时间对齐，使得挑选出的过渡帧处于同一时刻。

  3. 保留 \(A\) 序列过渡帧前的部分和 \(B\) 序列过渡帧后的部分，并直接拼接形成新的动作序列。

这个方法的缺点很明显：除非保证 \(A\)、\(B\) 动作在过渡帧完全相同，拼接处会出现一个不连续的跳变。但是这个方法在游戏中很常见，因为游戏中经常会有一些循环动作，角色在做完一个动作后总要恢复到动作开始前的姿态，比如我们经常看到一个角色做完“挥拳”或者“开枪”的动作之后总会恢复站立的姿态。

20.2.3.2. 平滑的动作连接#

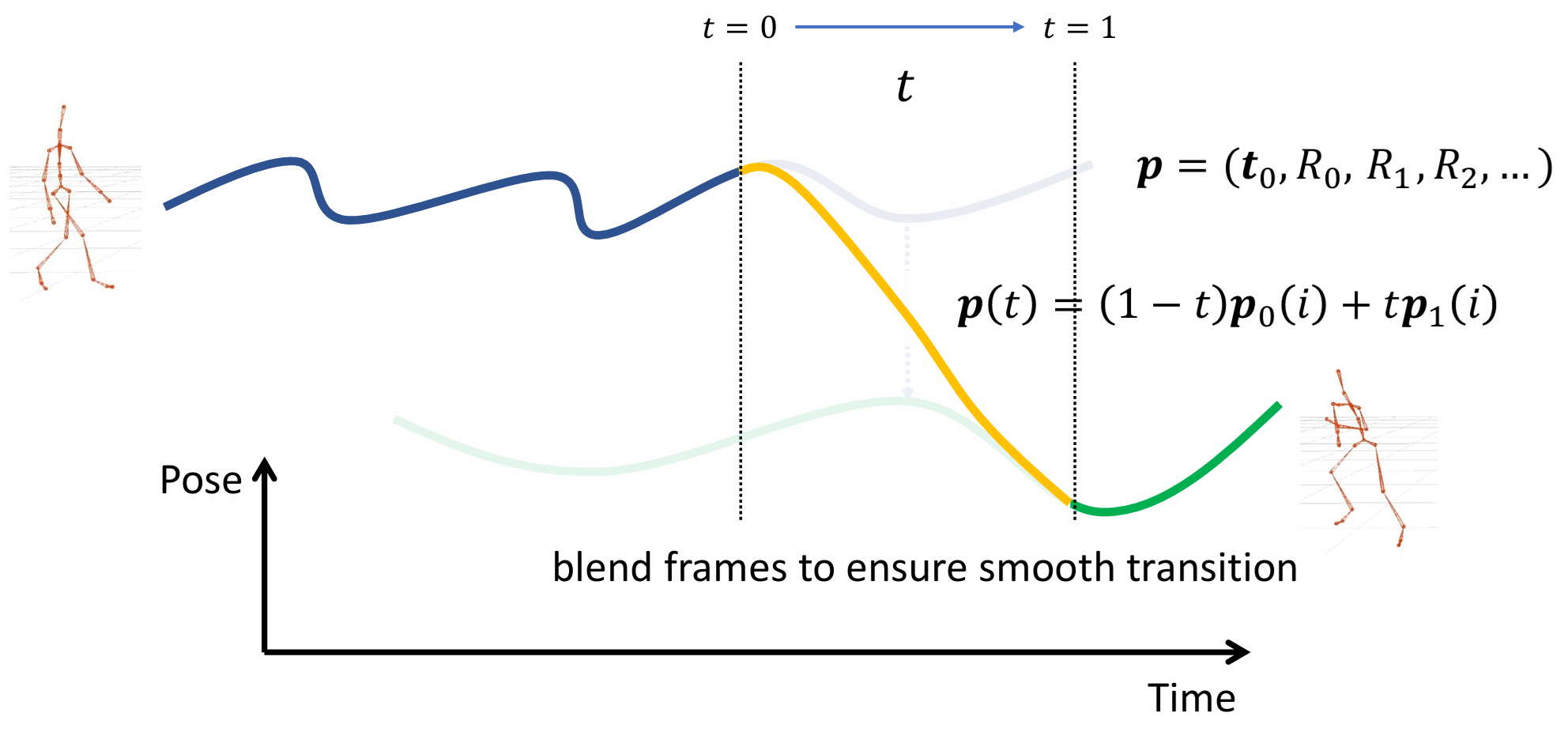
../../_images/animation-character-motion_transition_interpolation.png

图 20.20 平滑的动作连接#

在一般情况下，我们在动作过渡的时候需要做一个平滑操作。这时我们不应再只考虑一帧的切换，而是要考虑两个动作在过渡帧前后一段时间的序列。如图 20.20 所示，我们设这个过渡片段的开始时间为 \(0\)，结束时间为 \(1\)，再设动作序列 \(A\) 为 \(\boldsymbol p_0\)，\(B\) 为 \(\boldsymbol p_1\)，那么对于时刻 \(t\in[0,1]\)，我们的过渡动作可以取动作序列 \(A\) 和 \(B\) 的线性插值：

(20.1)#\[ \boldsymbol p(t)=(1-t)\boldsymbol p_0(i)+t\boldsymbol p_1(i) \]

其中 \(i\) 表示时刻 \(t\) 对应的帧数，使用这样的插值我们能做到在时间从 \(0\) 到 \(1\) 推进的过程中，角色动作会从 \(A\) 逐渐过渡到 \(B\)。为了达到一些特殊的平滑效果，我们也可以不使用线性插值，将式 (20.1) 中的 \(t\) 换成一个关于 \(t\) 的单调增函数 \(\phi(t)\in[0,1]\)，变成如下形式：

(20.2)#\[ \boldsymbol p(t)=(1-\phi(t))\boldsymbol p_0(i)+\phi(t)\boldsymbol p_1(i) \]

其中的 \(\phi(t)\) 可以取二次函数、指数函数等。

这里需要注意的一点是，在对 \(\boldsymbol p_0\) 和 \(\boldsymbol p_1\) 进行插值的时候，会涉及到对旋转的插值，此时不能像对位置插值一样简单的用线性组合计算插值后的结果，对旋转的插值读者可以回顾 §19.1.2.4 中介绍的方法。

20.2.3.3. 动作对齐#

至此我们已经能够较为平滑地拼接两段动作了，但是这样还会存在一个问题：例如动作 \(A\) 是一段向右的行走，动作 \(B\) 是一段向左的跑步，那么我们拼接之后会发现虚拟角色在从走切换到跑时突然调转了一个方向，并且在此过程中脚底还会出现明显的打滑现象。我们希望避免这种 \(180\) 度大转弯的现象，所以需要将 \(A\) 和 \(B\) 两段动作进行对齐（注意之前我们已经做过一次时间上的对齐了，现在我们要对齐的是 \(A\) 和 \(B\) 中人物的运动方向，如图 20.21）。

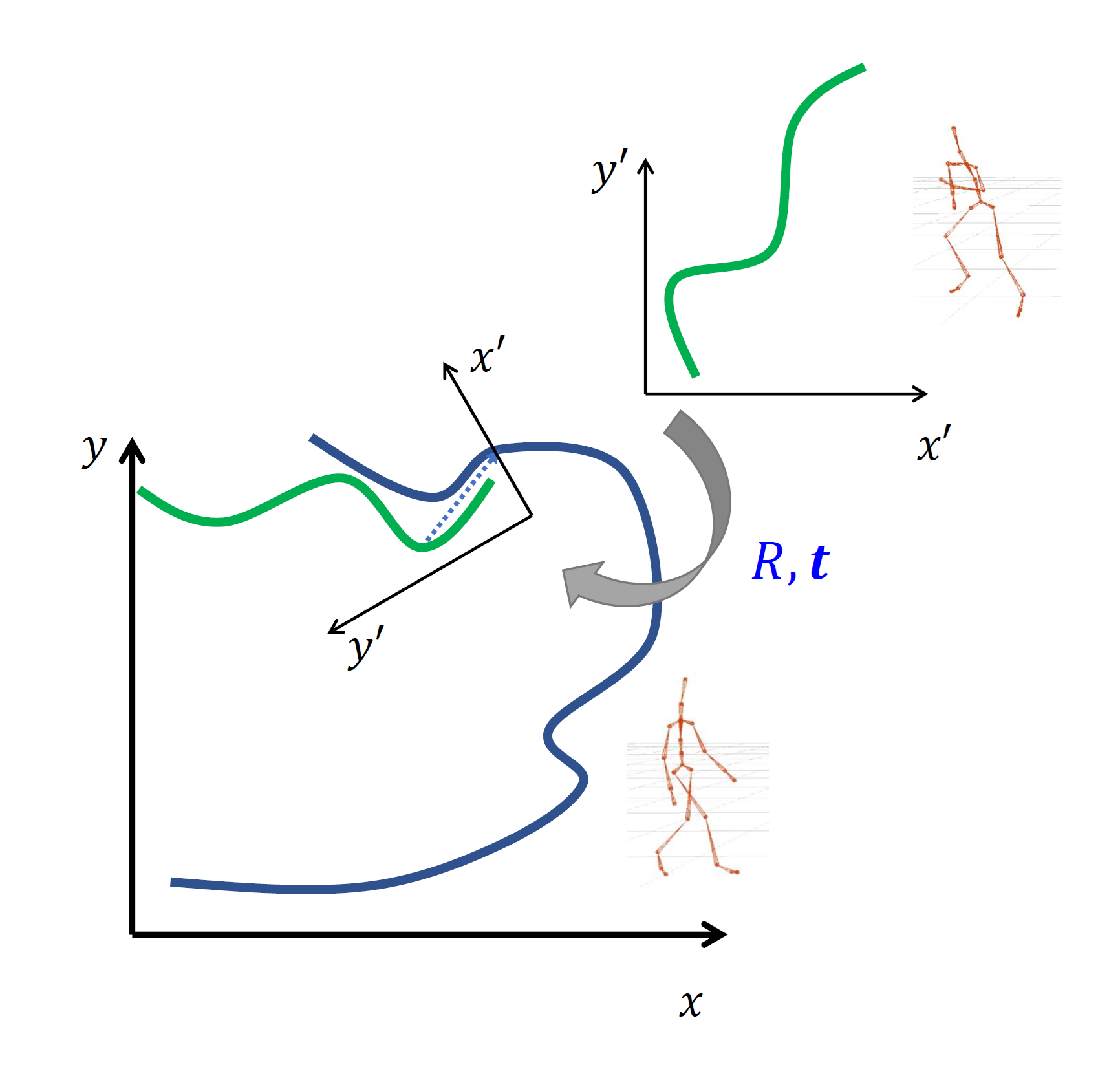
../../_images/animation-character-motion_transition_alignment.png

图 20.21 运动方向对齐#

在进行运动方向对齐之前，我们首先需要定义角色的朝向坐标系（facing frame），它是一个固定在角色身上的局部坐标系，一个局部坐标系可以由两个参数 \((\boldsymbol R,\boldsymbol t)\) 来表示，\(\boldsymbol R\) 表示局部坐标系在世界坐标系下的旋转（即世界坐标系的 \(3\) 个坐标轴在旋转 \(\boldsymbol R\) 变换下会变成局部坐标系的 \(3\) 个坐标轴在世界坐标系下的坐标），\(\boldsymbol t\) 表示局部坐标系的原点在世界坐标系下的位置。朝向坐标系的 \(\boldsymbol t\) 一般取根关节在世界坐标系下的坐标，\(\boldsymbol R\) 一般有如下两种选取方式：

  • \(\boldsymbol R\) 是一个绕 \(y\) 轴的旋转（见式 (19.4)），满足朝向坐标系的 \(z\) 轴指向角色的面朝方向。

  • \(\boldsymbol R\) 是一个绕 \(y\) 轴的旋转，满足朝向坐标系的 \(x\) 轴是世界坐标系中肩膀方向与臀部方向的平均方向。

我们采取前一种选取方式，图 20.22 展示了某时刻角色的朝向坐标系，这里我们采用了 \(y\) 轴向上的习惯定义坐标轴（图中没有显示与纸面垂直的 \(y\) 轴）。

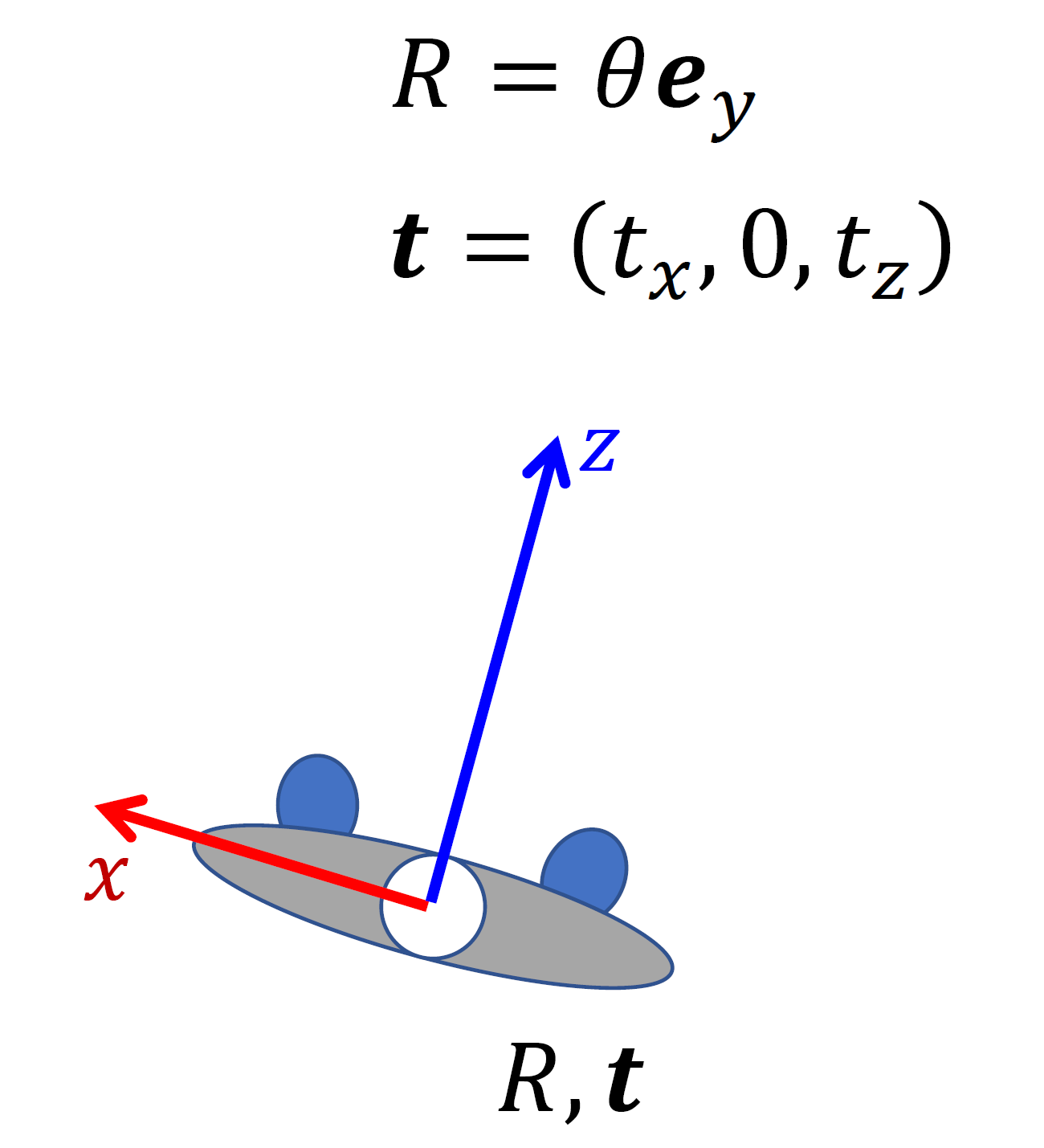
../../_images/animation-character-facing_frame.png

图 20.22 朝向坐标系。图为俯视角色视角，\(\boldsymbol R\) 采用轴角法表示，\(z\) 轴指向角色面朝方向，\(y\) 轴垂直纸面向外。#

接下来我们假设每一帧中的坐标都是在该帧的朝向坐标系下定义的。那么接下来我们可以将动作 \(B\) 在过渡帧时刻的朝向坐标系进行旋转、平移，使其变为与动作 \(A\) 在过渡帧时刻的朝向坐标系相同，并按照同样的旋转、平移去变换 \(B\) 序列中每一时刻的朝向坐标系（如图 20.23），记变换后的序列为 \(B'\)，那么我们对 \(A\) 和 \(B'\) 进行平滑操作即可。

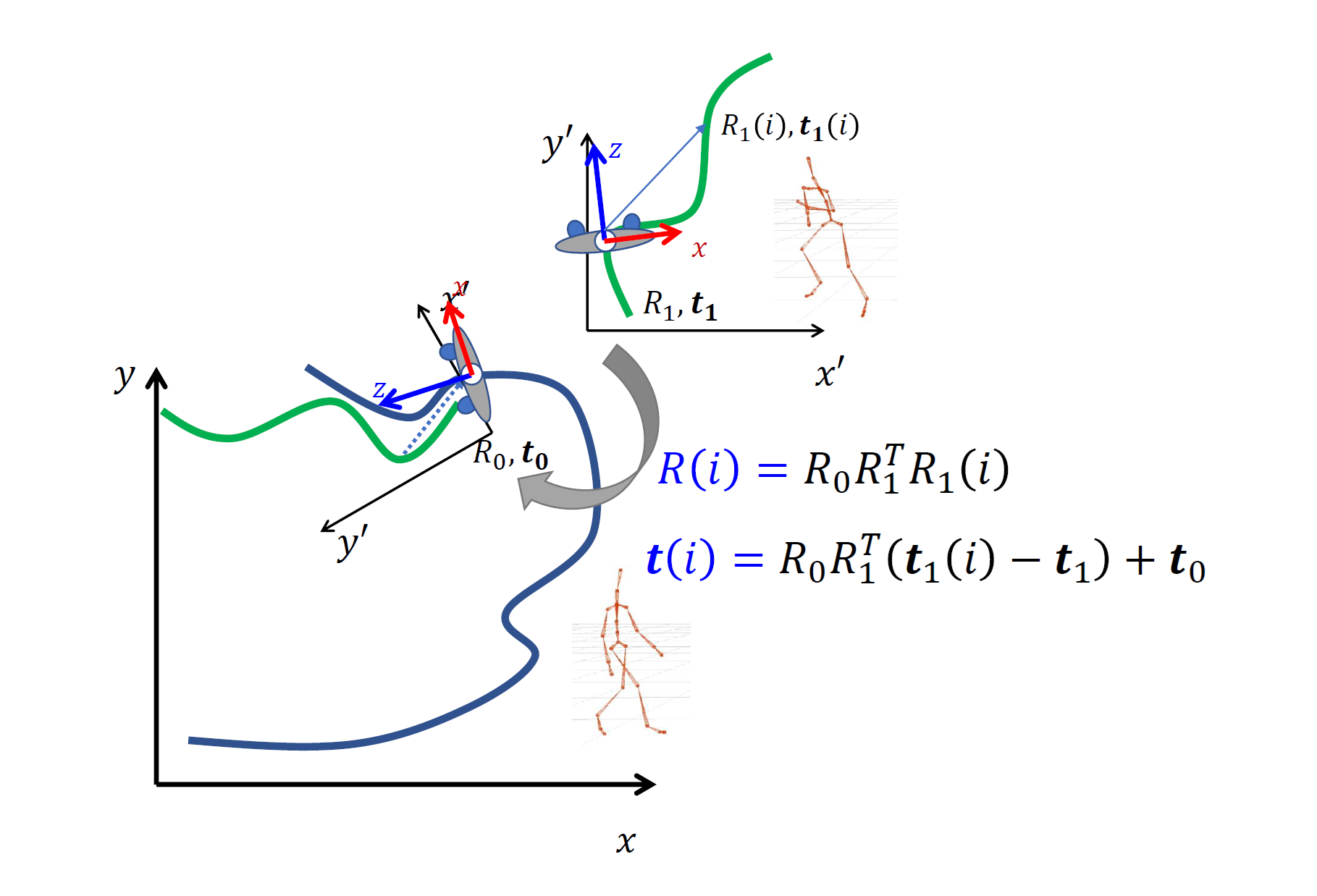
../../_images/animation-character-motion_transition_alignment_math.png

图 20.23 将两个序列进行运动方向对齐#

接下来的问题就在于如何计算这个“对齐变换”。参考图 20.23，我们考虑过渡帧后的某一帧 \(i\)，在 \(B\) 序列中的朝向坐标系为 \(\boldsymbol R_1(i),\boldsymbol t_1(i)\)，在 \(A\) 序列中的朝向坐标系为 \(\boldsymbol R(i),\boldsymbol t(i)\)，另外设过渡帧时刻 \(A\)、\(B\) 序列中的朝向坐标系分别为\(\boldsymbol R_0,\boldsymbol t_0\) 和 \(\boldsymbol R_1,\boldsymbol t_1\)，那么这其中只有 \(\boldsymbol R(i),\boldsymbol t(i)\) 是我们想求的变量，其余均为已知量。考虑在帧 \(i\) 时刻任取一个\(\boldsymbol R_1(i),\boldsymbol t_1(i)\) 坐标系下的三维坐标 \(\boldsymbol x\)，设其转换为 \(\boldsymbol R_1,\boldsymbol t_1\) 坐标系下的坐标为 \(\boldsymbol x_1\)；然后在 \(\boldsymbol R(i),\boldsymbol t(i)\) 坐标系下去同样的坐标 \(\boldsymbol x\)，设其转换为 \(\boldsymbol R_0,\boldsymbol t_0\) 坐标系下的坐标为 \(\boldsymbol x_0\)；那么我们应该有如下关系（这也是“对齐”的含义）：

(20.3)#\[ \boldsymbol x_0=\boldsymbol x_1。 \]

首先我们考虑如何将 \(\boldsymbol R_1(i),\boldsymbol t_1(i)\) 坐标系下的 \(\boldsymbol x\) 转换为 \(\boldsymbol x_1\)。这可以拆成两步来做：将 \(\boldsymbol x\) 转换为世界坐标系下的坐标 \(\boldsymbol x_B\)，然后将 \(\boldsymbol x_B\) 转换为 \(\boldsymbol x_1\)。第一步转换只需要将局部坐标系的旋转和平移依次作用在 \(\boldsymbol x\) 上：

(20.4)#\[ \boldsymbol x_B=\boldsymbol R_1(i)\boldsymbol x+\boldsymbol t_1(i)。 \]

第二步转换由于是世界坐标变为局部坐标，所以是一个逆变换，也就是先做平移的逆变换，再做旋转的逆变换：

(20.5)#\[ \boldsymbol x_1=\boldsymbol R_1^\top(\boldsymbol x_B-\boldsymbol t_1)。 \]

由式 (20.4) 和 (20.5) 可得

(20.6)#\[ \boldsymbol x_1=\boldsymbol R_1^\top[\boldsymbol R_1(i)\boldsymbol x+\boldsymbol t_1(i)-\boldsymbol t_1]。 \]

同理我们也可以得到 \(\boldsymbol x_0\) 与 \(\boldsymbol x\) 的关系：

(20.7)#\[ \boldsymbol x_0=\boldsymbol R_0^\top[\boldsymbol R(i)\boldsymbol x+\boldsymbol t(i)-\boldsymbol t_0]。 \]

那么由式 (20.3)、(20.6) 和 (20.7) 可得

\[ [\boldsymbol R_1^\top\boldsymbol R_1(i)-\boldsymbol R_0^\top\boldsymbol R(i)]\boldsymbol x=\boldsymbol R_0^\top\boldsymbol t(i)-\boldsymbol R_0^\top\boldsymbol t_0-\boldsymbol R_1^\top\boldsymbol t_1(i)+\boldsymbol R_1^\top\boldsymbol t_1。 \]

由 \(\boldsymbol x\) 的任意性可知

\[\begin{split} \begin{aligned} \boldsymbol R_1^\top\boldsymbol R_1(i)-\boldsymbol R_0^\top\boldsymbol R(i)&=\boldsymbol 0，\\ \boldsymbol R_0^\top\boldsymbol t(i)-\boldsymbol R_0^\top\boldsymbol t_0-\boldsymbol R_1^\top\boldsymbol t_1(i)+\boldsymbol R_1^\top\boldsymbol t_1&=\boldsymbol 0， \end{aligned} \end{split}\]

解得

\[\begin{split} \begin{aligned} \boldsymbol R(i)&=\boldsymbol R_0\boldsymbol R_1^\top\boldsymbol R_1(i)，\\ \boldsymbol t(i)&=\boldsymbol R_0\boldsymbol R_1^\top[\boldsymbol t_1(i)-\boldsymbol t_1]+\boldsymbol t_0。 \end{aligned} \end{split}\]

20.2.3.4. 曲线跟踪#

当然我们有时候并不需要进行对齐，比如你就想要实现一个走路过程中突然掉头跑步的效果，直接做插值就可以了。另外，很多时候我们拿到的动作数据已经去掉了全局的位置信息，即根关节的位置（有时也有朝向）不随时间变化，此时就不涉及到两段动作序列之间对齐的问题了，我们需要自己逐帧确定根关节的位置和朝向。这种去掉全局位置信息的动作数据在游戏中很常见，根关节的位置是游戏程序实时确定的，我们在网络卡顿的时候经常看到一个人在原地跑步就是由于在播放动作数据，但游戏程序的位置更新没有跟上。

使用没有全局位置信息的动作数据需要进行曲线跟踪（path fitting），我们需要手动指定角色根关节在一段时间内移动的路径（一般假定这个路径是在一个平面内），那么对于路径上任意一点，其切向即为角色的朝向，位置即为角色根关节的位置，由此可以确定出相应时刻下角色的朝向坐标系（如图 20.24）。

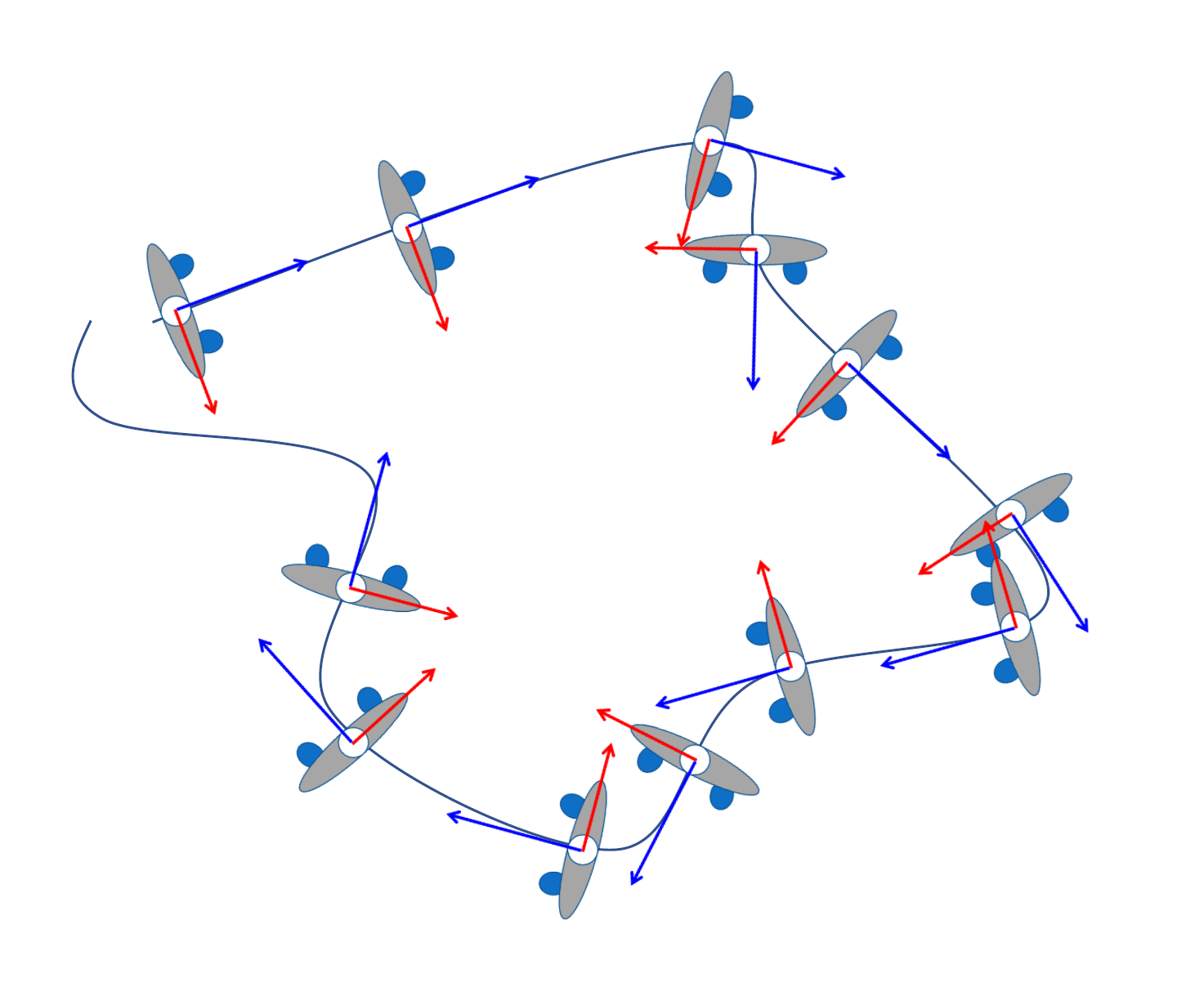
../../_images/animation-character-path_fitting.png

图 20.24 曲线跟踪#

20.2.4. 动作图#

至此，我们掌握的技术仅仅能够将两个动作平滑地链接在一起。但这还不够，我们还希望实现更加丰富的动作合成（motion composition），即希望让计算机能够自动化地计算出角色动画，使其能够支持：

  • 实时的用户控制。

  • 角色自动避开场景里的障碍物。

  • 与场景中其他角色进行交互。

  • 其他需要的功能或特性。

动作图 （motion graph）就是用来描述动作合成规则的数据结构。

动作图的本质是一个有限状态自动机（finite state automata），每个状态表示一个动作，状态之间如果满足一定条件就会发生转移，在动作图中。用一个节点表示一个状态，用一条有向边表示一个可能的转移，每一条边会对应一个转移条件，图 20.25 展示了一个简单的动作图。在生成一段动作时，我们会根据动作图，从某一个状态开始，当遇到用户输入打断或者当前动作播放完毕时，选择一个符合条件的转移并执行。在从一个动作状态转移到另一个动作状态时，我们可以使用前面介绍的插值方法做一个平滑的过渡。而对于如何选择下一个动作，取决于我们任务的复杂性，有时我们可以直接挑选一个合适的动作进行转移，有时则需要向后多考虑几步转移以进行更长远的规划（例如当我们让虚拟角色走上一个台阶时，需要指定每跨出一步后脚的位置，就可以借助深度优先搜索以做出后几步的规划）。

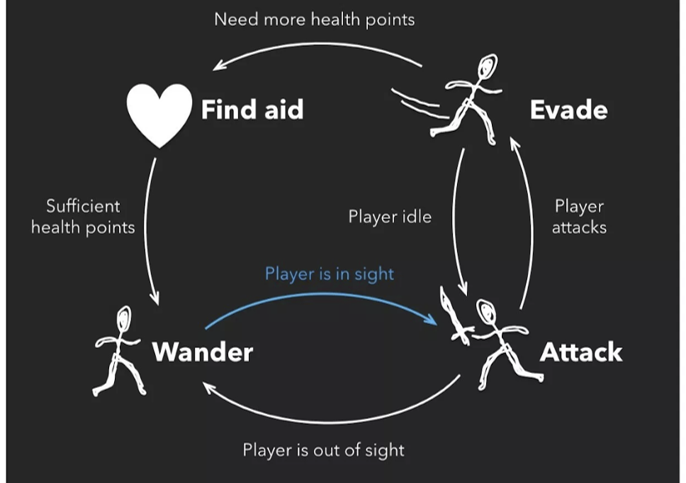
../../_images/animation-character-motion_graph.png

图 20.25 一个动作图#

../../_images/animation-character-motion_graph_matrix.png

图 20.26 由一段动捕数据构建出的一个矩阵。矩阵的元素值越大颜色越深，绿色的点为极小值点。#

那么给定一段动捕数据，如何生成一个动作图呢？假设动捕数据包含 \(n\) 帧，我们可以构造一个 \(n\times n\) 的矩阵（如图 20.26），第 \(i\) 行第 \(j\) 列元素表示第 \(i\) 帧动作与第 \(j\) 帧动作的距离。这里我们可以根据需要去定义一个距离，例如采用每个关节的旋转的距离，或是利用前向运动学计算每个关节的位置差，还可以考虑速度等信息。接下来我们找出矩阵元素中所有的极小值点，假设第 \(a\) 行第 \(b\) 列是一个极小值点，那么说明我们可以在动作的第 \(a\) 帧和第 \(b\) 帧进行一个分割，并且这两帧可以互相转移。这样根据所有的极小值点，我们可以将动捕数据分割成多个小段，每个小段可以作为动作图的一个节点，再通过潜在的转移关系在这些节点之间连边，从而构造出动作图。当然，直接这样构造出的动作图可能质量很差（比如它可能包含过多的状态，每个状态的动作太短），实践中还需要用户手动筛选一些极小值点，并做一些其他的处理。

总体而言，在动作图的基础上，我们实现动作合成是在以下步骤中不断循环的过程（每一帧执行一次这样的循环）：

  1. 检查用户输入。

  2. 检查当前场景的环境信息。

  3. 检查当前场景中是否存在需要互动的其他角色。

  4. 根据所有信息决定是否要进行状态转移。

  5. 在状态转移之后，要去获取下一个动作的姿态。

  6. 进行后处理。

  7. 更新角色姿态。

  8. 更新环境信息。

20.2.5. 其他动作合成方法#

动作图的应用虽然广泛，但是在实际应用的时候还需要很多的技巧和方法才能够生成高质量的动作合成。因此，人们提出了一些新的方法用于动作合成，包括动作匹配（motion matching）以及一些基于学习的方法。

动作匹配比动作图实现了更细粒度的动作控制，它会在每一帧都去判断下一帧要切换到哪个动作，切换的粒度不再是动作片段，而是姿态。这种细粒度的切换能够带来更快的用户操作响应，并且由于每一帧都会自动在动捕数据中搜索一帧最合适的姿态作为下一帧，它不再需要构建动作图时对数据的切割、建立转移等复杂的操作了。

随着机器学习的兴起以及生成模型的流行，这些方法也被引入到动作生成的任务当中来。相比传统的基于数据的方法，基于学习的方法不再是对数据的简单重组，而是会从数据中提取一些模型并用于生成。图 20.27 展示了两种基于学习的动作合成工作。

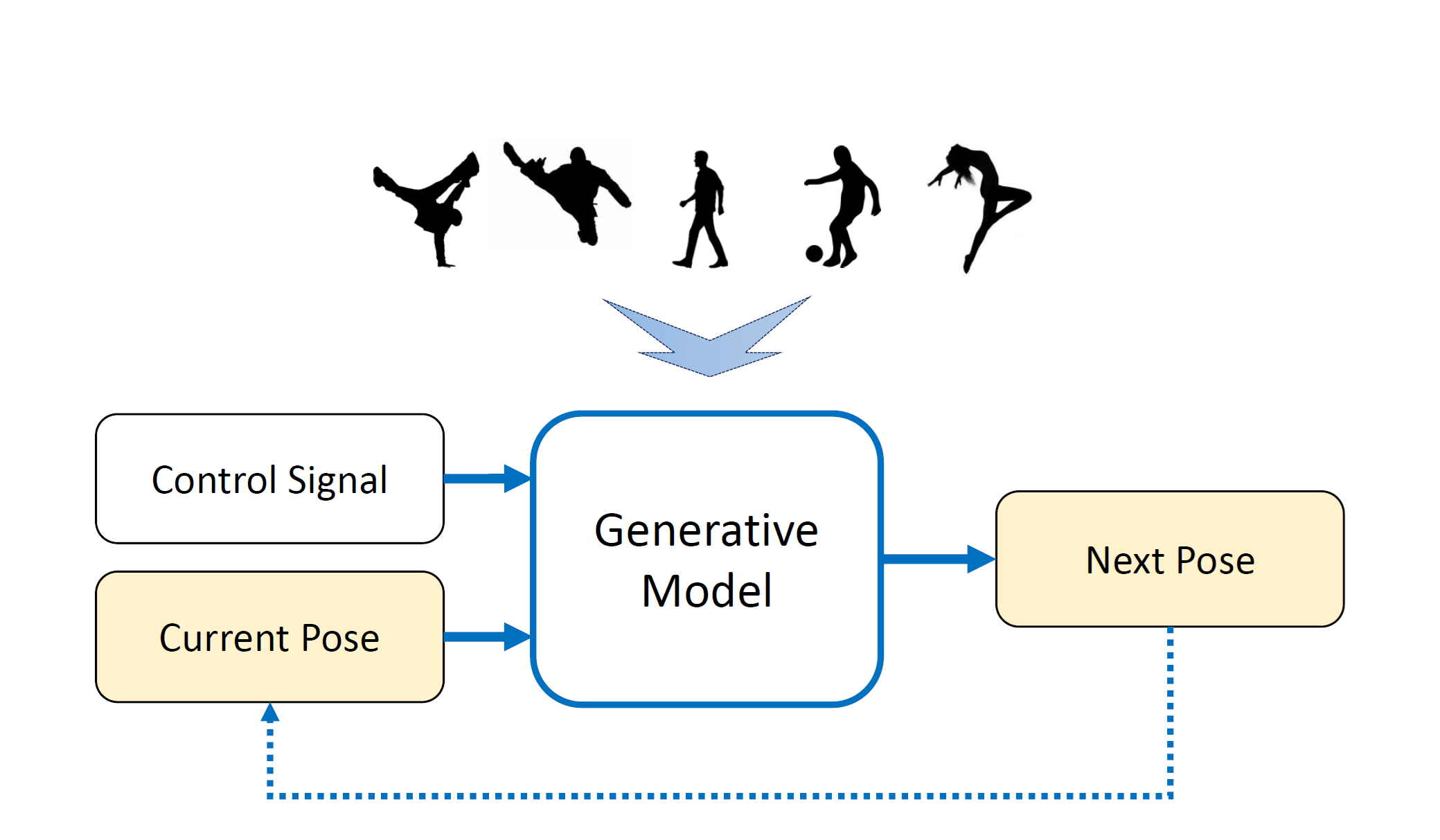
../../_images/animation-character-motion_learning_based1.png
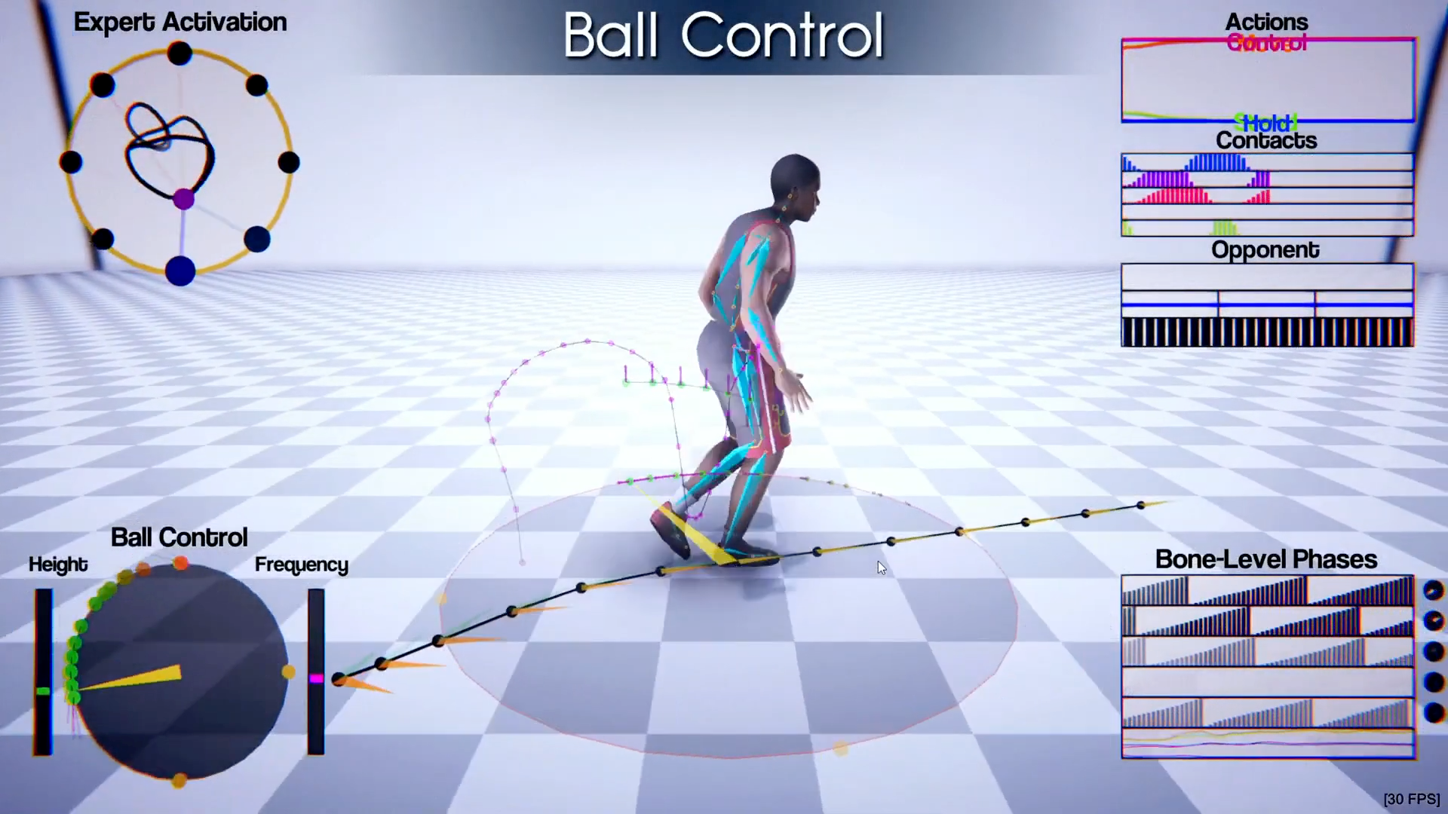
../../_images/animation-character-motion_learning_based2.png

图 20.27 基于学习的方法#