隐式表达

9.3. 隐式表达#

我们此前介绍的网格模型、点云等都是显式的三维表达方式，即，几何信息具体化地直接保存在计算机的数据结构中（点云中的点、网格中的顶点和面）；除了这些显式方法以外，还有一类方法同样能够表达几何形状的表面。这一类方法通过构造一个表示到几何表面最近距离的距离函数，来维护空间每一点的距离信息并得到一个距离场（distance field）。这样的方式并不直接保存表面的位置，而是在距离函数中隐含了关于表面的信息，因此被称为隐式表达（implicit representation）。本节我们将介绍符号距离场的概念，并讨论其在计算机中的实现。

9.3.1. 符号距离场#

无符号距离场（Unsigned Distance Field，UDF）方法维护了一个无符号距离函数（Unsigned Distance Function）表示空间中每一点 \(\mathbf{x}\) 到几何形状 \(M\) 表面的最近距离：

(9.7)#\[ f(\mathbf{x})=\min_{\mathbf{x}'\in \partial M}\|\mathbf{x}-\mathbf{x}'\|_1\,. \]

与之相对，有符号距离场（Signed Distance Field，SDF）方法采用有符号距离函数（Signed Distance Function），不仅表示空间中每一点 \(\mathbf{x}\) 到几何形状 \(M\) 表面的最近距离，还通过正负号对其在 \(M\) 的内部和外部进行了区分：

(9.8)#\[\begin{split} f(\mathbf{x})=\left\{\begin{aligned} -\min_{\mathbf{x}'\in \partial M}\|\mathbf{x}-\mathbf{x}'\|_2&&\text{if }x\in M\,,\\ \min_{\mathbf{x}'\in \partial M}\|\mathbf{x}-\mathbf{x}'\|_2&&\text{if }x\notin M\,. \end{aligned}\right. \end{split}\]

重要

有符号距离场并没有规定符号在形状内部取负值还是在外部取负值，在数学领域，许多情况下倾向于规定在外部取负值。但在可视计算领域，有符号距离函数往往在形状内部取负值。

9.3.2. 符号距离函数的性质#

在可视计算领域，无论是哪种符号距离函数，其定义都基于欧几里得空间距离，因此只要形状 \(M\) 具有分段光滑边界，则符号距离函数几乎处处可微，且其梯度满足程函方程（eikonal equation）：

(9.9)#\[ \|\nabla f\|_2=1 \]

特别地，对于有符号距离函数，其在表面处的梯度方向与表面的法向量方向相同。

9.3.3. 符号距离场的表示方式#

符号距离函数作为连续函数，并不适合直接在计算机中表示。因此，经典的方法采用规则网格来表示符号距离场。具体来说，空间被划分为具有特定分辨率的规则网格，网格顶点上存储了该位置的符号距离函数值。对于网格内部的点，其符号距离函数值可以用周围八个顶点的插值来估计。这种表示方式的优势是实现较为简单，使用格点处的离散值来代替连续、复杂的原函数是常见的离散化手段。然而，其缺陷也较为明显，符号距离函数的表示精度直接受限于规则网格的分辨率。在分辨率较低的情况下，这种方式只能够表示非常简单的形状。

近年来的前沿研究中，另一些方法采用神经网络（neural network）来拟合符号距离函数。神经网络由于可以接受连续的输入并产生相应的输出，相比于经典的离散化表示方法，能够表达更精细的函数变化。有符号距离场与神经网络的结合在计算机图形学和计算机视觉领域中大放异彩，衍生出了神经隐式表面（NeuS）等一系列杰出的工作。

9.3.4. 符号距离场的构建#

许多方法能够将显式的几何形状转化为符号距离场，以便后续的一系列计算处理。这里我们简要介绍两种主要的方法：

9.3.4.1. 快速扫描法#

快速扫描法（Fast Sweep Method，FSM）是一种基于方向扫描策略的高效距离场生成算法，其核心目标是通过有序遍历计算网格顶点到目标几何体的最短距离，并利用扫描传播特性加速计算。以下是其典型流程：

  1. 初始化距离场 设定计算域的三维网格结构，初始化所有顶点的距离值为极大值（表示未计算）； 将目标几何体对应的网格顶点设为“源点”，距离值置零，并标记为活动前沿。

  2. 多方向扫描传播 按照固定顺序对网格进行多轮扫描，每轮沿特定方向遍历网格（例如三维中需进行6次扫描，对应 \(\pm x,\pm y,\pm z\) 方向）； 在单次扫描中，按顺序访问每个网格顶点，根据当前相邻顶点的已知距离值，通过局部更新公式（程函方程的离散形式）计算其到目标的最短距离； 若新计算值小于原值，则更新该顶点距离并标记为活动前沿。

  3. 终止条件 重复多轮方向扫描，直至所有顶点的距离值不再变化（即活动前沿消失）或达到预设迭代次数； 最终输出网格顶点上的精确或近似距离场，表征几何体的空间分布。

快速扫描法通过方向扫描的局部性减少冗余计算，时间复杂度接近线性，同时单次扫描内顶点更新可并行执行，适配GPU加速，因其计算效率与工程实用性，成为几何处理领域的基础算法之一，但其扫描顺序可能导致方向依赖的距离误差，常通过多轮交替扫描或结合其他方法（如快速行进法）进一步优化。

9.3.4.2. 快速步进法#

快速步进法（Fast Marching Method，FMM）是一种基于波前传播思想的高效数值算法，用于求解程函方程并生成距离场，其核心目标是计算空间中每个点到特定几何边界（如曲面、点集）的最短距离，同时确保计算的高效性与精度。算法流程如下：

  1. 初始化距离场 设定计算域的三维网格结构，初始化所有顶点的距离值为极大值（表示未计算）； 将目标几何体对应的网格顶点设为“源点”，距离值置零，并标记为活动前沿； 其余点标记为未计算。

  2. 波前传播迭代 从活动前沿中提取距离值最小的点（类似 Dijkstra 算法，使用优先队列维护），将其标记为已计算； 遍历该点的邻域点（在三维网格中的 6 邻域或 26 邻域），根据程函方程的离散形式更新其距离值； 若新计算的距离值小于原值，则更新邻域点并加入活动前沿。

  3. 终止条件 重复迭代直至所有点均被标记为已计算或达到目标区域，输出全局距离场。

快速步进法避免了波前交叉导致的误差，具有较高精度；同时，其仅向外传播，确保每个点仅计算一次，时间复杂度为 \(O(N\log N)\)。快速步进法支持非均匀网格、各向异性速度场及复杂几何边界，它的工程实用性使其成为几何计算领域的经典方法。

9.3.5. 符号距离场的应用#

符号距离场本身隐式地表示了几何形状，其 0-等值面对应着几何形状的表面。许多方法能够通过对符号距离场求值来计算几何表面的位置。 行进立方体（Marching Cubes）算法就是这样一种方法，它能够从符号距离函数中重建网格模型，被广泛使用于整个几何建模领域。我们在此以规则网格表示的有符号距离场为例，对算法原理与细节进行简要的介绍。

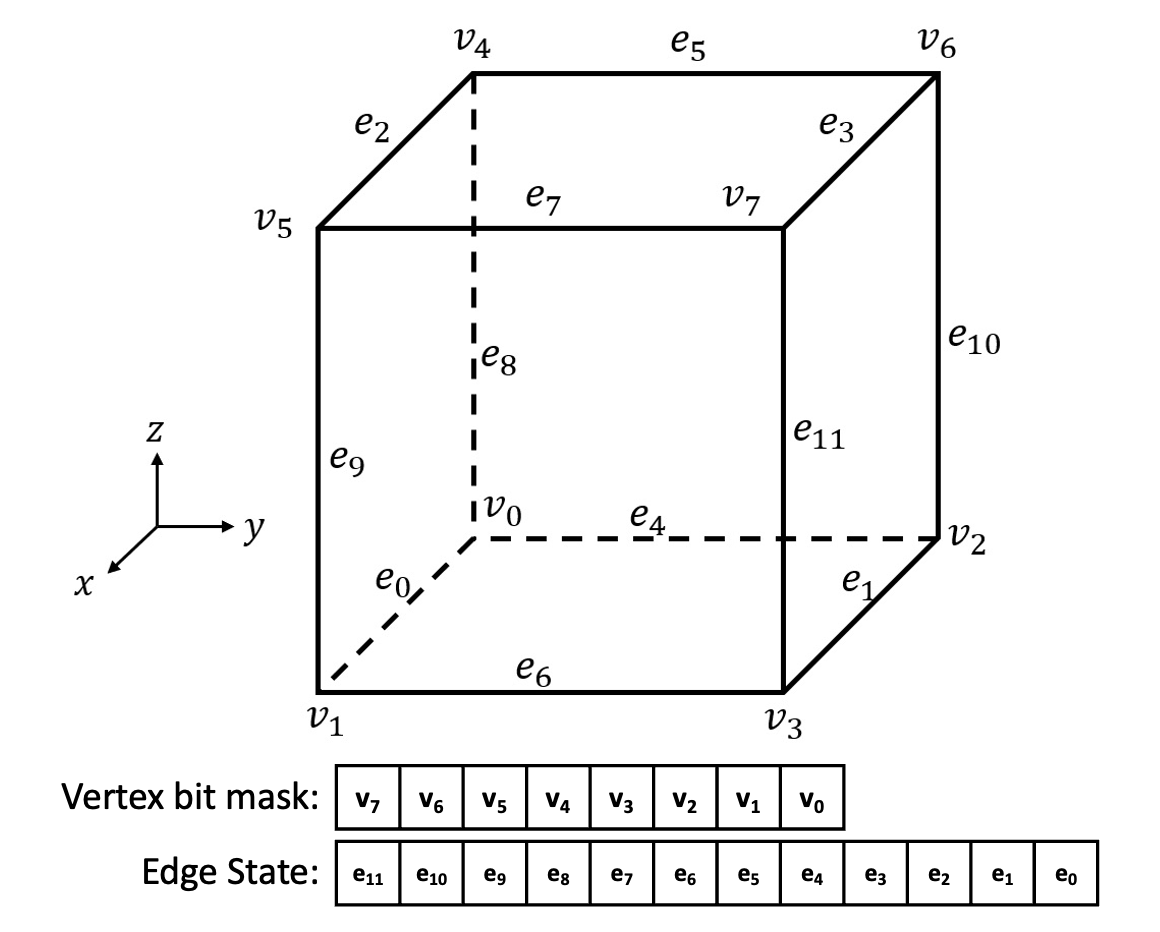
../../_images/marching-cubes-1.png

图 9.10 Marching Cubes 算法。#

../../_images/marching-cubes-2.png

图 9.11 Marching Cubes 中 15 种拓扑关系。#

算法流程大致如下：

  1. 首先，将空间划分为固定大小的立方体体素。然后根据每个顶点的 SDF 值，确定这个顶点在对象的内部还是外部。

  2. 然后，对于每个体素立方体的八个顶点的 SDF 值正负性，我们将其编码成 \(2^8=256\) 种情形并用一个 8-bit 二进制索引表示，如 图 9.10 中，索引（vertex bit mask）的每一位为 \(0\) 或 \(1\) 分别表示该顶点的 SDF 值小于 \(0\) 和大于等于 \(0\)。全部 256 个索引构成了 256 种拓扑关系，并可以根据对称性简化为 15 种；这 15 种拓扑关系通过旋转平移等对称性操作就可以覆盖全部 256 种情形。如 图 9.11 所示。

  3. 算法维护了两个查询表。第一个表根据顶点编码成的索引查询关于边状态的编码（edge state），这是一个 12-bit 的二进制串，其中每一位为 0 或 1 分别表示该边与等值面相交和不相交。根据这些信息可以在立方体的边上生成最终需要的网格顶点；这些网格顶点的位置由该边的两个端点按照 SDF 值插值得到，即该边与等值面相交的估计位置。例如边的两个端点分别具有 \(\mathbf{p}_1,\mathbf{p}_2\) 的位置属性和 \(v_1,v_2\) 的SDF值时，通过下式估计等值面（假设等值面处 SDF 值为 \(v^*\)）与边的交点，生成所需的顶点网格：

    (9.10)#\[ \mathbf{p}^*=\frac{v_2-v^*}{v_2-v_1}\mathbf{p}_1+\frac{v^*-v_1}{v_2-v_1}\mathbf{p}_2\,. \]

提示

然而，不那么显然的一点是，行进立方体算法的 15 种拓扑关系中实际上存在一些歧义性（ambiguity）；行进四面体（Marching Tetrahedrons）算法通过将规则网格替换为四面体网格，对此提出了改进。