贝塞尔曲线

6.3. 贝塞尔曲线#

../../_images/Bezier_curve.svg

图 6.14 贝塞尔曲线[1]#

贝塞尔曲线（Bézier curve） 是图形学、工程学、设计学等领域最常用的一类高阶曲线，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）在20世纪60年代为汽车工业开发。贝塞尔曲线的定义非常简单，并且具有很好的几何性质。

6.3.1. 定义#

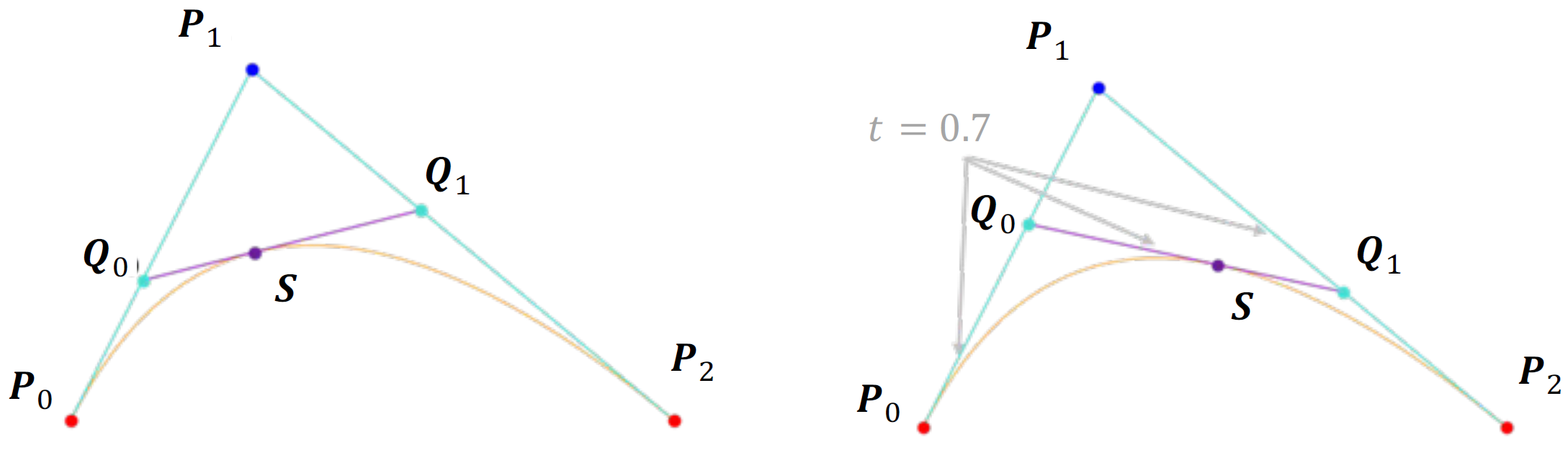
../../_images/dec.png

图 6.15 德卡斯特里奥算法构造二阶贝塞尔曲线#

我们先来看如何构造二阶贝塞尔曲线。如图 6.15 所示，我们有三个控制点 \(\mathbf{P}_0, \mathbf{P}_1, \mathbf{P}_2\)，通过两轮线性插值得到曲线。第一轮，由参数 \(t\) 对 \(\overrightarrow{\mathbf P_0\mathbf P_1}\) 和 \(\overrightarrow{\mathbf P_1\mathbf P_2}\) 分别做线性插值，得到由同一个参数 \(t\) 分别在上述两条一阶曲线上对应的点：

(6.18)#\[\begin{split} \begin{align} \mathbf Q_0&=\mathrm{lerp}(\mathbf P_0, \mathbf P_1, t)=(1-t)\mathbf P_0+t\mathbf P_1\text{,}\\ \mathbf Q_1&=\mathrm{lerp}(\mathbf P_1, \mathbf P_2, t)=(1-t)\mathbf P_1+t\mathbf P_2 \end{align} \end{split}\]

第二轮，通过对 \(\overrightarrow{\mathbf Q_0\mathbf Q_1}\) 做线性插值，得到同一个参数 \(t\) 对应的点：

(6.19)#\[ \mathbf S=\mathrm{lerp}(\mathbf Q_0, \mathbf Q_1, t)=(1-t)\mathbf Q_0+t\mathbf Q_1 \]

令 \(t\) 遍历 \([0,1]\) 取值范围，即得到由 \(\mathbf P_0, \mathbf P_1, \mathbf P_2\) 控制的二阶贝塞尔曲线。这个算法称为 德卡斯特里奥算法（de Casteljau’s algorithm），效率较高，编程方便且数值稳定性较好，因而得到了广泛的使用。类似地，我们同样可以定义三阶贝塞尔曲线。三阶贝塞尔曲线由四个控制点给出，可以通过三轮线性插值得到，如图 6.16 所示。

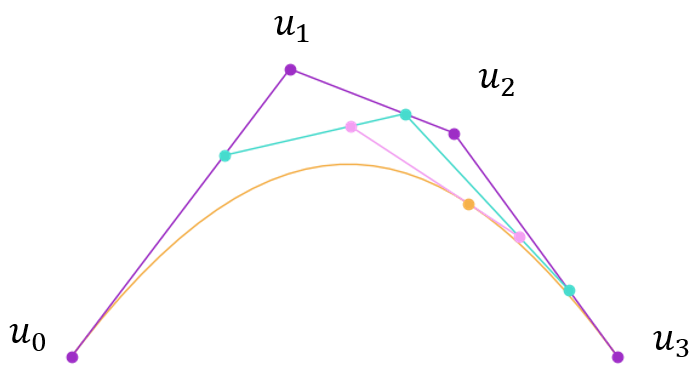
../../_images/cubic_bezier.png

图 6.16 德卡斯特里奥算法构造三阶贝塞尔曲线#

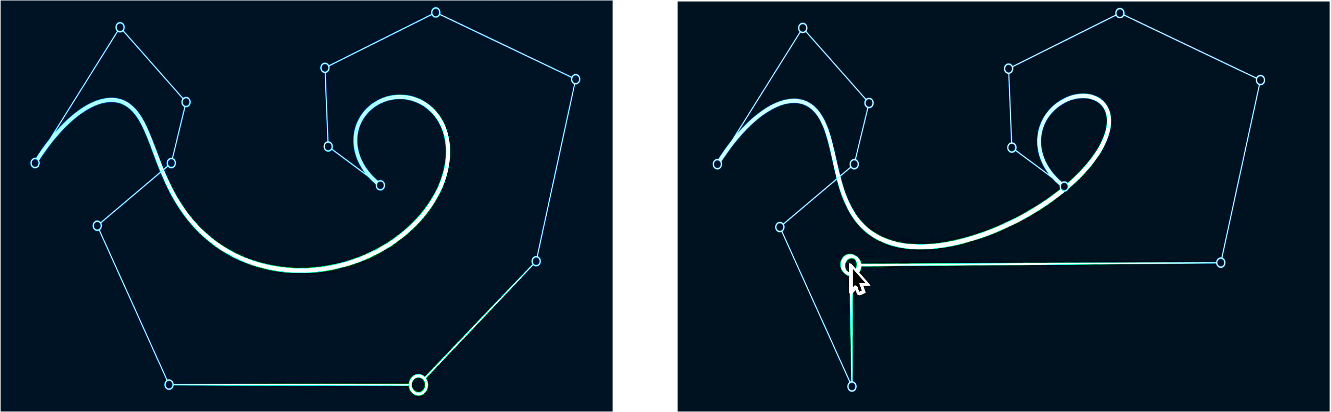
进而我们可以将贝塞尔曲线的阶数推广到任意高，\(n\) 阶贝塞尔曲线由 \(n+1\) 个控制点给出。但贝塞尔曲线每个控制点对曲线的影响不是局部的，如图 6.17 所示，因此随着阶数的提高，通过控制点对曲线形状做出有效控制的难度也随之提高。解决方法就是使用分段的低阶贝塞尔函数，也就是贝塞尔样条（Bézier spline），如图 6.18 所示。

../../_images/bezier-nonlocal-2.png

图 6.17 一条十二阶贝塞尔曲线，挪动其中一个顶点会改变整条曲线的形状[2]#

../../_images/Beziergon.svg

图 6.18 一条贝塞尔样条曲线#

由上述构造方法我们可以求出贝塞尔曲线的数学表达式。以二阶贝塞尔曲线为例，结合公式 (6.18) 和公式 (6.19) 我们可以得到曲线的表达式：

(6.20)#\[\begin{split} \begin{align} \mathbf S &= (1-t) \mathbf Q_0 + t \mathbf Q_1\\ &= (1-t)( (1-t) \mathbf P_0+ t \mathbf P_1) + t((1-t) \mathbf P_1 + t\mathbf P_2)\\ &= (1-t)^2 \mathbf P_0 + 2t(1-t) \mathbf P_1 + t^2 \mathbf P_2\text{.} \end{align} \end{split}\]

不难发现，上式中对各控制点的权重系数正是二项式 \((t+(1-t))^2\) 展开后的各项。更一般地，\(n\) 阶贝塞尔曲线的数学表达式为：

(6.21)#\[ \mathbf S(t) = \sum_{k=0}^n B_{n,k}(t) \mathbf P_k = \sum_{k=0}^n \binom{n}{k} (1-t)^k t^{n-k} \mathbf P_k \]

其中系数多项式为

(6.22)#\[ B_{n,k}(t)=\binom{n}{k} (1-t)^k t^{n-k} \]

被称为 \(n\) 阶伯恩斯坦多项式（Bernstein polynomials）。

6.3.2. 性质#

首先，我们考察一条贝塞尔曲线的端点。根据公式 (6.21) 可得 \(\mathbf S(0)=\mathbf P_0,\,\mathbf S(1)=\mathbf P_{n}\)，即，贝塞尔曲线必然经过两端控制点，但一般来说不会经过中间其余控制点。公式 (6.21) 对参数\(t\)求导可得：

(6.23)#\[\begin{split} \begin{align} \mathbf S'(t) &= \frac{\mathrm d}{\mathrm d t}\sum_{k=0}^n B_{n,k}(t) \mathbf P_k\notag\\ &=n\sum_{k=0}^{n-1} B_{n-1,k}(t) (\mathbf P_{k+1}-\mathbf P_{k}) \end{align} \end{split}\]

其中用到了伯恩斯坦多项式的导数性质，可以从公式 (6.22) 直接推导，也可以通过公式 (6.20) 来验证。代入两个端点的值，我们有：

(6.24)#\[\begin{split} \begin{align} \mathbf S'(0) &= n(\mathbf P_1 - \mathbf P_0), \\ \mathbf S'(1) &= n(\mathbf P_n - \mathbf P_{n-1}) \end{align} \end{split}\]

可见，端点处切线分别沿着 \(\overrightarrow{\mathbf P_0 \mathbf P_1}\) 连线和 \(\overrightarrow{\mathbf P_n \mathbf P_{n-1}}\) 连线的方向。因此，如果我们希望两条相连的贝塞尔曲线在连接点处光滑过渡，只需要施加边界条件令它们在公共端点两旁的控制点在同一条直线上即可，如图 6.18 所示。这一条件保证了 \(G^1\) 光滑，而若要达到 \(C^1\) 光滑，则还需要令 \(\|\mathbf P_n-\mathbf P_{n-1}\| = \|\mathbf P_{n+1} - \mathbf P_{n}\|\)，即，约束加强为 \(\mathbf P_n-\mathbf P_{n-1} = \mathbf P_{n+1} - \mathbf P_{n}\)。因此，一条三阶贝塞尔曲线的四个控制点刚好可以让我们自由控制两端的切线，这也是我们一般使用三阶而不是二阶贝塞尔曲线的原因。

贝塞尔曲线另一条重要的性质是凸包性质（convex-hull property）。由于贝塞尔曲线的权重均非负，且曲线上任意一点关于控制点的权重和为 \(1\)，故而由凸包的定义可知，贝塞尔曲线被包围在由它所有控制点组成的最小凸包当中，即控制点凸包给出了一个贝塞尔曲线的包围盒（尽管不是最小包围盒）。这个性质能帮助我们很好地规划贝塞尔曲线的路径。比如在规划虚拟场景中相机的轨迹时，我们可以通过规划控制点的凸包，避免相机走到我们不想其到达的位置。

../../_images/hull.jpg

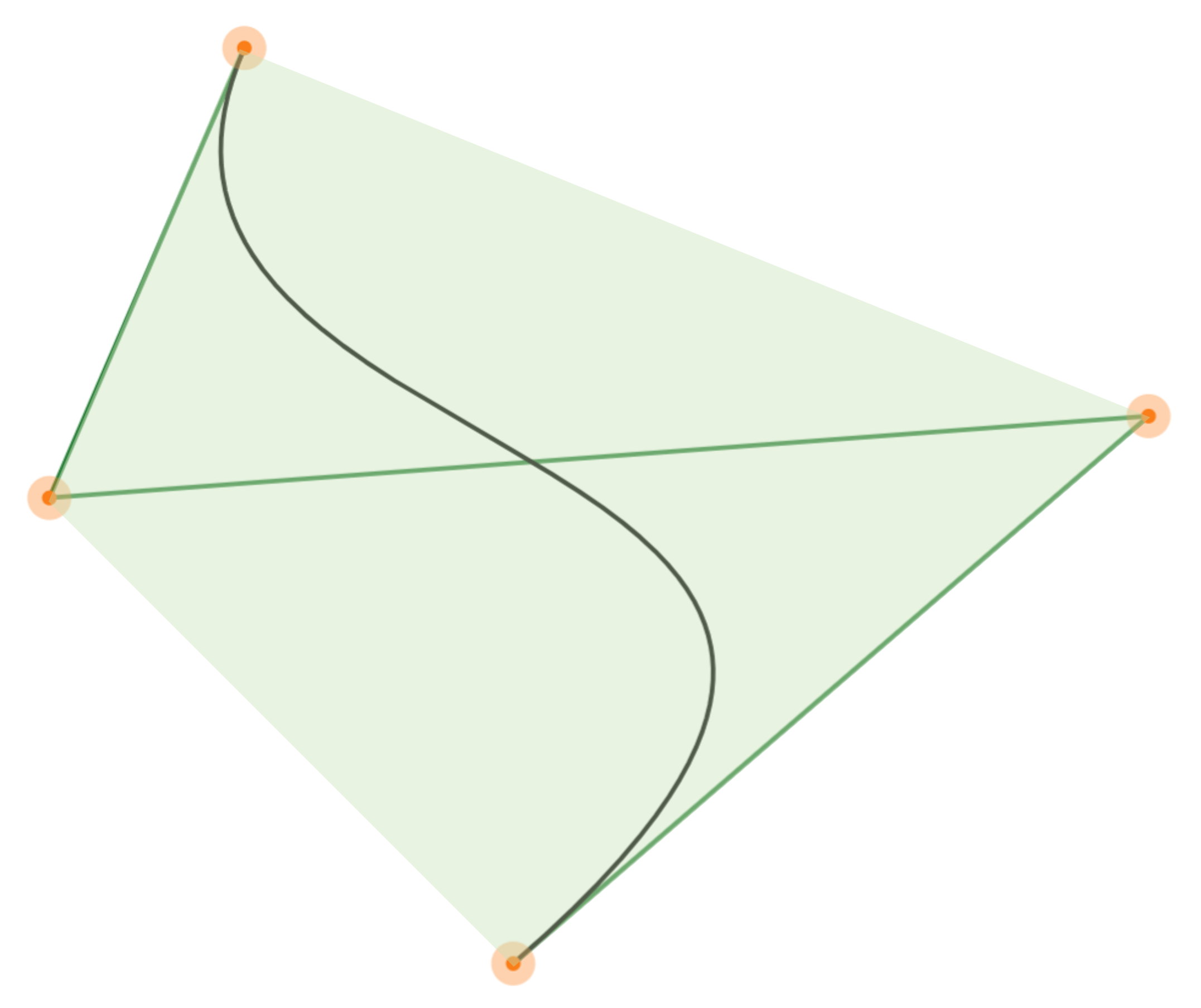
图 6.19 贝塞尔曲线和对应控制点的凸包#