21.1. 弹簧质点系统#

21.1.1. 物理模型#

在模拟一个物理世界之前，我们首先需要理解它的物理原理，而在仿真当中，我们最关心的就是物体的运动情况。对于日常生活中宏观低速的物体，其运动规律就是我们所熟知的牛顿第二定律——力是物体改变运动状态的原因。对于一个质量为 \(m\) 的质点，假设其位置向量 \(\boldsymbol x\)，受力 \(\boldsymbol f\)，则它的运动学方程为

(21.1)#\[ \boldsymbol f=m\ddot{\boldsymbol x}。 \]

这里，我们常用 \(\dot{\boldsymbol{x}}\) 和 \(\ddot{\boldsymbol{x}}\) 表示位置对时间求一阶导和二阶导得到的梯度向量（有时也分别记为 \(\boldsymbol v\) 和 \(\boldsymbol a\)），即速度和加速度。我们关心的物体的受力 \(\boldsymbol f\) 可以是这个世界上具有的任何力，包括重力、弹性力、浮力、表面张力、磁力等等。

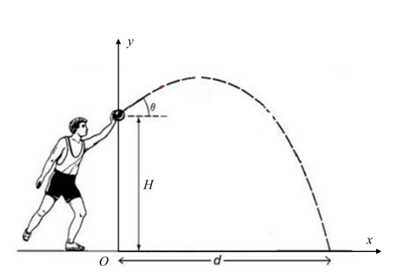
../../_images/animation-elastomers-simple_example.png — 图 21.1 单一粒子运动的例子#

我们考虑一个最简单的例子：粒子以一定初速度被抛出，在重力作用下运动直至落地。由于粒子的运动轨迹一定在一个平面内，我们设 \(x\) 轴正方向为粒子的水平运动方向，\(y\) 轴正方向为竖直朝上（如图 21.1 所示），原点在粒子初始位置的正下方；另外设粒子初始高度为 \(H\)，初始速度大小为 \(v_0\)，方向与 \(x\) 轴夹角为 \(\theta\)。这个粒子的运动十分简单，它只受到一个向下重力，即

\[\begin{split} \boldsymbol f=\begin{bmatrix}0\\-mg\end{bmatrix}， \end{split}\]

其中 \(m\) 为粒子的质量。根据式 (21.1) 可得粒子的加速度

\[\begin{split} \ddot{\boldsymbol x}=\begin{bmatrix}0\\-g\end{bmatrix}。 \end{split}\]

粒子的速度可由初速度加上加速度的时间积分得到：

\[\begin{split} \boldsymbol x=\begin{bmatrix}0\\H\end{bmatrix}+\int_0^t\dot{\boldsymbol x}\mathrm d\tau=\begin{bmatrix}(v_0\cos\theta)t\\H+(v_0\sin\theta)t-\frac 12gt^2\end{bmatrix}。 \end{split}\]

21.1.2. 物理模拟#

对上一节的例子，我们已经完全了解了粒子的全部运动，但是这个例子实在过于简单——整个场景中只有一个粒子，并且只受一个力——以至于它难以代表一般性的情况。在一般的物理模拟场景中，一块连续的材料 (如一个弹性体、一单位体积的流体或是一片布料) 包含无穷多粒子，并且往往会存在多个外力以及粒子之间的十分复杂的内力。这个时候，系统往往不再存在解析解，所以我们就退而求其次，寻求一个尽可能接近物理真实情况的数值解。物理模拟（或物理仿真）就是寻求数值解的过程。

为了进行物理模拟，我们首先要做的是将一个在空间上连续的物体进行空间离散化，设计适当的数据结构以存储它的拓扑结构及运动状态。然后根据它所遵循的运动规律（运动学方程），在给定初始状态的前提下，对它的运动进行步进求解。这个过程大致如图 21.2 所示，我们将依次介绍它的三个组成，即空间离散化、时间离散化、数值求解。

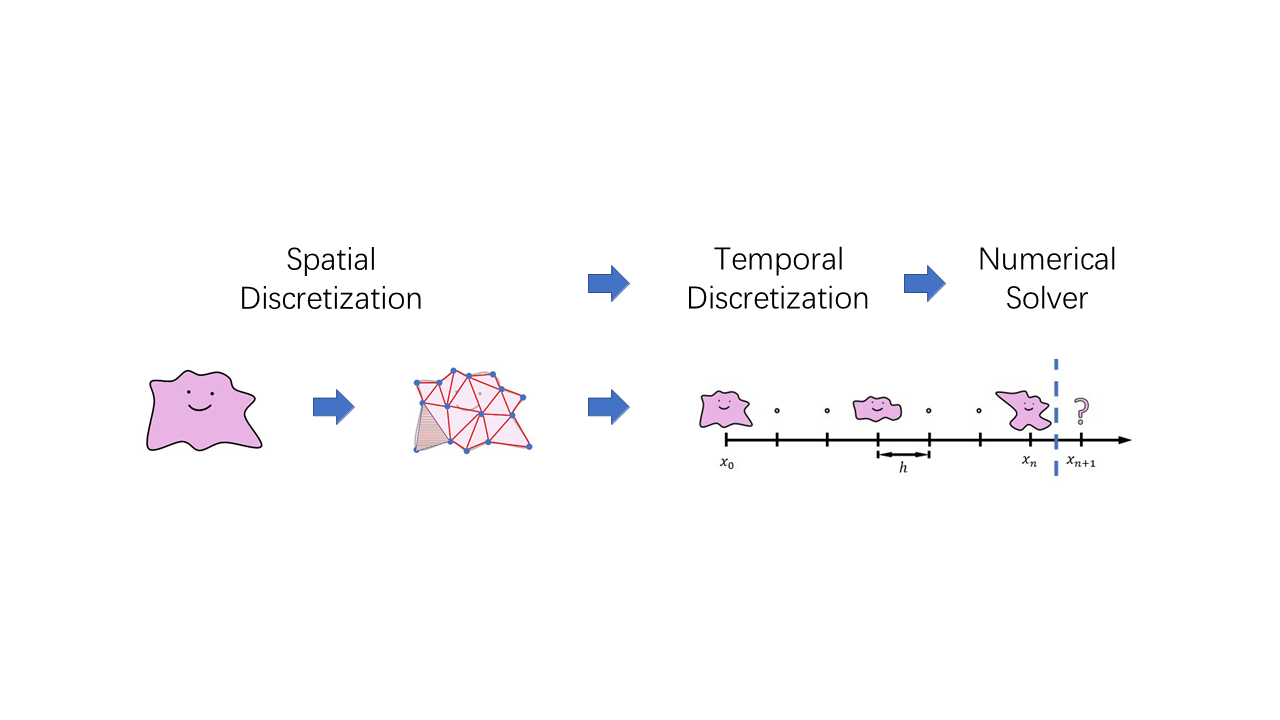
../../_images/animation-elastomers-pipeline.png — 图 21.2 物理仿真的过程#

21.1.3. 空间离散化#

质点具有质量，会因力的作用改变运动状态，但没有空间体积和形状，是物理学中的一种理想化模型。单个质点的状态是由它的位置和速度确定的。而为了在已知状态的基础上模拟出质点的运动过程，我们还需要通过受力和质量计算出它的加速度。进一步地，一个由多个质点组成的质点系统，其数据结构可以简单地设计成一个质点的列表，如图 21.3 所示。

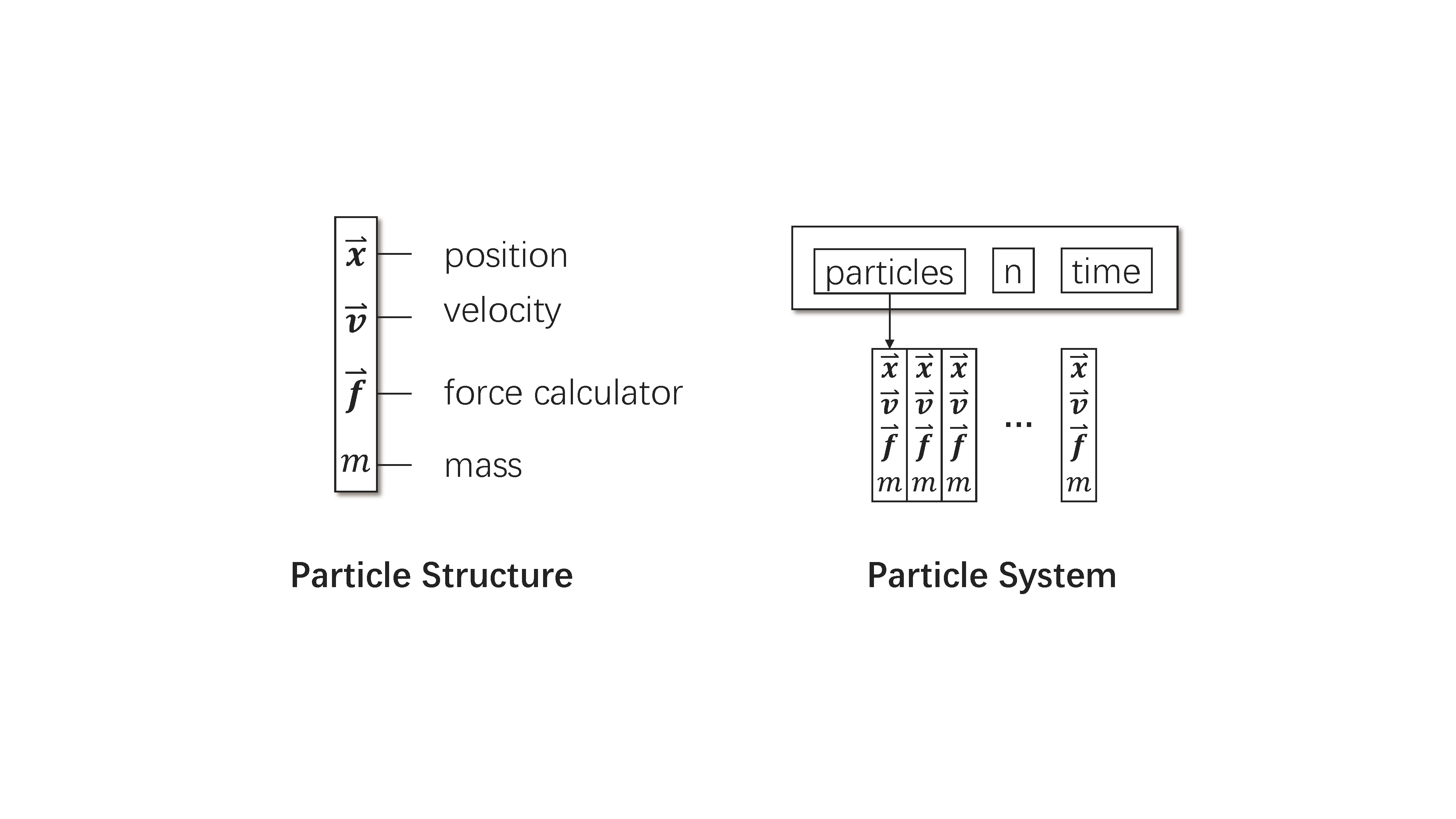
../../_images/animation-elastomers-particle.png — 图 21.3 质点系统的组成[1]#

另外，弹簧质点系统的能量由忽略质量的弹簧提供，为了简便，我们可以额外假设弹簧无阻尼，即弹簧的弹力和弹性势能只是两端质点位置的函数，与质点速度和时间无关。一个三维弹簧的弹性势能，具有以下的特点：

撤去所有外力后弹簧回到原长，即原长对应单根弹簧弹性势能的最小值点；
刚性运动（平移、旋转）不改变弹性势能；
弹性势能只依赖于所连接质点的位置（对于无阻尼弹簧）。

对于一根连接质点 \(i,j\) 的弹簧，设其原长为 \(l_{ij}\)，劲度系数为 \(k_{ij}\)，前面已经提到两质点的位置分别为 \(\boldsymbol x_i,\boldsymbol x_j\)，取其弹性势能为

(21.2)#\[ E_{ij}=\frac 12k_{ij}\left(\|\boldsymbol x_j-\boldsymbol x_i\|-l_{ij}\right)^2。 \]

对 \(E_{ij}\) 关于 \(\boldsymbol x_i\) 求负梯度可得 \(i\) 受该弹簧的弹力 \(\boldsymbol f_{ij}\)，同理关于 \(\boldsymbol x_j\) 求负梯度可得 \(\boldsymbol f_{ji}\)，\(\boldsymbol f_{ij},\boldsymbol f_{ji}\) 的表达式如下：

(21.3)#\[\begin{split} \boldsymbol{f}_{ij}&=-\nabla_iE_{ij}=k_{ij}\left(\|\boldsymbol x_j-\boldsymbol x_i\|-l_{ij}\right)\frac{\boldsymbol{x}_j-\boldsymbol{x}_i}{\|\boldsymbol x_j-\boldsymbol x_i\|}=k_{ij}\left(\|\boldsymbol x_j-\boldsymbol x_i\|-l_{ij}\right)\boldsymbol{n}_{ij}，\\ \boldsymbol{f}_{ji}&=-\nabla_jE_{ij}=-\boldsymbol{f}_{ij}， \end{split}\]

其中 \(\boldsymbol{n}_{ij}\) 为从质点 \(i\) 指向 \(j\) 方向的单位向量。

由此我们可以得到一个质点 \(i\) 所受的合力：

(21.4)#\[ \boldsymbol f_i=\sum_{j\in N(i)}\boldsymbol f_{ij}+\boldsymbol f_i^{\mathrm{ext}}， \]

其中 \(N(i)\) 表示所有和 \(i\) 之间有弹簧连接的质点的集合；\(\boldsymbol f_i^{\mathrm{ext}}\) 表示质点 \(i\) 所受的外力，如重力，外力与位置无关，一般可以提前计算出来，我们在后面就会看到为什么要将外力写成额外的一项。

21.1.4. 时间离散化#

物体运动状态随时间连续变化，因此在时间维度上同样需要进行离散化。这意味着对式 (21.1) 的微分方程进行离散化。一般来说，我们在时间区间上均匀采样，物理动画的帧率即由采样的时间间隔 \(h\)（通常也称为时间步长，单位秒，帧率即为时间步长的倒数）决定。当已知当前物体的状态 (如质点系统中每个质点的位置和速度)，可以计算出相应的受力情况，因此可以通过时间积分求出下一采样时刻的物体状态。我们记 \(t\) 时刻的位置和速度向量为 \(\boldsymbol{x}(t)\) 和 \(\boldsymbol{v}(t)\)，并简记第 \(k\) 次采样时刻 \(t_k\) 的位置与速度向量为 \(\boldsymbol{x}^k=\boldsymbol{x}(t_k)\) 和 \(\boldsymbol{v}^k=\boldsymbol{v}(t_k)\)，对于一个 \(n\) 个质点组成的质点系统而言，分别为 \(n\) 个质点的位置和速度的堆叠向量，\(\boldsymbol{x}^k,\boldsymbol{v}^k\in\mathbb R^{3n}\)，即

\[\begin{split} \boldsymbol{x}^k &= \begin{pmatrix} \boldsymbol{x}_1(t_k)\\ \boldsymbol{x}_2(t_k)\\ \vdots\\ \boldsymbol{x}_n(t_k) \end{pmatrix}，\\ \dot{\boldsymbol{x}}^k &= \boldsymbol{v}^k= \begin{pmatrix} \boldsymbol{v}_1(t_k)\\ \boldsymbol{v}_2(t_k)\\ \vdots\\ \boldsymbol{v}_n(t_k) \end{pmatrix}。 \end{split}\]

递进一个时间步意味着物体状态从 \(t_k\) 时刻到 \(t_{k+1}\) 时刻的更新，具体来说，就是基于牛顿第二定律的离散化表达，计算出下一时刻物体的状态：

(21.5)#\[\begin{split} \boldsymbol{x}^{k+1}&=\boldsymbol{x}^k+\int_{t_k}^{t_{k+1}}\boldsymbol{v}(t)\mathrm dt， \\ \boldsymbol{v}^{k+1}&=\boldsymbol{v}^k+\boldsymbol{M}^{-1}\int_{t_k}^{t_{k+1}}\boldsymbol{f}(t, \boldsymbol{x}(t), \boldsymbol{v}(t))\mathrm dt， \end{split}\]

其中，式 (21.5) 中的标量质量 \(m\) 需要处理成质量矩阵 \(\boldsymbol{M}\)，对于质点系统来说，可以取为对角矩阵，这也便于并行求解。

因此，给定系统的初始位置 \(\boldsymbol{x}_0\) 和初始速度 \(\boldsymbol{v}_0\)，通过上式循环迭代，理论上就可以依次求出后续每个采样时刻的系统状态，从而得到一段物理动画。故剩下的任务是计算式 (21.5) 中的时间积分，接下来介绍两种典型的计算方法：显式欧拉积分（explicit/forward Euler）和隐式欧拉积分（implicit/backward Euler）。

21.1.4.1. 显式欧拉积分#

在较为复杂的场景中，式 (21.5) 中的积分项可能不存在解析表达，好在积分区间 \([t_k,t_{k+1}]\) 比较小，所以我们可以用简单的形式近似这个积分的值。最简单的方式就是用每个时间步刚开始的值去近似这个时间步内任意时刻的值，于是式 (21.5) 转化成

(21.6)#\[ \boldsymbol{x}^{k+1}=\boldsymbol{x}^k+h\boldsymbol{v}^k \]

(21.7)#\[ \boldsymbol{v}^{k+1}=\boldsymbol{v}^k+h\boldsymbol{M}^{-1}\boldsymbol{f}(\boldsymbol{x}^k) \]

这就是显示欧拉积分，只需要根据已知的位置和速度状态就可以直接计算出下一时刻的状态，计算过程十分简便。每个时间步内的计算步骤如下所示：

利用当前时刻的位置 \(\boldsymbol x^k\) 使用式 (21.3) 计算每个弹簧的力，然后用式 (21.4) 计算每个质点的受力；
利用当前时刻速度 \(\boldsymbol v^k\) 使用式 (21.6) 更新位置；
利用前面算好的每个质点的受力使用式 (21.7) 更新速度。

但是，显示时间积分有稳定性差的缺点。我们不妨想象一个质点被一根弹簧吊在天花板上的情形，如图 21.4 最左一列所示，假设质点初始时有一个向下的速度，质点在重力和弹簧拉力的作用下在水平虚线处达到平衡。若时间步很大，那么由于质点具有一定初速度，在第一个时间步过后质点就会越过平衡位置并且超出很多；那么在下一个时间步开始时弹簧的拉力会大于重力，导致质点的速度变成向上，且速度大小比初始速度更快，于是经过第二个时间步之后粒子会冲得更高，以此类推。我们可以很明显注意到这个过程中整个系统的能量大大地增加了，所以会导致这个粒子运动速度越来越快、运动幅度越来越大，直至冲出屏幕，或是超出浮点运算范围。

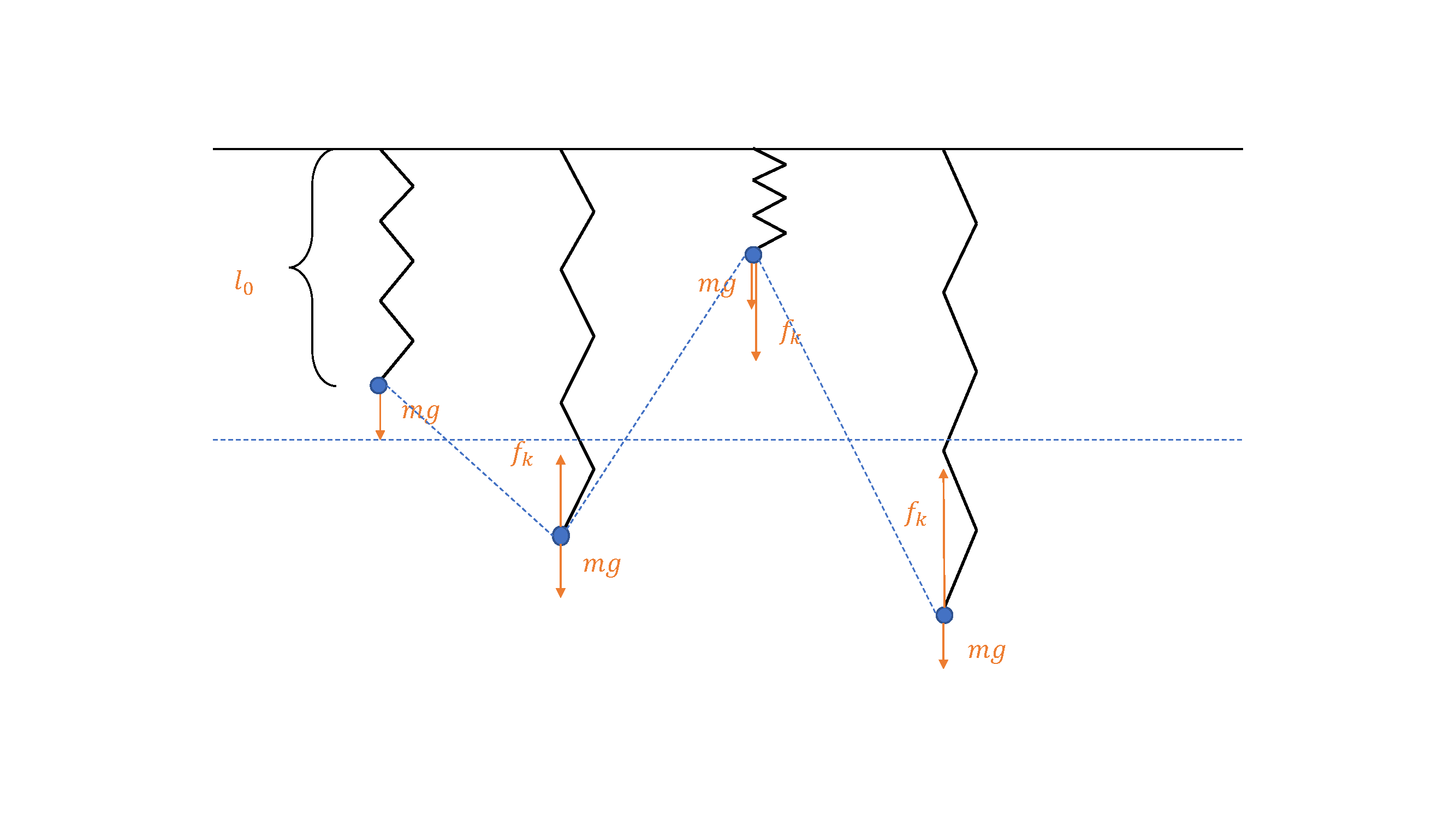
../../_images/animation-elastomers-spring_explode.png — 图 21.4 在大时间步下显示时间积分炸掉的例子#

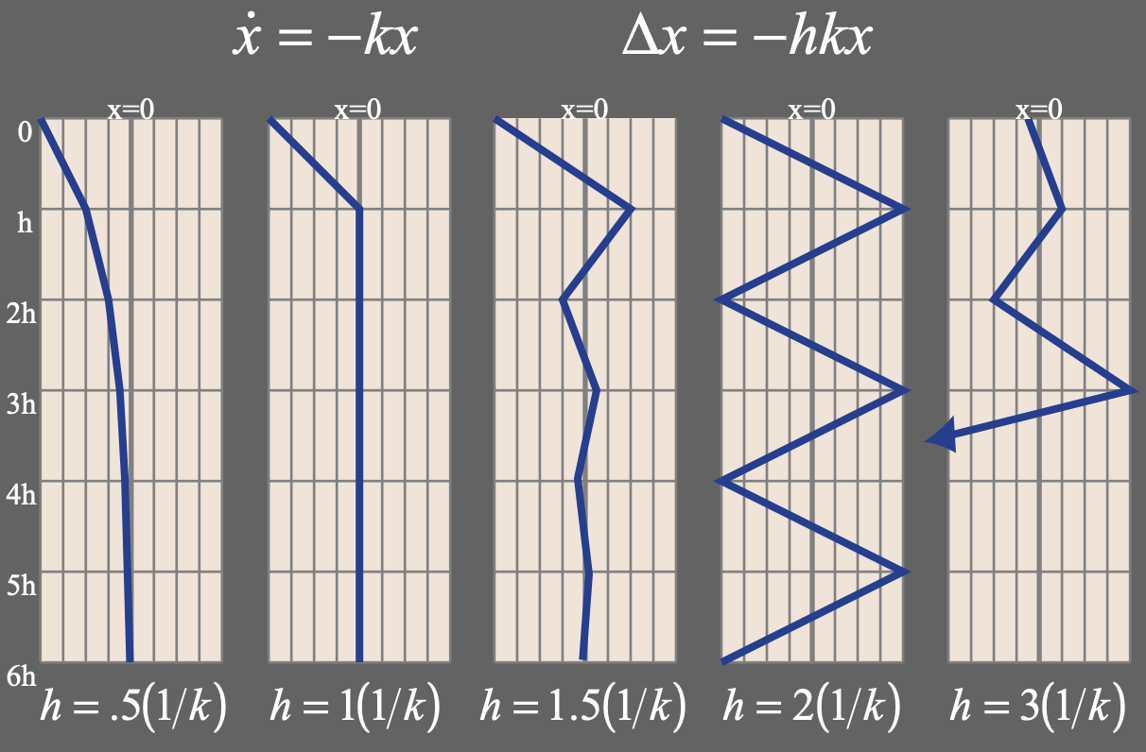
../../_images/animation-elastomers-explicit_timestep.png — 图 21.5 显式欧拉积分在不同时间步大小情况下的表现。微分方程 \(\dot x=-kx\) 存在解析解 \(x(t)=ce^{-kt}\)，其中 \(c\) 为任意常数，带入初始条件 \(x(0)=-1\) 可得 \(c=-1\)。在时间步长足够小的时候 (最左侧)，可以模拟出 \(x\) 随 \(t\) 指数衰减至 \(0\) 的趋势，但随着时间步长的增大，模拟结果依次变得不准确、出现震荡、不收敛、指数级发散。#

当然，解决不稳定的方法是存在的，一个最简单的方法就是减小时间步长。图 21.5 展示了在利用显式欧拉积分解微分方程 \(\dot{x}=-kx\) 时，不同时间步长对结果的影响。可以看到在左侧时间步长很小的情况下能够稳定模拟，但是随着时间步长的加大，结果会变得不准确，甚至炸掉。减小时间步是一个很有效的解决方法，但是这会大大增加需要模拟的时间步的数量；并且如果模拟的场景中物体速度越快，时间步长就需要越小才能够稳定，这会极大增加运算量。想要真正解决稳定性问题，我们还需借助另外一种时间积分格式。

21.1.4.2. 隐式欧拉积分#

在隐式欧拉积分中，我们将式 (21.5) 转化成

(21.8)#\[ \boldsymbol{x}^{k+1}=\boldsymbol{x}^k+h\boldsymbol{v}^{k+1}， \]

(21.9)#\[ \boldsymbol{v}^{k+1}=\boldsymbol{v}^k+h\boldsymbol{M}^{-1}\boldsymbol{f}(\boldsymbol{x}^{k+1})。 \]

可以看出，它和显式欧拉积分的区别在于，隐式欧拉法选取 \(t_{k+1}\) 时刻 (而非 \(t_k\) 时刻) 的位置和速度来近似整个时间步内的值。

隐式欧拉法中我们无法直接计算 \(\boldsymbol{x}^{k+1}\) 和 \(\boldsymbol{v}^{k+1}\)，而是需要求解方程组。将式 (21.9) 代入到式 (21.8) 中，得到

(21.10)#\[ \boldsymbol{x}^{k+1}=\boldsymbol{x}^k+h\boldsymbol{v}^k+h^2\boldsymbol{M}^{-1}\boldsymbol{f}(\boldsymbol{x}^{k+1})。 \]

然后我们将 \(\boldsymbol f(\boldsymbol x^{k+1})\) 分成内力和外力两部分：

\[ \boldsymbol{f}(\boldsymbol{x}^{k+1})=\boldsymbol{f}_{\mathrm{int}}(\boldsymbol{x}^{k+1})+\boldsymbol{f}_{\mathrm{ext}}。 \]

前面已经提到过，\(\boldsymbol f_{\mathrm{ext}}\) 与位置无关，可以视为已知量，那么式 (21.10) 变为

\[ \boldsymbol x^{k+1}=(\boldsymbol x^k+h\boldsymbol v^k+h^2\boldsymbol M^{-1}\boldsymbol f_{\mathrm{ext}})+h^2\boldsymbol M^{-1}\boldsymbol f_{\mathrm{int}}(\boldsymbol x^{k+1})， \]

等号右边前半部分都是已知量，记 \(\boldsymbol y^k=\boldsymbol x^k+h\boldsymbol v^k+h^2\boldsymbol M^{-1}\boldsymbol f_{\mathrm{ext}}\)，那么我们要求解的是如下所示的一个关于 \(\boldsymbol x^{k+1}\) 的方程组：

\[ \boldsymbol x^{k+1}-\boldsymbol y^k-h^2\boldsymbol M^{-1}\boldsymbol f_{\mathrm{int}}(\boldsymbol x^{k+1})=\boldsymbol x^{k+1}-\boldsymbol y^k+h^2\boldsymbol M^{-1}\frac{\partial E}{\partial\boldsymbol x}(\boldsymbol x^{k+1})=0。 \]

它等价于求解如下的优化问题（读者可以利用目标函数关于 \(\boldsymbol x\) 的梯度等于 \(\boldsymbol 0\) 证明等价性）：

\[ \boldsymbol x^{k+1}=\mathop{\arg\min}\limits_{\boldsymbol x}\frac{1}{2h^2}\|\boldsymbol x-\boldsymbol y^k\|^2_{\boldsymbol M}+E(\boldsymbol x)， \]

其中 \(\|\boldsymbol r\|^2_{\boldsymbol M}=\boldsymbol r^\top\boldsymbol M\boldsymbol r\)。这就是说，隐式欧拉积分等价于求解一个能量最小化问题，这个能量包含惯性项（inertia）\(\frac{1}{2h^2}\|\boldsymbol x-\boldsymbol y^k\|^2_{\boldsymbol M}\) 和弹性项（elasticity）\(E(\boldsymbol x)\)（还记得式 (21.2) 定义的弹性势能吗？\(E(\boldsymbol x)\) 就定义为每个弹簧势能之和 \(E(\boldsymbol x)=\sum_{(i,j)}E_{ij}\)），这也就是为什么我们说隐式欧拉法可以解决稳定性问题——它可以在任意长的时间步下稳定，因为它时刻保证系统的能量最小化。

所以在很多情况下，我们会采用隐式欧拉法。隐式欧拉法的单步计算代价较高，但是允许更大的时间步长，这反而提高了仿真的效率，并且极大地改善了系统的稳定性。二者对比的一个实例可参见图 21.6。

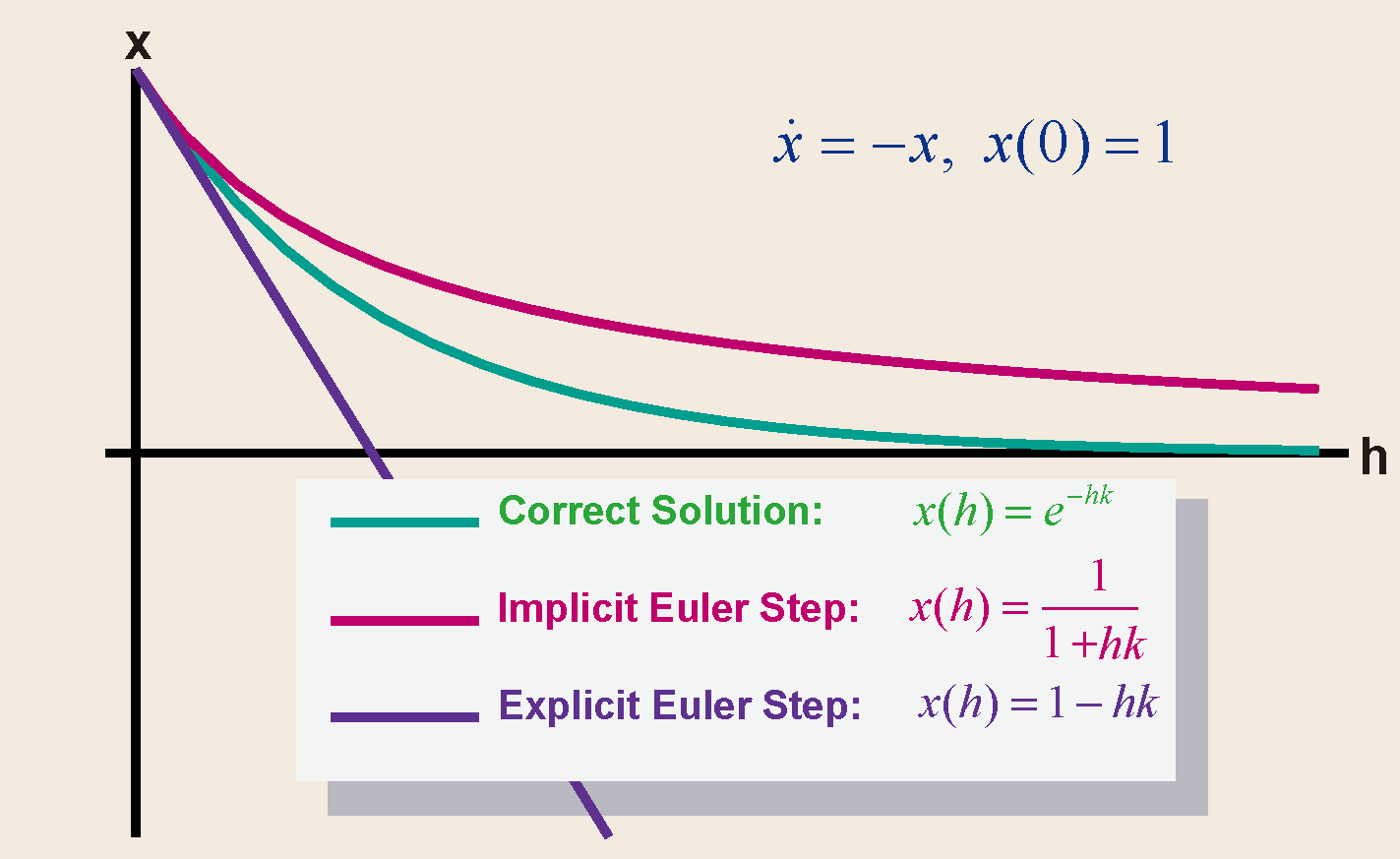
../../_images/animation-elastomers-euler.png — 图 21.6 显式欧拉积分与隐式欧拉积分的单步对比。对于微分方程 \(\dot{x}=-kx\)，考察分别按照显式欧拉法和隐式欧拉法递进时间步长为 \(h\) 的一步后与准确解之间的差距。以 \(x(0)=1\) 为初始状态，取系数 \(k=1\)，可作出图像。可以看到，当时间步长较大，显式欧拉法的误差将快速增长并因此容易导致仿真崩溃，而隐式欧拉法则允许更大的时间步长，因此具有较好的稳定性。[2]#

21.1.5. 数值求解#

接下来我们尝试对隐式欧拉积分中的方程组进行求解，设需要最小化的目标能量函数为 \(g(\boldsymbol x)=\frac{1}{2h^2}\|\boldsymbol x-\boldsymbol y^k\|^2_{\boldsymbol M}+E(\boldsymbol x)\)。一个经典方法是牛顿法，它是一个基于迭代的优化算法，其思想是每轮迭代都用二次函数逼近目标函数，并在该轮迭代中找到二次函数的最小值作为新的尝试解。迭代算法会依次求解出一个尝试序列 \(\{\boldsymbol x_{(i)}\}_{i=0}^{m-1}\)，其中 \(\boldsymbol x_{(i)}\) 表示第 \(i\) 轮迭代的尝试解（请注意，粒子 \(i\) 的位置表示为 \(\boldsymbol x_i\)，为了进行区分，我们把表示第 \(i\) 论迭代量的下标加了括号），每一轮迭代算法会从 \(\boldsymbol x_{(i)}\) 计算下一轮 \(\boldsymbol x_{(i+1)}\)，一般来讲序列 \(\{\boldsymbol x_{(i)}\}\) 会收敛到一个稳定解，最后我们把这个稳定解作为全局最小值点的近似（当然对于很复杂的优化问题，我们可能只能找到一个局部极小值点，甚至无法让算法收敛）。如何选取一个最好的二次函数呢？我们可以对目标函数在当前尝试解 \(\boldsymbol x_{(i)}\) 处进行二阶泰勒展开：

(21.11)#\[ g(\boldsymbol x)=g(\boldsymbol x_{(i)})+\nabla g(\boldsymbol x_{(i)})\cdot(\boldsymbol x-\boldsymbol x_{(i)})+\frac 12(\boldsymbol x-\boldsymbol x_{(i)})^\top\boldsymbol H_g(\boldsymbol x_{(i)})(\boldsymbol x-\boldsymbol x_{(i)})+O(\|\boldsymbol x-\boldsymbol x_{(i)}\|^3)。 \]

这里我们把梯度写成列向量 \(\nabla g(\boldsymbol x_{(i)})=\begin{bmatrix}\frac{\partial g(\boldsymbol x_{(i)})}{\partial x}\\\frac{\partial g(\boldsymbol x_{(i)})}{\partial y}\\\frac{\partial g(\boldsymbol x_{(i)})}{\partial z}\end{bmatrix}\)，\(\boldsymbol H_g(\boldsymbol x_{(i)})=\begin{bmatrix}\frac{\partial^2 g(\boldsymbol x_{(i)})}{\partial x^2}&\frac{\partial^2 g(\boldsymbol x_{(i)})}{\partial x\partial y}&\frac{\partial^2 g(\boldsymbol x_{(i)})}{\partial x\partial z}\\\frac{\partial^2 g(\boldsymbol x_{(i)})}{\partial x\partial y}&\frac{\partial^2 g(\boldsymbol x_{(i)})}{\partial y^2}&\frac{\partial^2 g(\boldsymbol x_{(i)})}{\partial y\partial z}\\\frac{\partial^2 g(\boldsymbol x_{(i)})}{\partial x\partial z}&\frac{\partial^2 g(\boldsymbol x_{(i)})}{\partial y\partial z}&\frac{\partial^2 g(\boldsymbol x_{(i)})}{\partial z^2}\end{bmatrix}\) 是 \(g\) 的海瑟矩阵（Hessian matrix）。我们忽略三阶小量 \(O(\|\boldsymbol x-\boldsymbol x_{(i)}\|^3)\)，就得到了一个用于近似 \(g(\boldsymbol x)\) 的二次函数（请注意，这个近似仅仅是对 \(g(\boldsymbol x)\) 在 \(\boldsymbol x_{(i)}\) 附近的近似，当 \(\boldsymbol x\) 太远的时候三阶“小”量将不能忽略！），下一轮迭代的尝试解 \(\boldsymbol x_{(i+1)}\) 取这个二次函数的极小值，通过对式 (21.11) 两边求梯度，再代入 \(\boldsymbol x_{(i+1)}\) 可得

\[ \nabla g(\boldsymbol x_{(i+1)})\approx\nabla g(\boldsymbol x_{(i)})+\boldsymbol H_g(\boldsymbol x_{(i)})(\boldsymbol x_{(i+1)}-\boldsymbol x_{(i)})=\boldsymbol 0。 \]

依此求得下一轮的尝试解：

(21.12)#\[ \boldsymbol x_{(i+1)} = \boldsymbol x_{(i)} - \boldsymbol{H}_g^{-1}(\boldsymbol x_{(i)})\nabla g(\boldsymbol x_{(i)})。 \]

牛顿法相比于普通的梯度下降法（gradient descent）能做到更快的收敛。而它的缺点在于，每步迭代中需要求解 \(\boldsymbol{H}_g\) 矩阵的逆，计算代价较大，且一般要求 \(\boldsymbol{H}_g\) 为正定矩阵，否则方程可能无解（牛顿法一般用于解凸优化问题）或解不出正确下降方向。

在此基础上还有拟牛顿法（quasi-Newton method）、柏萝登-弗莱彻-戈德福布-生纳法（Broyden-Fletcher-Goldfarb-Shanno method，BFGS method）等。为了避免海瑟矩阵的计算和存储，共轭梯度法（conjugated gradient）也是常用的优化方法之一。更多的优化算法这里不再赘述。

对于本节中的弹簧质点系统，\(g(\boldsymbol x)\) 性质足够好，我们认为只需要进行一步牛顿迭代即可求得最小值点（这里是一个简化的假设，事实上 \(g(\boldsymbol x)\) 不是凸函数）。我们只需要将式 (21.12) 中的 \(\boldsymbol x_{(i)}\) 和 \(\boldsymbol x_{(i+1)}\) 分别替换成 \(\boldsymbol x^k\) 和 \(\boldsymbol x^{k+1}\) 即可。所以我们需要解如下关于 \(\boldsymbol x^{k+1}-\boldsymbol x^k\) 的方程组，随后即可计算出 \(\boldsymbol x^{k+1}\) 和 \(\boldsymbol v^{k+1}\)：

(21.13)#\[ \boldsymbol H_g(\boldsymbol x^k)(\boldsymbol x^{k+1}-\boldsymbol x^k)=-\nabla g(\boldsymbol x^k)。 \]

现在我们来计算 \(\nabla g(\boldsymbol x)\) 和 \(\boldsymbol H_g(\boldsymbol x)\)，由 \(g(\boldsymbol x)\) 的定义得

(21.14)#\[\begin{split} \nabla g(\boldsymbol x)&=\frac 1{h^2}\boldsymbol M(\boldsymbol x-\boldsymbol y^k)+\nabla E(\boldsymbol x)，\\ \boldsymbol H_g(\boldsymbol x)&=\frac 1{h^2}\boldsymbol M+\boldsymbol H(\boldsymbol x)， \end{split}\]

其中 \(\boldsymbol H(\boldsymbol x)\) 是弹性势能 \(E(\boldsymbol x)\) 的海瑟矩阵。我们在式 (21.3) 中已经写出了对于一根弹簧的能量 \(E_{ij}\) 关于一个质点 \(i\) 的梯度 \(\nabla_iE_{ij}(\boldsymbol x)\) 的表达式，那么总能量对质点 \(i\) 的梯度即为

\[ \nabla_iE(\boldsymbol x)=\sum_j\nabla_iE_{ij}(\boldsymbol x)。 \]

总能量关于所有质点位置的梯度就是将关于每个质点的梯度拼接起来（假设总共有\(n\)个质点）：

(21.15)#\[\begin{split} \nabla E(\boldsymbol x)=\begin{bmatrix}\nabla_1E(\boldsymbol x)\\\vdots\\\nabla_nE(\boldsymbol x)\end{bmatrix}。 \end{split}\]

同样地，我们考虑一个弹簧 \((i,j)\) 关于质点 \(i\) 的海瑟矩阵，即对式 (21.3) 两边求梯度，得到

\[\begin{split} \boldsymbol H_e\mathrel{\mathop:}=\frac{\partial^2E_{ij}(\boldsymbol x)}{\partial\boldsymbol x_i^2}&=k_{ij}\frac{(\boldsymbol x_i-\boldsymbol x_j)(\boldsymbol x_i-\boldsymbol x_j)^\top}{\|\boldsymbol x_i-\boldsymbol x_j\|^2}+k_{ij}\left(1-\frac{l_{ij}}{\|\boldsymbol x_i-\boldsymbol x_j\|}\right)\left(\mathbf I-\frac{(\boldsymbol x_i-\boldsymbol x_j)(\boldsymbol x_i-\boldsymbol x_j)^\top}{\|\boldsymbol x_i-\boldsymbol x_j\|^2}\right)，\\ \frac{\partial^2E_{ij}(\boldsymbol x)}{\partial\boldsymbol x_i\partial\boldsymbol x_j}&=-\boldsymbol H_e，\\ \frac{\partial^2E_{ij}(\boldsymbol x)}{\partial\boldsymbol x_j^2}&=\boldsymbol H_e。 \end{split}\]

那么这个弹簧关于所有质点坐标的海瑟矩阵可以写成如下形式：

\[\begin{split} \boldsymbol H_{ij}(\boldsymbol x)= \begin{bmatrix} &\vdots&&\vdots&\\ \cdots&\boldsymbol H_e&\cdots&-\boldsymbol H_e&\cdots\\ &\vdots&&\vdots&\\ \cdots&-\boldsymbol H_e&\cdots&\boldsymbol H_e&\cdots\\ &\vdots&&\vdots& \end{bmatrix}， \end{split}\]

将 \(\boldsymbol H_{ij}(\boldsymbol x)\) 划分成 \(n\times n\) 个 \(3\times 3\) 的块，则第 \(i\) 行第 \(i\) 列与第 \(j\) 行第 \(j\) 列的块为 \(\boldsymbol H_e\)，而第 \(i\) 行第 \(j\) 列与第 \(j\) 行第 \(i\) 列的块为 \(-\boldsymbol H_e\)，其余块均为零矩阵。总能量的海瑟矩阵即为所有弹簧海瑟矩阵之和：

(21.16)#\[ \boldsymbol H(\boldsymbol x)=\sum_{(i,j)}\boldsymbol H_{ij}(\boldsymbol x)。 \]

最后，我们将式 (21.15)、(21.16) 代入到式 (21.14) 中计算 \(\nabla g(\boldsymbol x^k)\) 和 \(\boldsymbol H_g(\boldsymbol x^k)\)，然后即可求解方程 (21.13)。