图像补全与融合

7.2. 图像补全与融合#

在图像补全（image completion） 任务中，我们需要对图像缺失的部分进行填充，并确保填充后的结果尽可能合理，如图 7.11 和图 7.12 所示。“合理”是指尽可能平滑，具体可描述为以下两点：

  • 空间局部性（spatial locality）：图像中同一个物体上相邻的部分应该相似。

  • 奥卡姆剃须刀原则（Occam’s razor）：被填补的区域不应该存在任何多余的东西，即无法从非填充区域推理得出的东西。

../../_images/inpainting-lake-before.png
../../_images/inpainting-lake-after.png

图 7.11 左图中湖中心缺失了一块，使用算法补全之后效果如右图#

../../_images/inpainting-old_man-before.png
../../_images/inpainting-old_man-after.png
../../_images/inpainting-old_man-original.png

图 7.12 图像补全一个更极端的例子，我们甚至可以从左图恢复出中间的图片，右边是原图像#

图像融合（image cloning） 是另一个问题，指的是我们将一张图片的一个物体扣下来，粘贴到另一张图片上，还要保证粘贴的结果尽可能自然，仿佛另一张图片中真的有这么一个物体，如图 7.13 和图 7.14 所示。

../../_images/cloning-log.png

图 7.13 无缝图像融合的一个例子。使用泊松图像编辑完成这个任务只需要原图 (最左侧) 中大致圈出树干的区域即可。直接将截取的部分贴到目标图像中，并进行简单的颜色调整，得到的图片会有明显的作图痕迹 (倒数第二列)；使用泊松图像编辑可以让这截树干看上去就像真的摆放在相应的场景中 (最右一列)。#

../../_images/cloning-math.png

图 7.14 无缝图像融合的另一个例子。左侧是原图和背景图，中间是将原图进行精细抠图之后直接贴到背景图上的效果，右侧是使用泊松图像编辑加上梯度混合处理后的效果。#

这两个问题都可以使用泊松编辑（Poisson editing） 来解决。接下来，我们会形式化地描述要解决的问题，然后介绍泊松图像编辑技术具体是如何解决的，最后再介绍一些泊松图像编辑的拓展应用。

7.2.1. 问题描述#

在数学上，我们可以用梯度的大小来衡量图片的变化程度，所以平滑的意思就是让图片亮度的梯度尽可能小。如图 7.11 所示，我们设 \(\Omega\) 表示待填补区域所有像素点的集合，\(\partial\Omega\) 为与待填补区域相邻的所有已知像素点的集合，\(f(x,y)\) 为定义在 \(\Omega\cup\partial\Omega\) 上的颜色场，表示要填补的内容，\(f^*(x,y)\) 为定义在 \(\Omega\) 的补集上的颜色场，表示图片的已知部分。那么我们可以将图像补全任务表达为如下最优化问题：

(7.11)#\[ \min_f\iint_\Omega\|\nabla f\|^2\mathrm dx\mathrm dy,\quad\text{s.t.}\quad f|_{\partial\Omega}=f^*|_{\partial\Omega} \]

含义就是找到一个颜色场 \(f\) 使得内部的梯度尽可能小，同时边界上能够无缝衔接。

图像补全的任务只能为图像填上一部分“空白”，就像图 7.11 中被填补的湖水一样。如果我们希望填补上用户指定的内容，这个问题就变成了无缝图像融合任务。在图像融合任务中，我们还额外需要一个源图像 (比如图 7.13 中截取出来的木头)，源图像的形状、大小与待填补区域完全一致。

与图像补全任务不同的是，我们需要在图像融合的过程中保留源图像的纹理信息，也就是要尽可能地保留源图像的梯度。记源图像为定义在 \(\Omega\) 上的颜色场 \(g(x,y)\)，那么图像融合任务可以表达为如下最优化问题：

(7.12)#\[ \min_f\iint_\Omega\|\nabla f-\nabla g\|^2\mathrm dx\mathrm dy,\quad\text{s.t.}\quad f|_{\partial\Omega}=f^*|_{\partial\Omega} \]

含义就是我们需要让填补部分 \(f\) 的梯度与 \(g\) 的梯度尽可能接近，同时保证边界上无缝衔接。

7.2.2. 求解#

由于公式 (7.11) 是公式 (7.12) 的特殊情况 (\(g\) 取常值函数)，我们只需要考虑如何求解公式 (7.12)。这是对一个连续函数的最小化问题，也就是泛函优化问题，需要借助欧拉-拉格朗日方程[1]。这里我们直接给出结论，公式 (7.12) 中优化目标取极值当且仅当 \(f\) 满足如下狄利克雷边界条件的泊松方程：

(7.13)#\[ \nabla^2f=\nabla^2g,\quad\text{s.t.}\quad f|_{\partial\Omega}=f^*|_{\partial\Omega} \]

其中 \(\nabla^2=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\) 为拉普拉斯算子。这也是泊松图像编辑名字的由来。我们需要求解的是颜色场 \(f\)，在离散场景下，我们需要求的是 \(\Omega\) 中每个像素点上 \(f(x,y)\) 的值。我们可以使用上一节公式 (7.10) 中介绍的离散 Laplacian 算子代入公式 (7.13) 中，右手项可以直接计算出结果，左手项展开为：

(7.14)#\[ \nabla^2f(x,y)=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y) \]

对于大多数 \(\Omega\) 内的像素点，公式 (7.14) 中的五个 \(f\) 值都是待求的未知数。但是对于在边界上的像素点 (和 \(\partial\Omega\) 相邻的像素点)，其四个相邻的像素点不全在 \(\Omega\) 中，此时我们就需要借助公式 (7.13) 中的边界条件，把公式 (7.14) 中相应的邻居项换成 \(f^*\) 的取值。举个例子，如图 7.15 所示，计算 \((2,2)\) 处的拉普拉斯时，其左、上邻居为 \(\partial\Omega\) 内的像素点，所以这两项需要替换成 \(f^*\) 的值，即：

(7.15)#\[ \nabla^2f(2,2)=f(3,2)+f^*(1,2)+f(2,3)+f^*(2,1)-4f(2,2) \]
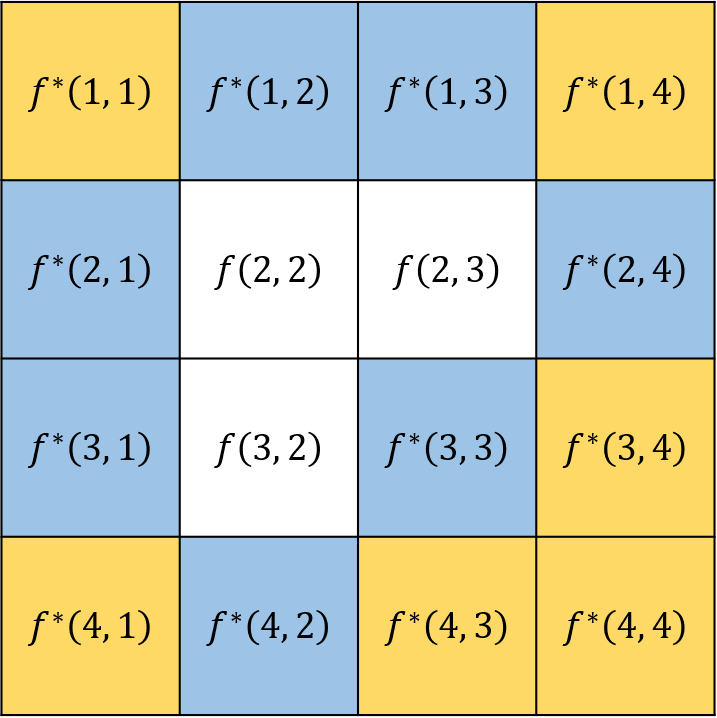
../../_images/poisson_editing-boundary.png

图 7.15 待填补的像素示例。其中白色为 \(\Omega\)，蓝色为 \(\partial\Omega\)，橙色为剩余的图片已知部分。#

于是这个像素的 \(\nabla^2f\) 中只包含了三个未知数。对于每个 \(\Omega\) 中的像素 \((x,y)\)，我们都可以写出一个方程 \(\nabla^2f(x,y)=\nabla^2g(x,y)\)；对于这个方程，要将修改为 \(f^*\) 的项移到等号右边，保证等号左边只包含未知量的一次项，常数项均移到等号右边。例如，图 7.15 中像素 \((2,2)\) 处的方程应当写为：

(7.16)#\[ f(3,2)+f(2,3)-4f(2,2)=\nabla^2g(2,2)-f^*(1,2)-f^*(2,1) \]

这样，我们就得到了一个含有 \(|\Omega|\) 个方程、关于 \(f(x,y),\forall(x,y)\in\Omega\) 的线性方程组。方程与未知数个数相等，求解线性方程组可以得到唯一解。

我们可以进一步将所有的 \(f(x,y)\) 排成一个向量 \(\mathbf f\)，并将这个线性方程组写成 \(\mathbf L\mathbf f=\mathbf b\) 的形式。对于图 7.15 所示的例子，矩阵 \(\mathbf L\) 为：

(7.17)#\[\begin{split} \mathbf L=\begin{bmatrix} -4 & 1 & 1 \\ 1 & -4 & 0 \\ 1 & 0 & -4 \end{bmatrix} \end{split}\]

向量 \(\mathbf b\) 为：

(7.18)#\[\begin{split} \mathbf b=\begin{bmatrix} \nabla^2g(2,2)-f^*(1,2)-f^*(2,1) \\ \nabla^2g(2,3)-f^*(1,3)-f^*(2,4)-f^*(3,3) \\ \nabla^2g(3,2)-f^*(3,1)-f^*(3,3)-f^*(4,2) \end{bmatrix} \end{split}\]

未知量按如下顺序排成向量 \(\mathbf f\)：

(7.19)#\[\begin{split} \mathbf f=\begin{bmatrix} f(2,2) \\ f(2,3) \\ f(3,2) \end{bmatrix} \end{split}\]

在这个问题中，我们可以分析 \(\mathbf{L}\) 所具有的一些性质：

  • 稀疏性：由于每行只与至多 5 个未知数相关，\(\mathbf L\) 是一个稀疏矩阵。

  • 对称性：在 \(\Omega\) 内，如果 \((x_1,y_1)\) 与 \((x_2,y_2)\) 相邻，则 \(\nabla^2f(x_1,y_1)\) 中 \(f(x_2,y_2)\) 一项的系数为 \(1\)，且 \(\nabla^2f(x_2,y_2)\) 中 \(f(x_1,y_1)\) 一项的系数也为 \(1\)，否则都为 \(0\)，所以这两个系数永远相等。

  • 主对角占优：\(\mathbf L\) 的对角项为 \(-4\)，每一行除对角项外至多还有 4 个 1 (因为至多 4 个未知的邻居)，非对角项绝对值加起来不超过对角项绝对值。

对于这样的线性系统，有许多高效的求解器，这里列举三类，读者可以自行了解更多细节：

  • 直接求解法。如 LU 分解。

  • 迭代法。如雅克比 (Jacobi) 迭代、高斯-赛德尔 (Gauss-Seidel) 迭代、逐次超松弛 (SOR) 迭代。

  • 多重网格法。

7.2.3. 拓展应用#

接下来我们介绍一些无缝图像融合算法的拓展应用。

在上述算法的基础上，还可以根据任务的需要加一些简单的处理，达到更加自然的效果。这些处理都是简单地将公式 (7.12) 中的 \(\nabla g\) 改成另外一个向量场 \(\mathbf v\)，从而求解的问题将变成下式：

(7.20)#\[ \min_f\iint_\Omega\|\nabla f-\mathbf v\|^2\mathrm dx\mathrm dy,\quad\text{s.t.}\quad f|_{\partial\Omega}=f^*|_{\partial\Omega} \]

对应的泊松方程变为：

(7.21)#\[ \nabla^2f=\nabla\cdot\mathbf v,\quad\text{s.t.}\quad f|_{\partial\Omega}=f^*|_{\partial\Omega} \]

所以再计算右手项的时候还需要一个离散的散度算子 \(\nabla \cdot \)。我们已经在上一节中介绍过 Sobel 算子，根据散度的定义，我们可以对向量场的每个分量使用相应的 Sobel 算子然后再相加。具体的公式留给读者推导。

7.2.3.1. 梯度混合#

对于图 7.14 所示的例子，如果简单地套用无缝图像融合算法，得到的效果会像图 7.16 一样过于平滑，没办法保留墙壁上凹凸不平的纹理。为解决这个问题，我们可以令

(7.22)#\[\begin{split} \mathbf v(x,y)= \begin{cases} \nabla f^*(x,y)&\|\nabla f^*(x,y)\|>\|\nabla g(x,y)\|\\ \nabla g(x,y)&\text{otherwise} \end{cases} \quad\forall(x,y)\in\Omega \end{split}\]

其中 \(f^*(x,y)\) 指的是背景图的颜色场。也就是说，我们要求 \(f\) 的梯度尽可能接近源图像和背景图梯度的较大值，这样就可以避免过度平滑的问题了。

../../_images/cloning-math-naive.png

图 7.16 不加梯度混合的效果#

7.2.3.2. 纹理抹平与去除#

有时我们希望将图像的一些纹理抹平，如图 7.17 所示，将孩子的脸变得更加光滑。将 \(\mathbf v\) 设为 \(\nabla g\)，并把其中梯度模长在一个阈值以下的部分修改为 \(\mathbf 0\)，即可得到这个效果。

../../_images/cloning-texture_remove.png

图 7.17 纹理抹平的效果#

我们还可以将图片的一些内容去除掉，如图 7.18 所示，我们可以在图片中选取一小片席子，用它的纹理替换掉梨的枝干。

../../_images/cloning-texture_replace.png

图 7.18 用席子的纹理替换掉梨的枝干#