6.4. 曲线光栅化#
曲线光栅化的基本思想和我们之前介绍的直线、多边形的光栅化基本一致,下面我们介绍几个常用的方法。
6.4.1. 细分#
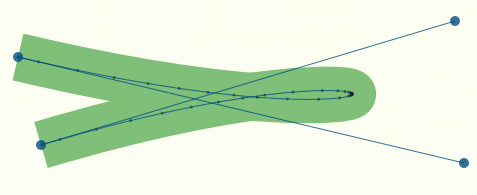
为了将曲线显示在屏幕上,我们同样需要对曲线进行光栅化操作将其转化成位点阵图。一个简单的想法是通过细分将曲线划分成若干段子曲线,每段子曲线的曲率小到足以用直线来近似,而后用绘制直线的方法来近似每段子曲线,不过这种做法需要在光滑度和计算复杂性之间寻求一个平衡。自适应细分(adaptive subdivision) 根据曲线不同位置的曲率大小动态地调整细分的程度,从而在弯曲程度较大的地方获得更多的细节而在平滑的地方节省算力,如图 6.19 所示。
6.4.2. 采样#
另一种想法则是采用曲线版本的 DDA 算法,即,根据参数 \(t\) 对曲线进行采样,并将采样对应的像素点绘制在屏幕上。为了提高效率,采样可以通过增量累加的方式进行的。
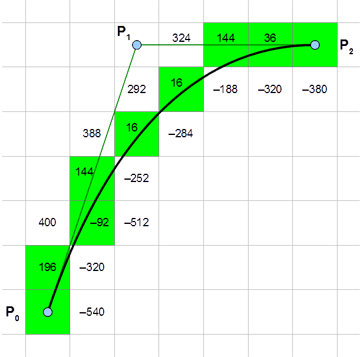
图 6.20 二阶贝塞尔曲线的光栅化#
与直线类似,我们也可以采用变体的布雷森汉姆算法。在曲线的情形下,像素点 \((x,\,y)\) 到曲线的偏差可以定义为 \(e=F(x,\,y)\),这里 \(F(x,\,y)\)是曲线转化成对应的隐式方程,当像素点在曲线上时,偏差值为0。因此曲线版本的布雷森汉姆算法可以如下设计[2]:对于曲线\(F(x,\,y)=0\),首先对曲线进行细分从而保证其分段单调。这里不妨假设其单增。当我们已绘制像素点 \((x,\,y)\),算法需要从 \((x+1,\,y),\,(x,\,y+1),\,(x+1,\,y+1)\) 中选取下一个需要绘制的点。算法以 \((x+1,\,y+1)\) 的角度考察是否需要在 \(x\) 或 \(y\) 方向上步进一个像素:分别计算偏差值 \(e_{x}=F(x,\,y+1),\,e_{y}=F(x+1,\,y),\,e_{xy}=F(x+1,\,y+1)\) 若偏差 \(\mathop{|}e_{xy}\mathop{|}<\mathop{|}e_x\mathop{|}\),则需要在 \(x\) 方向上加1;若偏差 \(\mathop{|}e_{xy}\mathop{|}<\mathop{|}e_y\mathop{|}\),则需要在 \(y\) 方向上加1。而这里由于曲线单增的假设,\(e_y\le e_{xy}\le e_x\)必然成立,故可以不计算绝对值,上述两个判断条件等价于:\(e_y+e_{xy}>0\) 及 \(e_{xy}+e_x<0\),由此来确定变体布雷森汉姆算法的下一个绘制点。一个实例如图 6.20 所示。
6.4.3. 扫描线#
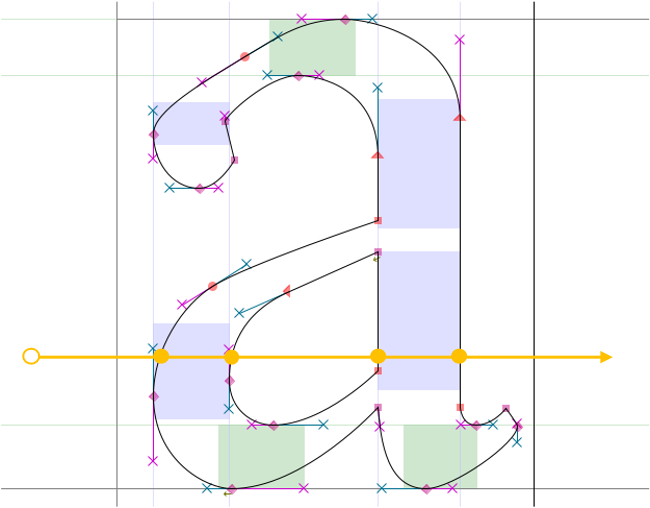
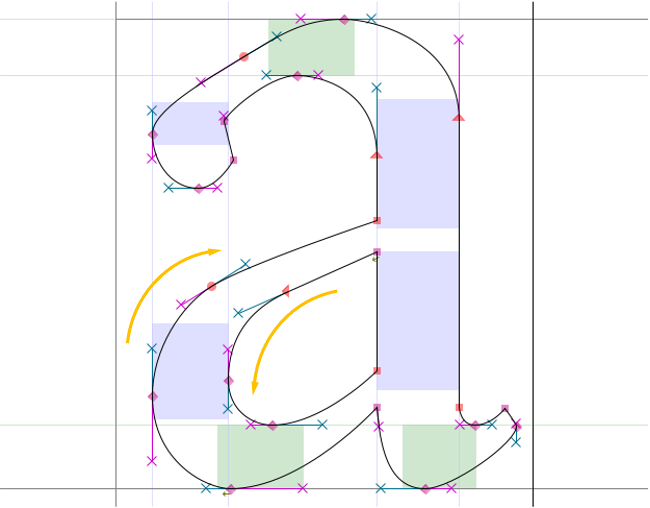
对于由曲线组成的图案,如图 6.21 中的字体,类似地可以利用扫描线方法绘制。当扫描线与图形产生多个交点时,第奇数交点到第偶数交点的中间线段对应需要绘制的像素,而第偶数交点到第奇数交点间的线段则不需要绘制(对应外部或图形的中间空洞)。TTF(truetype font)文件格式在渲染字体时将采用了类似的思想:将外部轮廓定义为顺时针环绕而内部轮廓定义为逆时针环绕,从某一像素点 \(P\) 向任意方向做射线,当自左向右跨越轮廓边界时将环绕数加1,自右向左跨越时将环绕数减1,于是当最终结果非零时则表示点 \(P\) 在内部,为零则表示在外部。 求解曲线与扫描线的交点需要求解一元方程,若曲线阶数大于三,则需要借助于牛顿下降法等数值工具进行求解。也因此图形学中更多应用低阶曲线,例如 TTF 字体由线段和二阶贝塞尔曲线组成。
另外,现代图形学中也为更高质量的曲线渲染引入了反走样算法、亚像素算法等改进方案,如图 6.22,这里不再展开。
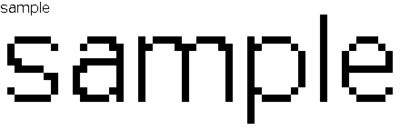
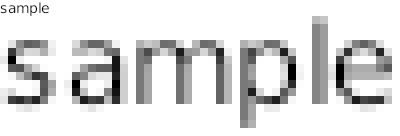
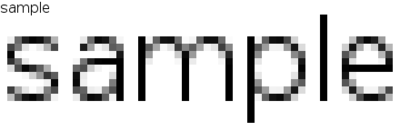
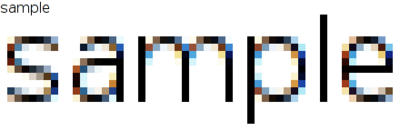
图 6.22 左上:简单光栅化;右上:无提示的抗锯齿光栅化;左下:带反锯齿与提示的光栅化;右下:RGB 平板显示器上的带提示和亚像素渲染的光栅化。[4]#