22.2. 碰撞与摩擦#
我们对刚体场景中最感兴趣的动态当属它们之间的碰撞了,只有多个物体相互接触并产生影响,才能够产生出复杂的动态。然而,物理仿真中的碰撞与摩擦是十分复杂的现象,学术和工业界也有许多十分精巧的处理方式,本节我们只介绍一种最简单但也有效的方法。无论方法如何,在处理碰撞与摩擦时,总是需要先检测碰撞是否发生,若发生再对其进行处理。
22.2.1. 碰撞检测#
碰撞检测的目的是判断当前时刻的状态下是否有碰撞发生,如果有,还需计算出碰撞发生的位置以便后续进行碰撞处理。为了简化问题,我们假设只检测一个质点是否与场景中的其他物体发生碰撞,且场景内其他物体互不相交。
对于“是否发生碰撞”这个问题,我们只需要检查质点是否在某一个物体“内部”即可;既然涉及到内部与外部的区分,读者不难联想到所有几何表达方式中 §9.3.1 提到的有符号距离场。我们将其他每个物体的边界都转换成有符号距离场,分别记为 \(\phi_1,\cdots,\phi_M\),设质点的位置坐标为 \(\boldsymbol x\),那么质点发生了碰撞当且仅当 \(\exists i,\phi_i(\boldsymbol x)\le 0\)。
对于“发生碰撞的位置在哪”这个问题,由于场景内其他物体没有相交,所以碰撞发生时必然只存在一个 \(i\) 满足 \(\phi_i(\boldsymbol x)\le 0\)。借助有符号距离场的性质,我们可以知道距离 \(\boldsymbol x\) 最近的表面位置是 \(\boldsymbol x^*=\boldsymbol x-\phi_i(\boldsymbol x)\nabla\phi_i(\boldsymbol x)\),这就是发生碰撞的位置。当然,想要算准 \(\boldsymbol x^*\),我们需要假设质点的位置离表面足够近,这在碰撞检测问题中是一个合理的假设,因为只要你正确处理了碰撞,一般情况下不会出现严重的穿模现象。另外,我们还可以计算出 \(\boldsymbol x^*\) 处的表面法向 \(\boldsymbol N=\nabla\phi_i(\boldsymbol x^*)\)。
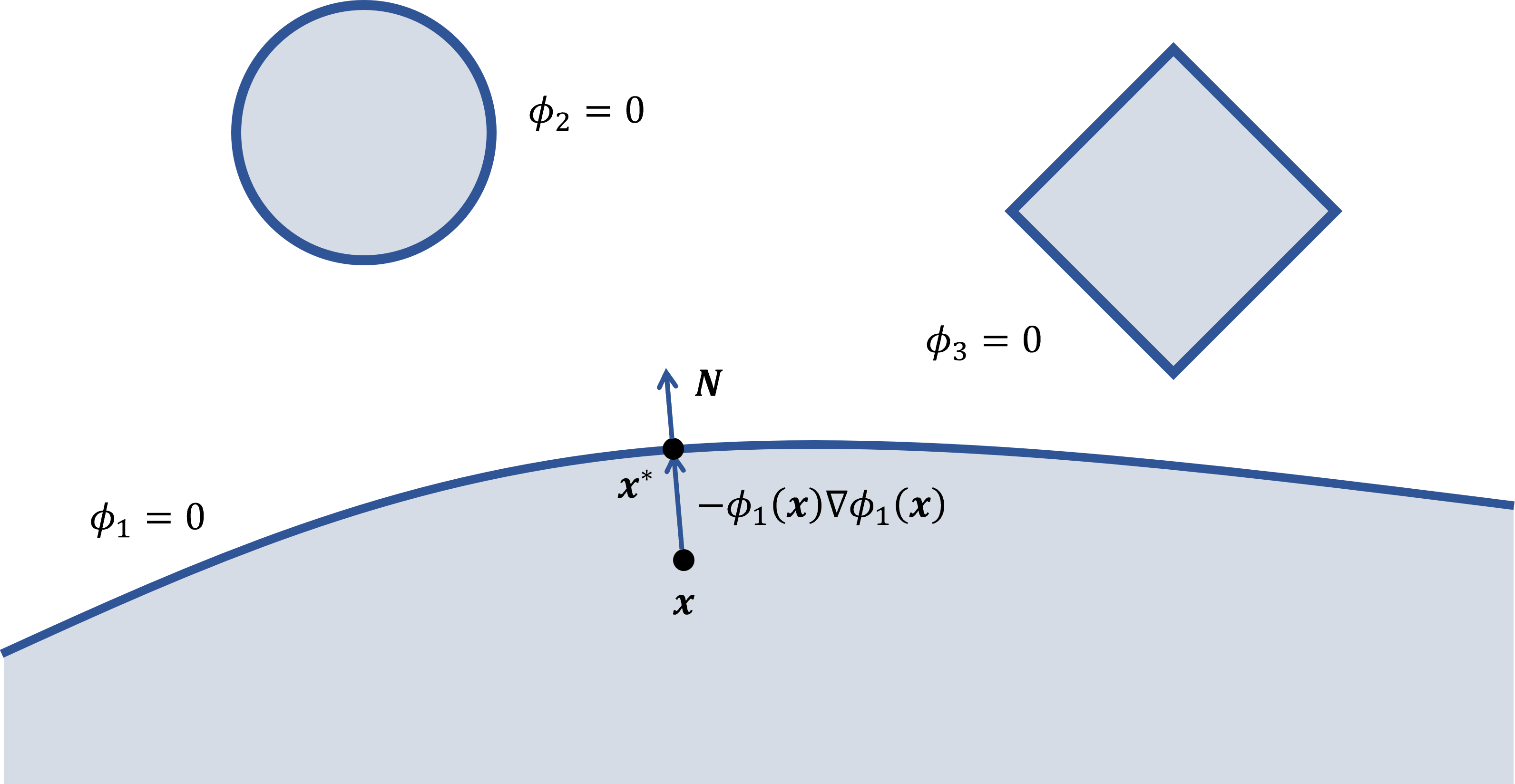
图 22.4 用有符号距离场表示场景中的物体,检测位于 \(\boldsymbol x\) 的质点是否发生碰撞,并找出碰撞点以及表面法向。#
对于更一般的情况,我们需要检测一个具有复杂形状的刚体是否发生了碰撞。由于这样的刚体通常会被表示成四面体网格,或者会用一个三角网格表示其表面,我们可以在刚体的表面进行采样,并对每个采样点进行碰撞检测。这个采样的过程可以在预处理阶段完成,计算好参考构型下的位置,在模拟过程中通过刚体的质心位置以及旋转即可算出采样点在当前时刻的位置。
如果场景中还有多个可动的刚体,还需要检测它们之间的碰撞。我们可以依次对每个刚体进行碰撞检测,记当前待检测的刚体编号为 \(i\),在其表面采样后,使用场景中剩余物体(包括场景中的静态边界以及除 \(i\) 之外的可动刚体)表面的有符号距离场检测每个采样点是否发生了碰撞。对于可动刚体 \(j\)(\(j\ne i\)),我们同样要在预处理阶段计算出其参考构型下的有符号距离场 \(\phi^\mathrm{ref}_j\),设当前时刻刚体 \(j\) 的质心位置是 \(\boldsymbol c_j\),旋转矩阵是 \(\boldsymbol R_j\),那么当前时刻它的有符号距离场就是 \(\phi_j(\boldsymbol x)=\phi^\mathrm{ref}_j\left(\boldsymbol R_j^\top(\boldsymbol x-\boldsymbol c_j)\right)\)。
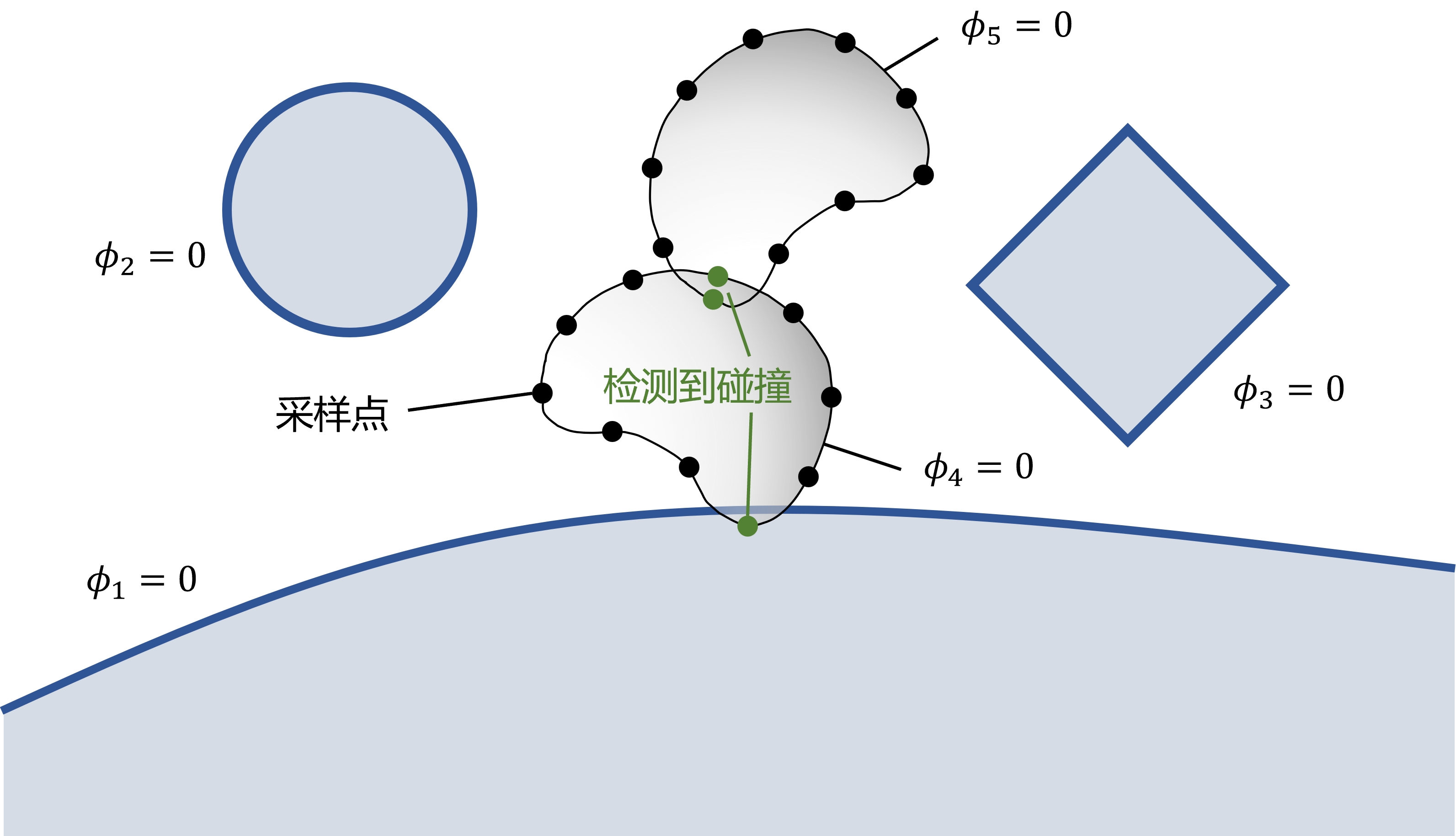
图 22.5 含有多个复杂形状可动刚体的碰撞检测#
22.2.2. 碰撞处理#
碰撞处理的目的是针对已经检测到的碰撞事件给出响应,更新相关物体的状态,以阻止穿模的发生。我们还是先将问题简化成场景中只有一个能动的质点,其余均为静态边界。本节我们给出一个最朴素的碰撞处理方式——惩罚方法(penalty method),通过施加力的方式模拟碰撞产生的效果,这个力分为两部分——惩罚力 \(\boldsymbol f_\mathrm{penalty}\) 和摩擦力 \(\boldsymbol f_\mathrm{friction}\)。
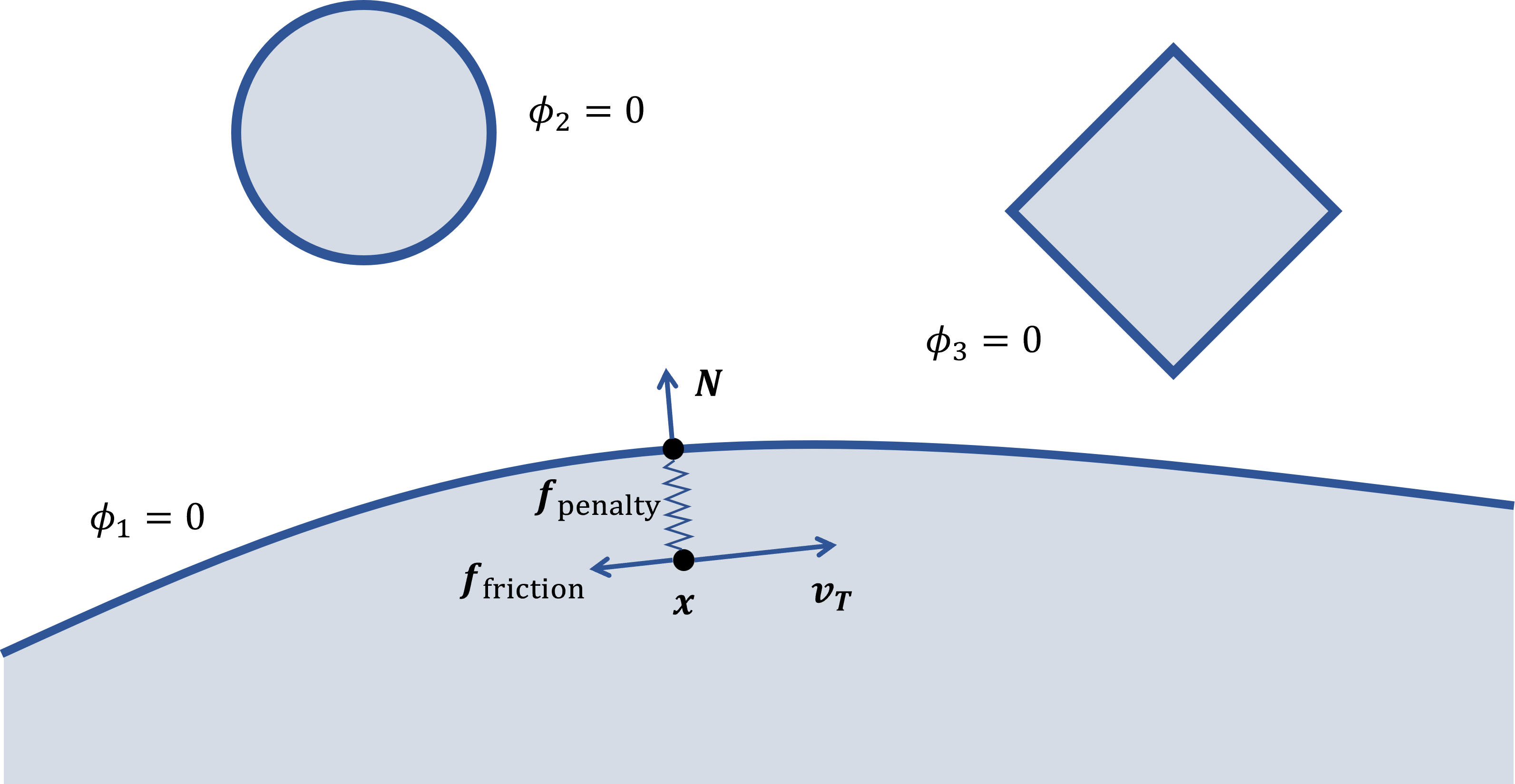
图 22.6 粒子与静态边界的碰撞响应#
惩罚力本质上是对粒子施加的一个弹力:
这个力的表现等价于添加了一根两端分别在 \(\boldsymbol x^*\) 和 \(\boldsymbol x\) 的、原长为 \(0\) 的弹簧,可以起到将粒子推出边界的效果。
摩擦力是一个与质点沿表面的切向速度相反的力,它会阻碍质点与障碍物之间的相对滑动。我们这里采用库伦模型(Coulomb friciton)来计算,即存在相对滑动时,摩擦力的大小与正压力(即我们这里的 \(\boldsymbol f_\mathrm{penalty}\))成正比,此时称为动摩擦(dynamic friction);不存在相对滑动时,摩擦力会恰好抵消相对滑动趋势,此时称为静摩擦(static friction)。设质点的速度为 \(\boldsymbol v\),则其相对边界的切向速度可由法向计算得到:
那么摩擦力可以表示为与速度相反的一个向量:
其中 \(a\ge 0\) 是一个待定系数,我们将通过库仑模型计算出它的大小。若此时处于静摩擦的状态,则 \(\boldsymbol f_\mathrm{friction}\) 的作用会刚好抵消掉相对滑动趋势,换句话说,在时间步长 \(h\) 内 \(\boldsymbol f_\mathrm{friction}\) 产生的冲量恰好与当前时刻切向方向的动量相反:
其中 \(m\) 为质点的质量,求解此方程得到 \(a=\frac mh\)。若此时处于动摩擦的状态,则 \(\boldsymbol f_\mathrm{friction}\) 的大小恰好等于 \(\boldsymbol f_\mathrm{penalty}\) 大小的常数倍,这个常数又被称为摩擦系数,记为 \(\mu\),我们以此列出另一个方程:
求解得到 \(a=\mu k\frac{\vert\phi_i(\boldsymbol x)\vert}{\Vert\boldsymbol v_\boldsymbol T\Vert}\)。现在的问题是:如何判断处于静摩擦还是动摩擦的状态呢?当阻止相对滑动趋势所需要的力的大小超过了滑动摩擦所能够提供的力的大小,则毫无疑问会产生相对滑动,此时适用动摩擦的情形;反之,摩擦力足以抗拒相对滑动,质点与障碍物应保持相对静止,此时适用静摩擦的情形。所以最终 \(a\) 的值应当取上述两个方程解的较小值:
因此,碰撞处理最终的结果就是为质点添加了外力 \(\boldsymbol f_\mathrm{penalty}+\boldsymbol f_\mathrm{friction}\),如图 22.6 所示。
到这里读者不难发现,这个方法有个很大的缺陷,即只有在粒子一定程度地陷入障碍物之后,碰撞响应才能够生效,这就导致我们无法避免穿模现象的发生。一个简单的处理方式是将所有物体的边界向外扩张 \(\varepsilon\),方法是将碰撞检测和碰撞处理中涉及到的有符号距离场 \(\phi_i(\boldsymbol x)\) 替换为扩张后的有符号距离场 \(\hat\phi_i(\boldsymbol x)=\phi_i(\boldsymbol x)-\varepsilon\),如图所示。这会导致在粒子距离某个边界小于 \(\varepsilon\) 时,碰撞响应就会生效,从而减少粒子穿模的情况。
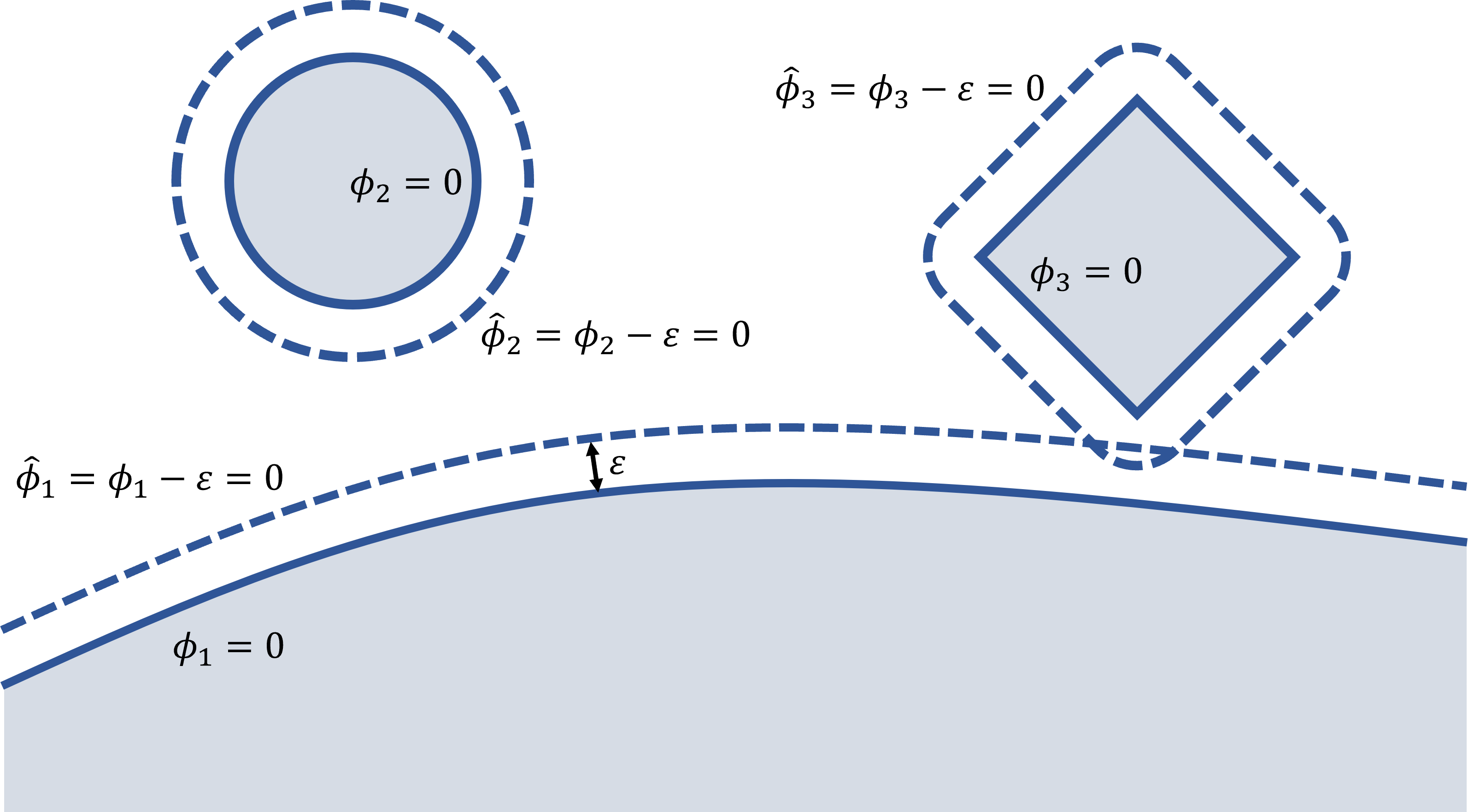
图 22.7 为碰撞检测和处理增加缓冲区域。图中实线为原边界,虚线为原边界向外扩张 \(\varepsilon\) 后的边界。#
惩罚方法最大的好处之一是可以直接拓展到一般形状刚体的情形,我们对每个发生碰撞的采样点求出碰撞响应后施加的力,将这些力当作外力直接作用到响应的采样点上即可。因此我们只需要用碰撞响应后的结果更新 §22.1.3 第 1 步中的外力 \(\boldsymbol F\) 和外力矩 \(\boldsymbol\tau\) 即可。需要额外注意的一点是,在计算两个可运动刚体之间的碰撞产生的摩擦力时,式 (22.7) 中的 \(\boldsymbol v\) 要替换成当前采样点相对于另一个刚体表面的碰撞点的速度。
22.2.3. 其他碰撞检测和处理的方法#
我们在 §22.2.1 中介绍了通过采样的方式对连续介质进行碰撞检测,这是一种最简单的办法,它的缺点也很明显——采样点过多会导致碰撞检测次数变多,从而降低计算效率;采样点过少则会导致算法遗漏更多的碰撞事件,从而引起较为严重的穿模现象。事实上,对于四面体或三角网格表示的刚体形状,还可以基于判断三角面片是否相交的算法实现更加精确的碰撞检测 [WFS+21],有些研究工作甚至针对高阶曲面的几何表达方式设计了碰撞检测算法 [FJZ+23];更高级的碰撞检测方法还会把这个问题看成与时间和速度相关的问题,这类方法并不在物体已经发生微量穿模的时候检测碰撞,而是在碰撞前通过物体的速度预测一个未来最早发生碰撞的时间 [FLS+21]……物理模拟中的碰撞检测是一个很困难的开放性问题,学术界对此有大量的研究工作,若读者不满足于仅仅模拟出一个简单的刚体场景,可以查阅相关的文献以深入学习。
在 §22.2.2 中介绍的惩罚方法看上去很完美——它能够解决各种复杂的情况,同时还能完美地结合到刚体仿真的时间积分算法中。但是如果实现一边就会发现其中会有很多难以把握的细节,例如为了防止模拟过程中出现相距一定距离的物体之间仍然表现出斥力的现象,我们会希望 \(\varepsilon\) 尽可能小,与此同时增加 \(k\) 以让惩罚力足够大来防止穿模;但由于我们采用的是显式时间积分,这样会导致模拟变得十分不稳定,具体原因可以参考 §21.1.4.1。
可以看出,碰撞处理也是一个十分困难的问题,它也是学术界一个热门的方向之一。但这不意味着惩罚方法的效果很差,目前碰撞效果最逼真的方法就是用惩罚方法做的 [LFS+20],它把式 (22.6) 中惩罚力的形式换成了 \(\boldsymbol f_\mathrm{penalty}=\rho\frac 1{\phi_i(\boldsymbol x)}\boldsymbol N\),因此在系统中引入了一项对数形式的增量势能(incremental potential,IP),因此这个方法也被称为增量势能碰撞(incremental potential,IPC);注意到这个修改后的惩罚力是在障碍物外是一个将物体向外推的斥力,一旦越过障碍物的边界,就会变成将物体向内吸,因此在这个方法中需要采取更加高级的碰撞检测算法,通过修改时间步长来避免穿模的发生,在穿模发生前就将碰撞处理好,并且还采用了隐式时间积分。
还有另外一类碰撞处理的方法叫做冲量法(impulse method),这类方法不再通过加力的方式处理碰撞,而是直接修改速度,也即在当前时间步内给物体施加一个冲量 [Bar01]。这个方法会比惩罚方法复杂,尤其是涉及到多个刚体同时发生碰撞时,冲量法需要求解一个较大的线性系统以获得速度更新。