三维几何变换

12.2. 三维几何变换#

三维空间的几何变换，在二维的基础上增加了 \(z\) 轴，三维空间中的旋转和缩放很容易从二维扩展过来，

(12.10)#\[\begin{split} \begin{aligned} \mathbf{D} = \begin{bmatrix} 1 & 0 & 0 & d_x \\ 0 & 1 & 0 & d_y \\ 0 & 0 & 1 & d_z \\ 0 & 0 & 0 & 1 \end{bmatrix},\, \mathbf{P} = \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}. \end{aligned} \end{split}\]

但是，三维旋转却要复杂不少。因为二维空间上的旋转，仅仅是围绕垂直于 \(xy\) 平面的轴旋转，而三维空间的旋转可以围绕任意一根轴进行旋转。本节只介绍两种最基础的旋转表示方法，欧拉角和旋转向量，并简要分析它们的优缺点。

12.2.1. 旋转的欧拉角表示#

../../_images/euler.png

图 12.3 航空领域中的欧拉角，表示为偏航角（yaw），俯仰角（pitch），翻滚角（roll）[1]。#

欧拉角是用来描述三维空间中刚体的转动角度的三个独立角度，最早由欧拉于1776年提出来，所以也被称为欧拉角。

三维旋转包含三个自由度，欧拉角将三个自由度分别给了三个确定的轴，即用绕三个确定轴的旋转来表示任意旋转。欧拉角的表示方法很多，以常见的航空领域的用法为例。

  1. 先绕全局的 \(Z\) 轴旋转（偏航角），这时候目标自己的坐标系也发生了旋转；

  2. 再绕自己的 \(Y\) 轴旋转（俯仰角）；

  3. 最后绕自己的 \(X\) 轴旋转（滚转角）。

这里的旋转顺序是 \(ZYX\)，实际上，欧拉角的选取有很多种，除了用三个不同的轴，也有用两个轴（如 \(ZXZ\)）的表示方法，以及绕固定轴（全局）和运动轴（局部）的区别。这里有一个很有意思但不直观的结论，留给读者证明：三次绕固定轴旋转的最终姿态和以相反顺序三次绕运动轴旋转的最终姿态相同。

提示

欧拉角有一个很常见的问题——万向锁（gimbal lock）。万向锁是指在动态表示（\(ZYX\)）下，当俯仰角等于 \(\pm 90\) 度时，第三次旋转和第一次旋转效果等价，丢失了一个表示维度的问题。直观上理解，当俯仰角等于 \(\pm 90\) 度时，局部坐标系下的 \(X\) 轴，被旋转到了全局坐标系下的 \(Z\) 轴上，与最开始绕 \(Z\) 轴旋转也就具有相同的旋转效果。对于欧拉角来说，万向锁是无法避免的问题，为了尽可能减少万向锁的影响，不同的专业领域会选择不同的旋转轴和转序。

12.2.2. 旋转的轴角表示#

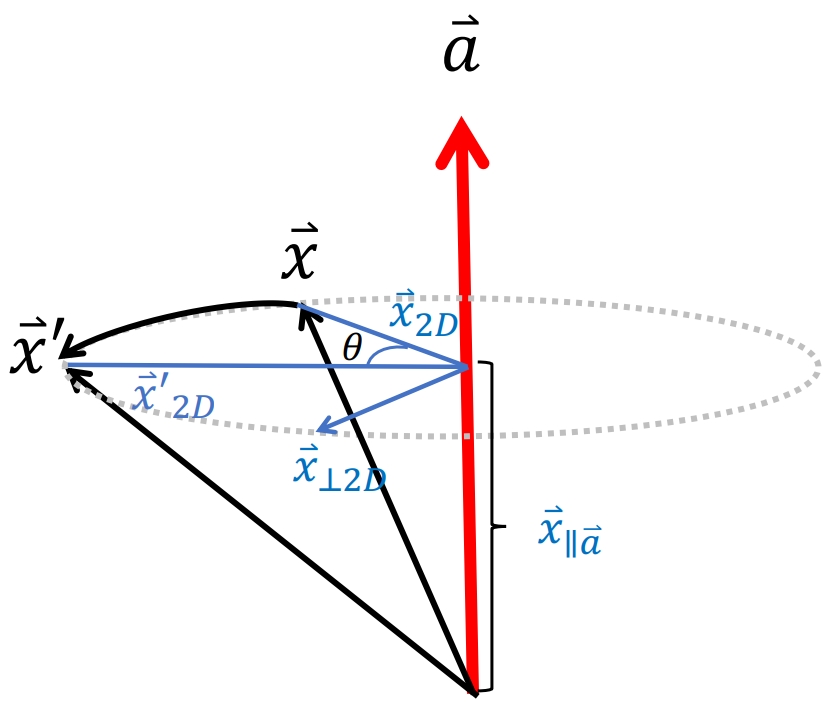
../../_images/axis-angle.png

图 12.4 轴角表示法。#

欧拉角虽然很常用，但它依赖于坐标轴的选定，且存在万向锁的问题。轴角表示法是更普遍的旋转表示：假设有一根经过原点的旋转轴 \(\vec{a}\)（如果不经过原点，可以先平移到原点，旋转完，再平移回来），我们希望将向量 \(\vec{x}\) 绕旋转角旋转 \(\theta\) 度（从旋转轴正方向看去，进行逆时针旋转），变换到 \(\vec{x}'\)。对于任意旋转轴，可以用罗德里格斯公式求解旋转矩阵。

罗德里格斯公式的推导，采取拆分的思想，将旋转向量 \(\vec{x}\) 拆分成与旋转轴 \(\vec{a}\) 平行的分量 \(\vec{x}_{//}\) 和垂直分量 \(\vec{x}_{2D}\)，其中，\(\vec{x}_{//}\) 旋转前后不变，只需要考虑 \(\vec{x}_{2D}\) 的变化，如 图 12.4 所示：

(12.11)#\[\begin{split} \begin{aligned} \vec{x}' &= \vec{x}_{2D}' + \vec{x}_{//} \\ &= \vec{x}_{2D}\cos \theta + \vec{x}_{\perp} \sin \theta + \vec{x}_{//}\\ &= [(\vec{x} - (\vec{x} \cdot \vec{a})\vec{a}) \cos \theta] + (\vec{a} \times \vec{x})\sin \theta + (\vec{x} \cdot \vec{a}) \vec{a} \\ &= \cos \theta \vec{x} + (1-\cos \theta)(\vec{x} \cdot \vec{a}) \vec{a} + \sin \theta (\vec{a} \times \vec{x})\,. \end{aligned} \end{split}\]

我们可以直接推出轴角定义下的旋转矩阵：

(12.12)#\[\begin{split} \mathbf{R} = \cos \theta \mathbf{I} + (1 - \cos \theta) \mathbf{a}\mathbf{a}^T + \sin \theta \mathbf{a}^*,\,\mathbf{a}^* = \begin{bmatrix} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0 \end{bmatrix}. \end{split}\]

轴角表示法非常直观且紧凑，但有个很大的缺点是很难进行旋转的插值。假设我们有两个旋转 \((\vec{a}_0, \theta_0)\) 和 \((\vec{a}_1, \theta_1)\)，我们希望平滑地从 \((\vec{a}_0, \theta_0)\) 运动到 \((\vec{a}_1, \theta_1)\)，应该如何实现？如果我们采用的是欧拉角的表示，我们可以对三个旋转角度进行线性插值。但是对于轴角表示，旋转轴的插值并不直接。