19.3. 本章小结#
本章带领读者熟悉了运动学原理,也是主观动态中常用的数学部分,包括旋转的表示以及运动学概念。
在旋转的表示一节中我们主要介绍了旋转矩阵以及四元数。在前者的学习中我们首先通过简化版的二维情形带领读者熟悉矩阵表示的概念以及推导思路,随后进入到三维中的简化情形——绕坐标轴的旋转,接下来介绍了三维空间内两个坐标系之间的正交变换,最后我们推导出了绕定轴转动一定角度的三维旋转矩阵的具体形式。在后者的学习中我们仍然以二维情形开始介绍用复数表示二维旋转的方法,随后推广到四元数的概念及其运算并介绍了其所构成的数域,接下来详细推导了如何使用四元数表示三维旋转,最后介绍了四元数表示旋转最有用的应用之一——四元数插值。经过本节的学习,读者不仅要熟悉各种旋转表示本身的概念及使用方法,还要了解不同的表示之间的转换方式。
在运动学一节中我们介绍了前向运动学、关键帧动画以及逆向运动学。前向运动学是指给定铰链刚体各个关节的局部旋转以及关节间的连接关系和距离,求解每个关节相对于根关节位置的过程;这也是上一节所熟悉的数学工具的一项直接应用。关键帧动画则是结合了前向运动学与旋转插值的技术,实现了更低成本的主观动态的制作与生成。逆向运动学是一个与前向运动学相反的任务,即给定某关节的位置反解出每个关节的局部旋转的过程;我们介绍了循环坐标法、前向和后向迭代逆运动学以及雅可比矩阵法来求解这个问题,读者在掌握这些方法后不妨多思考一下每种方法的优劣以及适用场景。
19.3.1. 习题#
请查阅资料并回答问题:单位四元数和旋转矩阵之间如何互相转换?
考虑二维空间内如图 19.19 所示的一个铰链刚体,关节旋转角度分别为 \(\theta_0\sim\theta_2\),从根关节开始的每根骨骼长度分别为 \(l_0\sim l_2\),请用这些参数表示出末端(\(P_3\))位置,并求出末端位置关于这些参数的雅可比矩阵。
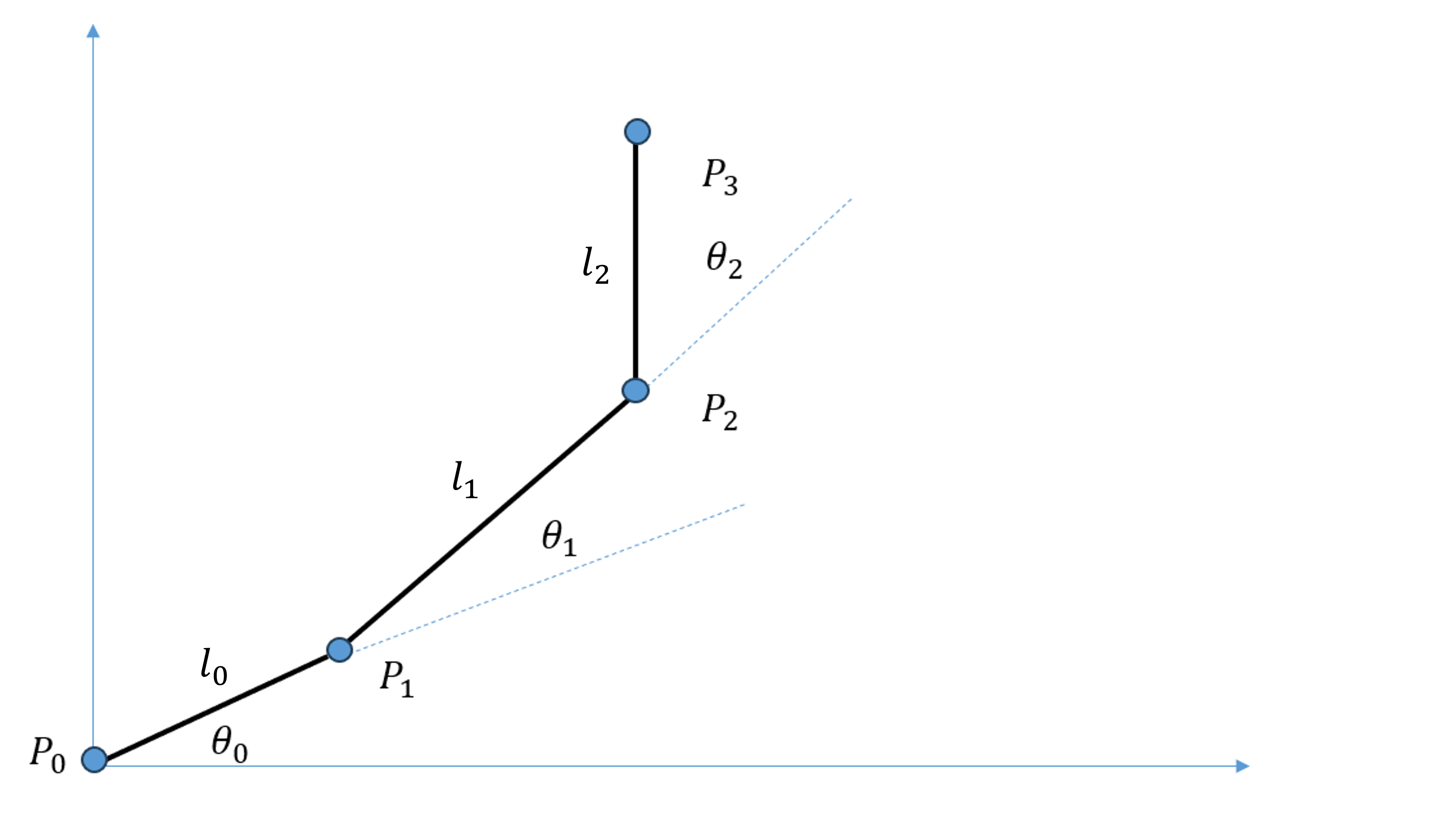
图 19.19 第 2 题图#
19.3.2. 参考文献#
无。