4.2. 多边形#
与绘制线不同,绘制多边形需要对多边形的内部进行填充。我们先从如何画一个纯色的多边形开始,再考虑如何在内部填充颜色。
4.2.1. 多边形的光栅化#
三角形是最简单的多边形,对于计算机图形学来说非常重要。任意一个二维多边形都可以切割成多个三角形的组合,同时三角形也是三维模型的重要组成部分(§8)。我们考虑绘制由 \(P_0=(x_0, y_0)\),\(P_1=(x_1, y_1)\),\(P_2=(x_2, y_2)\) 三个顶点定义的三角形,三个顶点保证逆时针顺序。在最简单的想法下,我们可以判断每个像素是否在三角形内部,如果是就绘制颜色,如代码 4.4 所示。
1def draw_triangle(x0: int, y0: int, x1: int, y1: int, x2: int, y2: int):
2 xmin, xmax = min(x0, x1, x2), max(x0, x1, x2)
3 ymin, ymax = min(y0, y1, y2), max(y0, y1, y2)
4 for x in range(xmin, xmax + 1):
5 for y in range(ymin, ymax + 1):
6 if inside(x, y, x0, y0, x1, y1, x2, y2):
7 draw(x, y)
那么如何判断点 \(P=(x,y)\) 是否在三角形内部?我们可以借助上一节提到的直线的隐式函数。如图 4.7 所示,我们规定边的方向为逆时针方向,也就是从 \(P_i\) 指向 \(P_{i+1}\)(\(P_2\) 指向 \(P_0\)),将其逆时针旋转 \(90^\circ\) 得到垂直于边的法向 \(N_i\),那么 \(N_i\) 一定指向三角形的内部。如果点 \(P\) 位于三条边的法向一侧,也就是代入三条边的隐式方程 \(F_i(P)\) 都大于 0,那么点 \(P\) 就位于三角形内部。反之如果有任意一条边的 \(F_i(P)<0\),那么点 \(P\) 就位于三角形的外部。
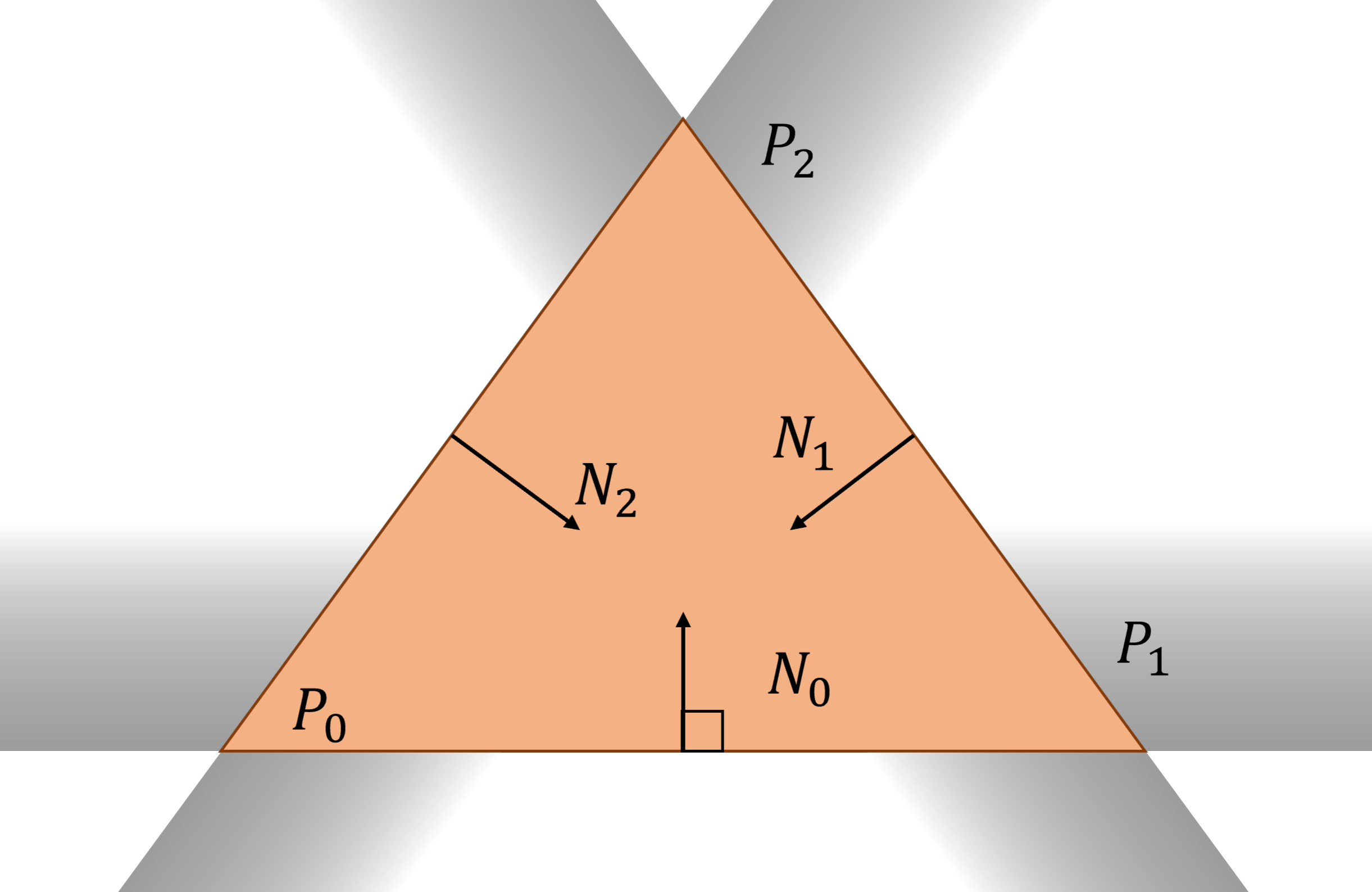
图 4.7 三角形内外检测#
这里我们遇到了和直线绘制中类似的情况。这个算法并没有什么问题,但是每个点都需要计算三次直线的隐式方程,包含整数乘法运算,有没有可能通过累加的方式避免乘法运算呢?观察最简单的三角形绘制算法,我们其实是在一行一行地绘制三角形中的像素。如果已知三角形在一行中的左边端点 \(y_L\) 和右边端点 \(y_R\),中间的像素其实没有必要进行内外检测,可以直接绘制。而维护左右端点的过程其实就是在绘制直线的过程。我们没有必要重复计算三条边与当前行的交点,而是可以通过上一行的交点和直线的斜率,增量更新到当前行的交点,这正是绘制直线的 DDA 算法。通过这种方式我们能够避免对所有像素进行三角形内外检测,而只通过增量更新的方法逐行绘制,这种算法被称为扫描线算法(Sweep-Line Algorithm)。这里我们仅在代码 4.5 中给出大致的伪代码。
1def draw_triangle(T):
2 for each edge pair:
3 initialize x_L, x_R
4 compute dx_L/dy_L, dx_R/dy_R
5 for each scanline at y:
6 for x in range(x_L, x_R + 1):
7 draw(x, y)
8 x_L += dx_L/dy_L
9 x_R += dx_R/dy_R
扫描线算法的想法可以自然拓展到多边形中。我们可以首先对多边形的所有边进行排序,然后用类似方法维护左右交点,从上到下进行扫描线的绘制。在面对多边形时,我们还要额外注意多边形非凸的情况。如图 4.8 所示,一条扫描线有可能和多边形有不只两个交点。为了处理这种情况,我们可以将所有边与扫描线的交点从左到右排序,可以发现第奇数交点到第偶数交点中间就是需要绘制的像素,而第偶数交点到第奇数交点之间是在多边形外部的区域。
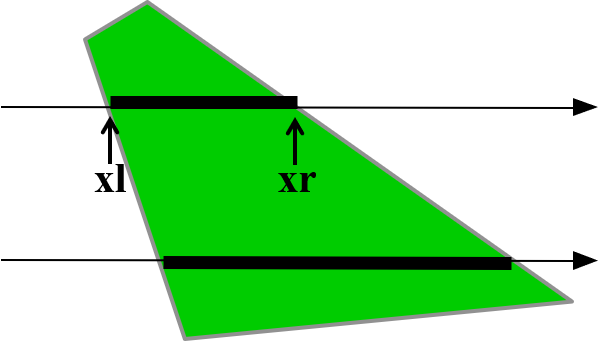
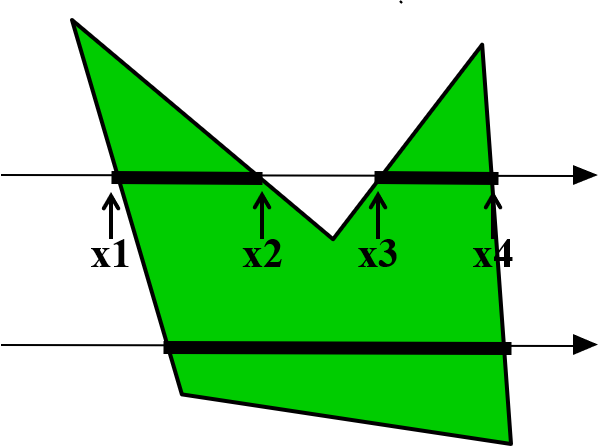
图 4.8 扫描线算法绘制填充多边形#
扫描线算法相比于简单的三角形算法更高效,然而在现代计算机上,其实使用的最多的是并行版的简单算法。这背后的原因在于,三角形在现代图形学中的地位非常重要,在后面 §14 的学习中我们会发现现代的渲染管线是完全围绕三角形搭建起来的,现代显卡的重要功能就是绘制三角形。为了能够快速绘制大量的三角形,现代显卡基本都会提供三角形内外检测的专门硬件模块,从而在硬件上实现并行的三角形绘制。
4.2.2. 颜色插值#
在上面介绍的算法中,我们只介绍了如何绘制纯色图形,在更一般的情况下我们希望在多边形内部填充不一样的内容,乃至为多边形内部的每个像素确定不同的颜色。比如,我们可以指定多边形各个顶点的颜色,然后在内部对顶点颜色进行插值,如图 4.9 所示。

图 4.9 三角形颜色插值:学习 OpenGL 的第一课 “hello triangle” 样例#
在绘制线段时,假设两个顶点 \((x_0, y_0)\) 和 \((x_1, y_1)\) 的颜色分别为 \(c_0\) 和 \(c_1\),那么 \((x, y)\) 像素点上的颜色可以通过线性插值得到:
当使用扫描线算法绘制多边形时,我们可以应用公式 (4.2) 在每一条横向扫描线内部插值,并且扫描线的两个端点的颜色可以再通过一次纵向边上的线性插值得到。因此,我们可以通过纵向横向两个方向的线性插值得到多边形内部的颜色,这样的方法称为双线性插值(Bi-linear Interpolation),如图 4.10 所示。
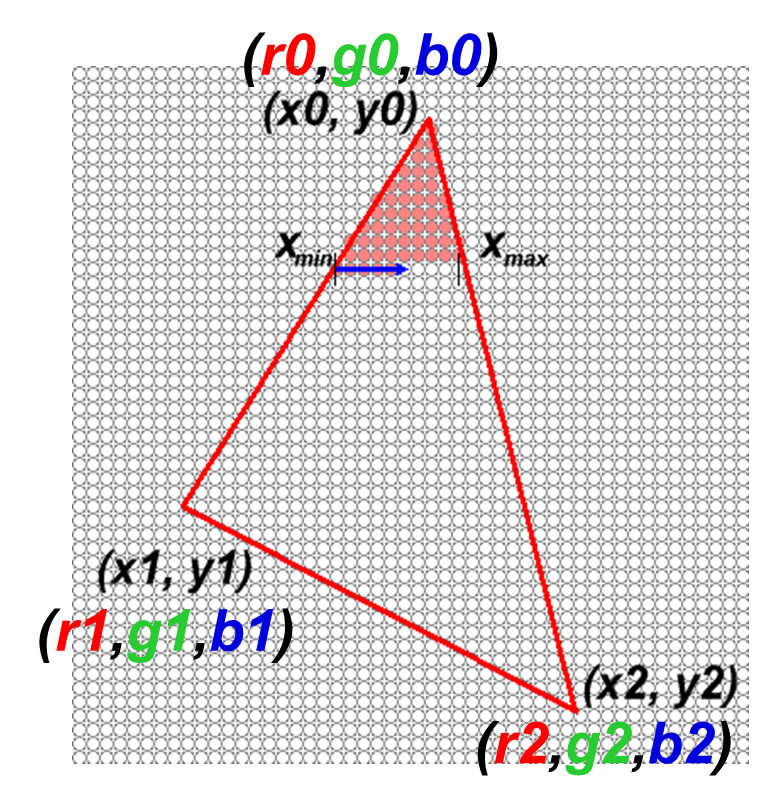
图 4.10 三角形双线性颜色插值#
上面的插值算法针对于扫描线算法,那么代码 4.4 中的简单三角形绘制算法应该如何插值颜色?在不使用扫描线时,我们直接绘制每个单独的像素,就需要确定每个像素相对于三角形三个顶点的权重,形式为:
\((\alpha, \beta, \gamma)\) 是我们要求的权重,类似于公式 (4.2) 中的 \((1-t, t)\)。\(\alpha + \beta + \gamma = 1\) 是权重的归一化条件。此外,我们还要求当像素点位于顶点 \((x_i, y_i)\) 时,对应的颜色 \(c=c_i\):比如在顶点 \((x_0, y_0)\) 上时,应有 \(\alpha=1\),\(\beta=0\),\(\gamma=0\)。这里我们直接给出满足这些要求的权重构造方法,称为重心坐标(barycentric coordinate)。
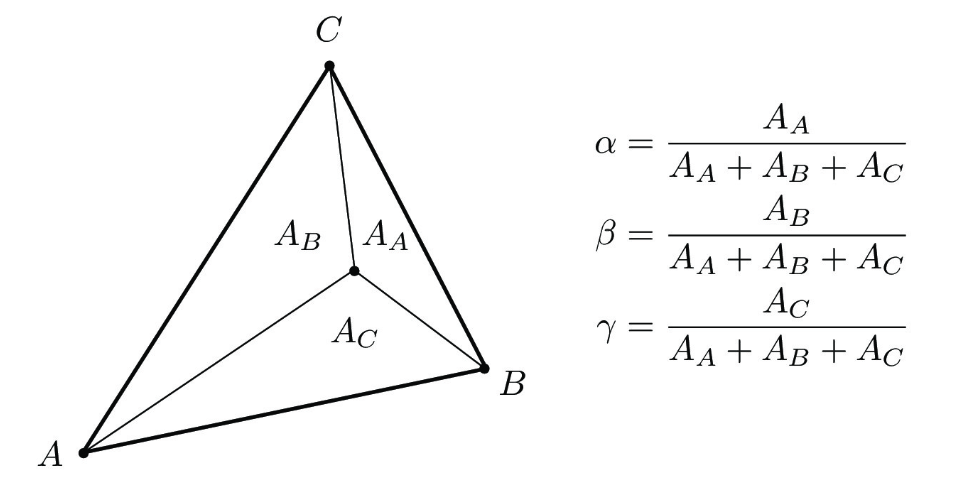
图 4.11 重心坐标插值#
如图 4.11 所示,\((\alpha, \beta, \gamma)\) 通过分割出的三个三角形的面积之间的比值确定:每个顶点的权重等于与顶点相对的三角形面积除以三角形总面积。这样的定义自然满足我们列出的要求:\(\alpha + \beta + \gamma = 1\),并且在顶点 A 处,\(\alpha=1\),\(\beta=0\),\(\gamma=0\)。此外,重心坐标也是线性的,意味着权重在三角形内部是均匀变化的:不管我们在三角形内部的任何一点上向右(或向上)移动一个像素,权重对应的改变始终是一个常数。我们把这个证明留作一个习题。
由于重心坐标插值和上面提到的双线性插值都是线性插值,它们其实是等价的。如何证明?首先,颜色的三个分量插值是相互独立的,我们可以单独考察其中一个分量,比如 R 通道。如果将 R 通道作为垂直于屏幕的 \(z\) 轴,将每个像素沿 \(z\) 轴平移对应的 R 值,我们就可以得到一个三维空间中的曲面。如果插值是线性的,这个曲面其实是一个倾斜的平面。而三个顶点是可以唯一确定空间中的一个平面,因此重心坐标插值和双线性插值是等价的。
4.2.3. 图像拉伸#
上面我们讨论了如何插值颜色,我们现在来看一下看起来稍微不一样的问题:如何像图 4.12 一样拉伸一个图像?

图 4.12 图像拉伸#
如果我们把拉伸的结果看成是对不规则四边形内部的填色,那么图像拉伸的问题就和上面介绍的颜色插值问题建立起了关联。区别在于,现在我们填充的颜色不再是顶点颜色插值得到,而是从原图像中查表得到。对应的问题就变成了,我们如何知道拉伸后每个像素对应原图像的哪个像素?解决方法其实非常简单。我们可以在原图像的空间中建立一个直角坐标系,每个顶点对应一个 \((u, v)\),一般直接称为 UV 坐标(UV coordinate)。拉伸图像之后,四个顶点和四条边上的 UV 坐标不会发生变化。我们使用上面介绍的颜色插值方法,在拉伸后的空间对 UV 坐标进行插值,可以得到每个像素对应的 UV 坐标,再回到原图像空间查找对应的像素就知道对应的颜色了。
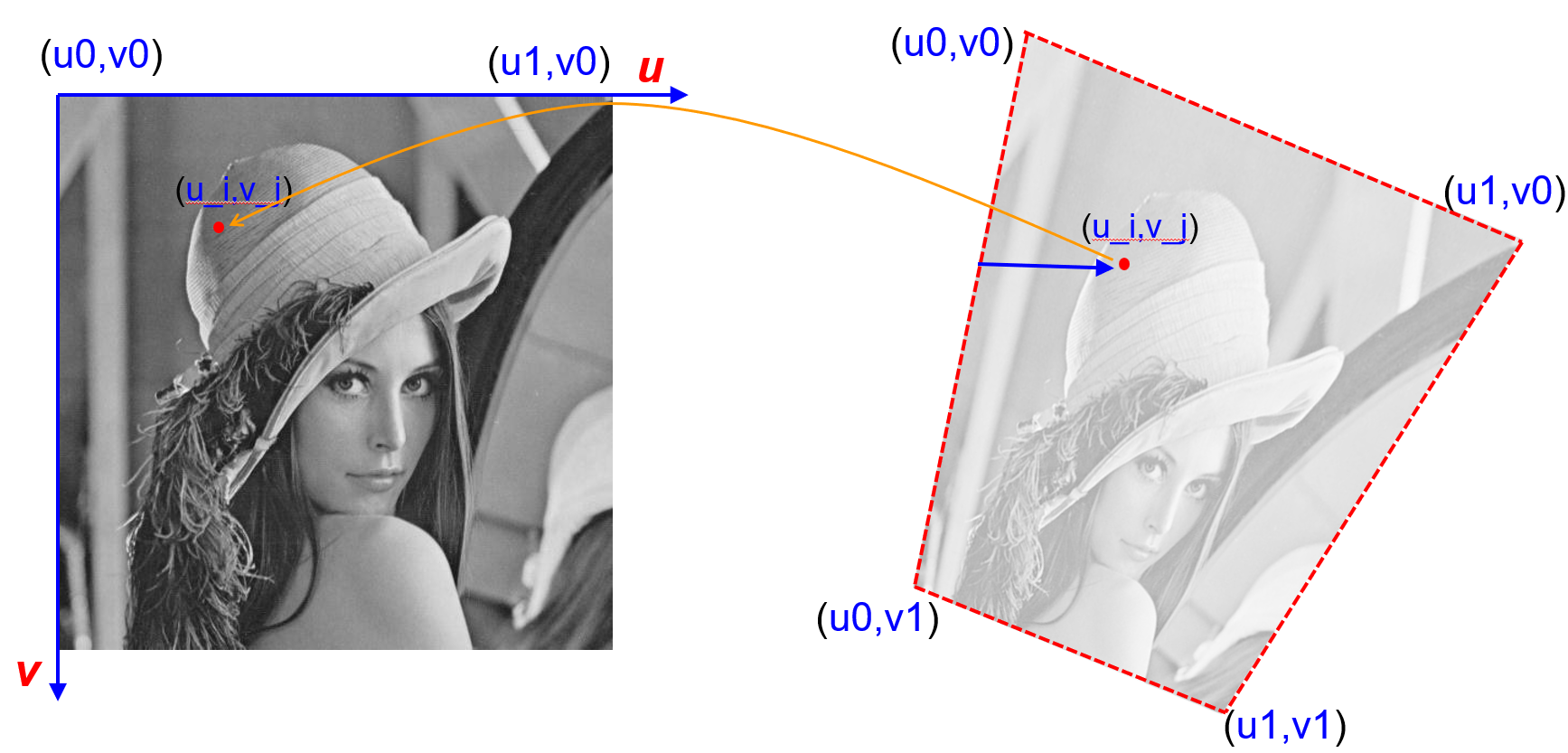
图 4.13 UV 映射#
一个需要注意的点是,尽管我们在上面证明了三角形的双线性插值和重心坐标方法是等价的,四边形没有唯一线性的插值方法。我们可以直接对四边形做双线性插值,或者将其分割成两个三角形分别使用重心坐标插值,得到的结果如图 4.14 所示。可以看到,两种方法插值的结果并不一致,颜色的占比不同。此外,这里演示的 UV 映射拉伸的方法是在二维中进行的,但是它还会在后面三维渲染的 §15 纹理章节中发挥巨大作用。
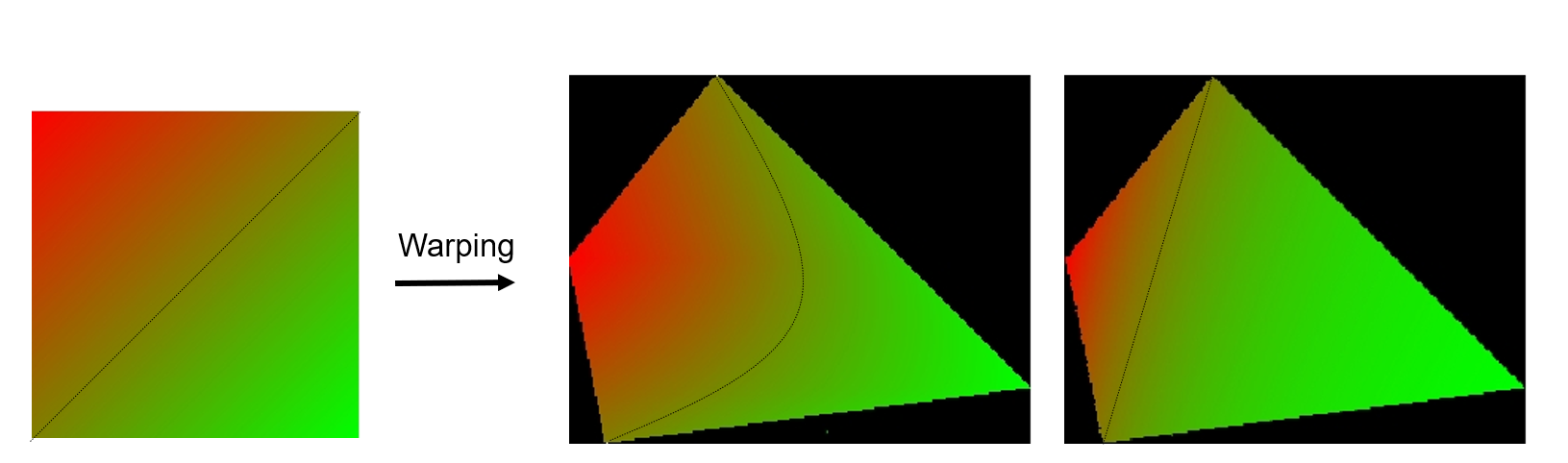
图 4.14 不同插值方法的结果#