图像分割与抠图

7.3. 图像分割与抠图#

大多数的图片都会有前景与背景，但是图片本身只有每个像素点的颜色信息，并没有告诉我们哪些部分是前景、哪些是背景。为了从颜色信息还原出前景与背景信息，就需要用到图像分割或者是抠图技术。对于一些前景背景界限分明的图像，每个像素要么只属于前景，要么只属于背景，从这种图像中恢复前景、背景的任务叫做图像分割（image segmentation），如图 7.19；即，求出一个与原图分辨率一致的二值图片，值为 0 的像素点属于背景，值为 1 属于前景。但对于更多数的图像来讲，前景与背景会有一定程度的混合，此时我们要求的对象就变成了一张透明度图像，每个像素点的值 (0 到 1 的实数) 反映的是前景颜色的占比，这个任务叫做抠图（image matting），如图 7.20。

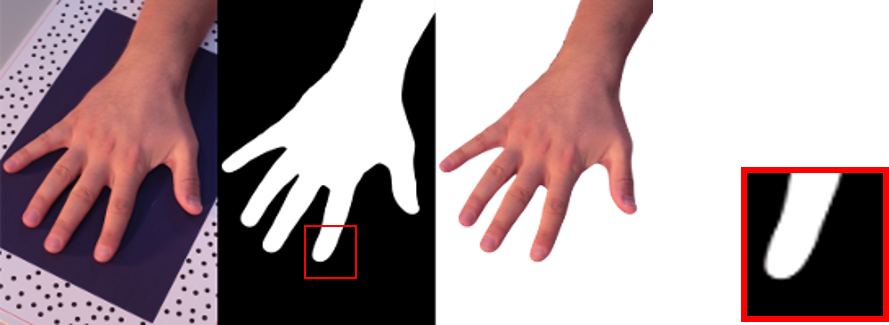
../../_images/segmentation-example.png

图 7.19 图像分割#

../../_images/matting-example.png

图 7.20 抠图#

不难看出，图像分割是抠图的一种特殊情况，接下来我们只关注抠图技术。我们首先形式化地表达抠图问题，然后介绍两种传统的解决方法，最后再介绍一些更智能的解决方法。

7.3.1. 问题描述#

令 \(\mathbf C\) 表示输入的图像，\(\mathbf F\) 表示前景图，\(\mathbf B\) 表示背景图，这些图都是 RGB 图像，\(\alpha\) 表示透明度 (或前景图的占比)，则它们之间的关系如下式：

(7.23)#\[ \mathbf C=\alpha\mathbf F+(1-\alpha)\mathbf B \]

对于某一个像素点 \(i\)，就是要解如下方程：

(7.24)#\[\begin{split} \begin{aligned} \mathbf C_i^R&=\alpha_i\mathbf F_i^R+(1-\alpha_i)\mathbf B_i^R\\ \mathbf C_i^G&=\alpha_i\mathbf F_i^G+(1-\alpha_i)\mathbf B_i^G\\ \mathbf C_i^B&=\alpha_i\mathbf F_i^B+(1-\alpha_i)\mathbf B_i^B \end{aligned} \end{split}\]

其中 \(\alpha_i,\mathbf F_i^R,\mathbf F_i^G,\mathbf F_i^B,\mathbf B_i^R,\mathbf B_i^G,\mathbf B_i^B\) 为未知量，\(\mathbf C_i^R,\mathbf C_i^G,\mathbf C_i^B\) 为已知量。这是一个欠定的线性方程，有无穷多组解。

7.3.2. 传统的解决方法#

对于欠定方程，我们有两种求解的思路，一个是减少未知量个数，一个是增加方程的数量。这两种方法分别对应于蓝 (绿) 幕抠图（blue (green) screen matting） 和三角抠图（triangulation matting），它们都是在特定拍摄环境下使用的算法，简易但是有较大的局限性。

7.3.2.1. 蓝 (绿) 幕抠图#

这项技术在影视界应用较多，拍摄时用一片蓝幕作为背景板（绿幕同理，如图 7.21），那么在处理时就可以假设背景图只有蓝色分量，另外还要假设前景图没有蓝色分量，即 \(\mathbf F_i^B=\mathbf B_i^R=\mathbf B_i^G=0\)，并且我们还能够知道背景的蓝色分量 \(\mathbf B_i^B\) 的值。于是未知量只剩下 3 个，方程组 (7.24) 变为：

(7.25)#\[\begin{split} \begin{aligned} \mathbf C_i^R&=\alpha_i\mathbf F_i^R\\ \mathbf C_i^G&=\alpha_i\mathbf F_i^G\\ \mathbf C_i^B&=(1-\alpha_i)\mathbf B_i^B \end{aligned} \end{split}\]

这样，未知量与方程个数相等，可以求出唯一解。

../../_images/blue_screen_matting.png

图 7.21 绿幕抠图#

我们假设前景没有蓝色分量的原因在于，人身上的色调主要是红色和黄色，蓝色和绿色很少出现。由于限制众多，这个方法的缺陷也很明显：

  • 前景中不可以有蓝色，否则前景的某些区域也会被当成背景从而丢失。这也意味着蓝幕抠图不能应用到透明物体上。

  • 蓝色背景所反射的光可能会打到前景图上，造成扣取出的前景图边缘偏蓝 (如图\ref{fig:blue_screen_matting-reflection}所示)。

../../_images/blue_screen_matting-reflection.png

图 7.22 蓝色背景反射到前景后对蓝幕抠图的影响#

7.3.2.2. 三角抠图#

仅一张彩色图片提供的信息不足，所以这项技术通过对同样的前景物体配上两组不同的、已知的背景图分别拍摄以弥补这个不足。记另外一张背景图为 \(\hat{\mathbf B}\)，其与前景一起拍摄得到的图片为 \(\hat{\mathbf C}\)，则方程组变为：

(7.26)#\[\begin{split} \begin{aligned} \mathbf C_i^R&=\alpha_i\mathbf F_i^R+(1-\alpha_i)\mathbf B_i^R\\ \mathbf C_i^G&=\alpha_i\mathbf F_i^G+(1-\alpha_i)\mathbf B_i^G\\ \mathbf C_i^B&=\alpha_i\mathbf F_i^B+(1-\alpha_i)\mathbf B_i^B\\ \hat{\mathbf C}_i^R&=\alpha_i\mathbf F_i^R+(1-\alpha_i)\hat{\mathbf B}_i^R\\ \hat{\mathbf C}_i^G&=\alpha_i\mathbf F_i^G+(1-\alpha_i)\hat{\mathbf B}_i^G\\ \hat{\mathbf C}_i^B&=\alpha_i\mathbf F_i^B+(1-\alpha_i)\hat{\mathbf B}_i^B \end{aligned} \end{split}\]

其中 \(\alpha_i,\mathbf F_i\) 为未知量，\(\mathbf C_i,\mathbf B_i,\hat{\mathbf C}_i,\hat{\mathbf B}_i\) 为已知量，这是一个具有 4 个未知量、6 个方程的超定线性方程组，可以使用最小二乘法求解。

这个方法不再要求前景物体不能包含蓝色分量，不要求背景必须是蓝色，也可以处理透明物体，但是它要求拍摄两张图片的时候前景物体相对相机的位置必须保持一致。

../../_images/triangulation_matting.jpg

图 7.23 三角抠图的结果#

7.3.3. 贝叶斯抠图#

前面提到，传统的方法需要特定的拍摄条件，并且可能会存在各种各样不能处理的特殊情况；贝叶斯抠图（Bayesian matting） 是更智能的抠图算法，用户需要提供一张额外的三值图 (trimap)，该图的每个像素点有三种取值，分别表示前景、背景和未知，如图 7.24 所示。

../../_images/bayesian-trimap-original.jpg
../../_images/bayesian-trimap-trimap.jpg
../../_images/bayesian-trimap-result.jpg

图 7.24 用户提供三值图以辅助算法完成抠图任务#

记输入的原图为 \(\mathbf C\)，抠图结果为标量场 \(\alpha\)，前景图为 \(\mathbf F\)，背景图为 \(\mathbf B\)。我们的问题是，给定三值图，求解未知区域的最大似然：

(7.27)#\[ \max_{\alpha,\mathbf F,\mathbf B}P(\alpha,\mathbf F,\mathbf B\mid\mathbf C) \]

优化目标是一个后验概率，即已知观测结果 \(\mathbf C\) 后 \(\alpha,\mathbf F,\mathbf B\) 的概率，由贝叶斯公式有：

(7.28)#\[ P(\alpha,\mathbf F,\mathbf B\mid\mathbf C)=\frac{P(\mathbf C\mid\alpha,\mathbf F,\mathbf B)P(\alpha,\mathbf F,\mathbf B)}{P(\mathbf C)} \]

其中 \(P(\mathbf C)\) 是常数，并且为了简化问题，假设 \(P(\alpha)\) 也是常数，且 \(\alpha,\mathbf F,\mathbf B\) 相互独立，为计算方便对 (7.28) 右手项取对数，得到

(7.29)#\[ \arg \max_{\alpha,\mathbf F,\mathbf B}P(\alpha,\mathbf F,\mathbf B\mid\mathbf C)=\arg \max_{\alpha,\mathbf F,\mathbf B}[\ln P(\mathbf C\mid\alpha,\mathbf F,\mathbf B)+\ln P(\mathbf F)+\ln P(\mathbf B)] \]

接下来就是估计式 (7.29) 中目标函数的每一项了，我们假设三个分布 \(P(\mathbf C\mid\alpha,\mathbf F,\mathbf B)\), \(P(\mathbf F)\), \(P(\mathbf B)\) 都是高斯分布，所以我们现在只需分别确定的它们的均值和方差。以下我们都假设每个像素点互相独立，所以后续的公式都是针对单个像素的值，并且为了记号简便我们省去下标。

对于第一个分布 \(P(\mathbf C\mid\alpha,\mathbf F,\mathbf B)\)，根据式 (7.23) 可知 \(\mathbf C\) 的均值为 \(\alpha\mathbf F+(1-\alpha)\mathbf B\)，我们假设这个分布是各向同性的，所以其方差为一个用户可调节的参数 \(\sigma_c^2\)。所以

(7.30)#\[ P(\mathbf C\mid\alpha,\mathbf F,\mathbf B)=\frac 1{(2\pi)^{3/2}\sigma_c^3}\exp\left\{-\frac 1{2\sigma_c^2}\|\mathbf C-[\alpha\mathbf F+(1-\alpha)\mathbf B]\|^2\right\} \]

第二个和第三个分布完全类似，都是先验分布，我们以前景的分布 \(P(\mathbf F)\) 为例，它可以写成如下形式：

(7.31)#\[ P(\mathbf F)=\frac 1{(2\pi)^{3/2}\|\Sigma_\mathbf F\|^{1/2}}\exp\left\{-\frac 12(\mathbf F-\mu_\mathbf F)^\top\Sigma_\mathbf F^{-1}(\mathbf F-\mu_\mathbf F)\right\} \]

其中 \(\mu_\mathbf F\) 和 \(\Sigma_\mathbf F\) 是通过采样估计的。具体来讲，对于一个像素，记它邻域范围内所有三值图标记为前景的像素点集合为 \(\mathcal N_\mathbf F\) (此处的邻域可以是以该像素点为中心的圆形或矩形窗口)，则均值与方差表示为：

(7.32)#\[\begin{split} \begin{aligned} \mu_\mathbf F&=\frac 1W\sum_{i\in\mathcal N_\mathbf F}w_i\mathbf F_i\\ \Sigma_\mathbf F&=\frac 1W\sum_{i\in\mathcal N_\mathbf F}w_i(\mathbf F_i-\mu_\mathbf F)(\mathbf F_i-\mu_\mathbf F)^\top \end{aligned} \end{split}\]

其中 \(w_i\) 为对邻域内采样点的权重，\(W=\sum_{i\in\mathcal N_\mathbf F}w_i\) 为权重之和；权重的选取与像素点的透明度和高斯分布有关，即 \(g_i\) 为像素点 \(i\) 在以当前像素为中心、方差为 8 的高斯分布上的取值，则 \(w_i=\alpha_i^2g_i\) (对于背景颜色，权值选取为 \(w_i=(1-\alpha_i)^2g_i\))。

将这三个分布的形式代入式 (7.29)，可以得到一个关于 \(\alpha,\mathbf F,\mathbf B\) 的目标函数，分别对每个量求偏导可以得到最大似然解。但是直接求导后会出现含有 \(\alpha\mathbf F\) 和 \(\alpha\mathbf B\) 这样的二次项，不好直接求解，所以我们采用迭代法求解：先固定 \(\alpha\) 并求解 \(\mathbf F\) 和 \(\mathbf B\) 使目标函数取极值，然后固定 \(\mathbf F\) 和 \(\mathbf B\) 并求解 \(\alpha\) 使目标函数取极值，重复这个过程直到收敛。具体的计算公式这里不再推导，可以参考 [CCSS01]。贝叶斯抠图的效果见图 7.25。

../../_images/bayesian-results.png

图 7.25 贝叶斯抠图效果#