4.1. 光栅化#
由于屏幕被划分为了一个个像素,将几何体绘制到屏幕上的过程就像是往一个个格子里填颜料的过程,如图 4.3 所示。这个过程被称为光栅化(rasterization):将连续表达的几何图形转换成离散的图像表达。光栅化的概念会一直延申到三维绘制,也就是 §13 渲染中,不过在那里语义可能稍微发生一些变换。
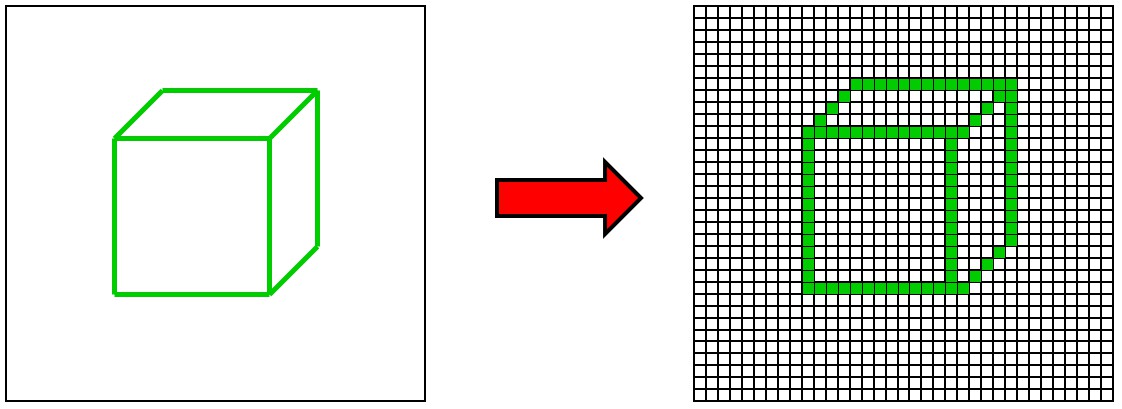
图 4.3 将连续的几何形状(左图)转换为离散的图像表达(右图)的过程被称为光栅化#
下面我们从直线开始介绍最经典的光栅化算法。
4.1.1. 直线的光栅化#
假设我们有一块\(N\)行\(M\)列的屏幕,在屏幕空间里我们建立坐标系,左下角像素中心为零点,右上角像素中心的坐标为\((M-1,N-1)\),在这个坐标系中我们希望绘制方程为\(y(x)=mx+b\)的直线段,从\((x_0, y_0)\)到\((x_1, y_1)\),满足\(y_0=m x_0+b\),\(y_1=mx_1+b\)。为了讨论方便,我们首先假设\(0<m<1\),并且\(x_0 < x_1\),在最后再考虑其他情况的处理。最终实现的效果如图 4.4 所示。
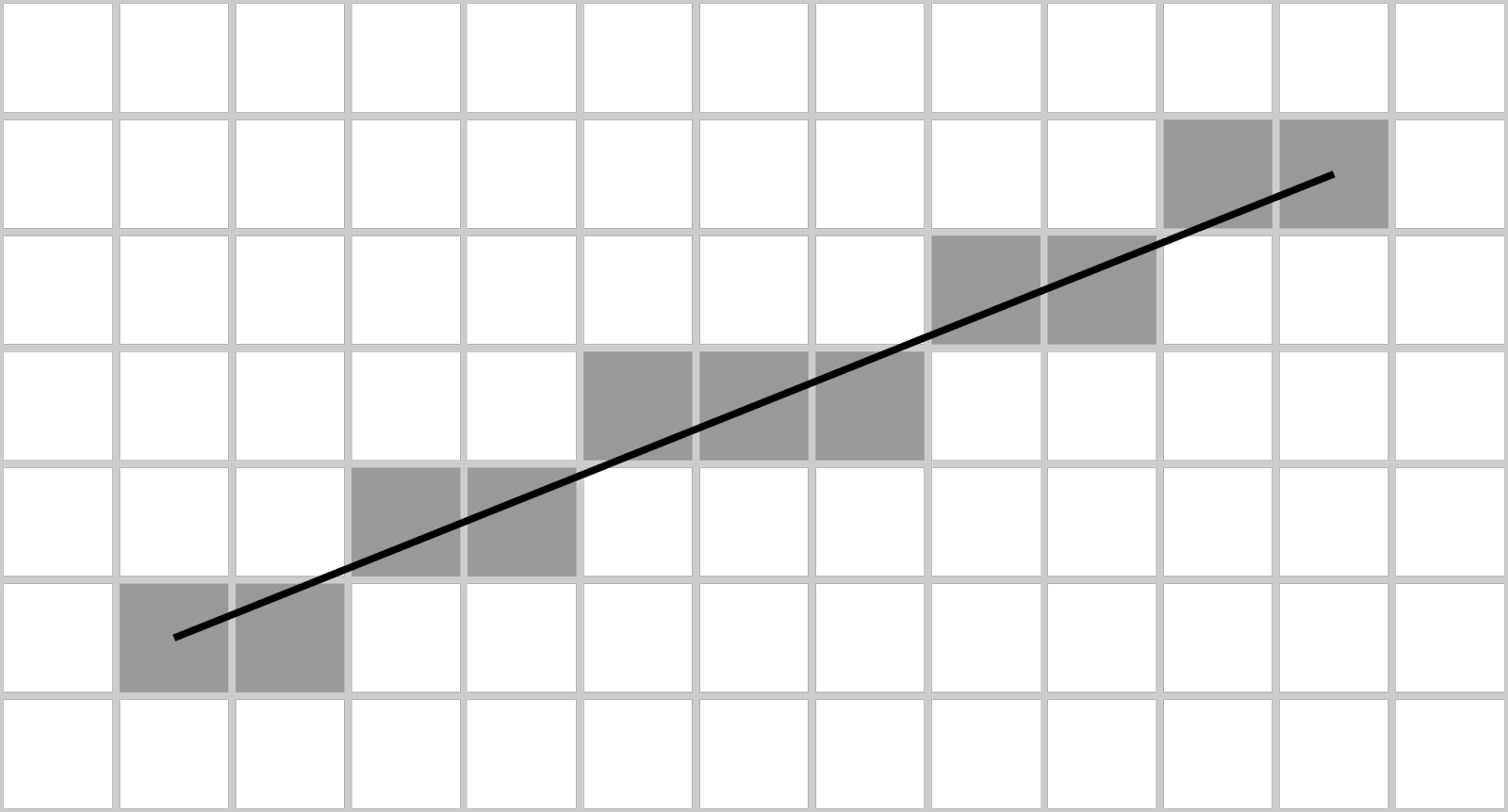
图 4.4 直线的光栅化#
在最简单的想法下,我们可以遍历横坐标从\(x_0\)到\(x_1\),根据方程计算出对应的\(y\),然后绘制对应像素,如代码 4.1 所示。
1def draw_line(x0: int, x1: int, m: float, b: float):
2 for x in range(x0, x1 + 1):
3 y = m * x + b
4 draw_pixel(x, Round(y))
这样做并没有任何错误,但是效率可以进一步提高。一种思路是并行循环,但是这样的话画一条直线我们就得占用多线程资源,并且每个线程的任务过于简单。考虑到我们往往要同时绘制很多条直线,这样显然不是效率最高的做法。于是我们得更细致地分析算法的耗时来寻找提升的空间。在计算每个像素的位置时,我们主要的时间花费在了浮点数乘法、加法以及取整运算。由于我们是等间隔采样直线上的点,自然想到可以使用累加代替乘法操作,这样就得到了绘制直线的 DDA(Differential Digital Analyzer) 算法,如代码 4.2 所示。
1def draw_line(x0: int, y0: int, x1: int, y1: int):
2 y = y0
3 m = (y1 - y0) / (x1 - x0)
4 for x in range(x0, x1 + 1):
5 draw_pixel(x, Round(y))
6 y += m
在 DDA 算法中,我们成功在循环中去掉了浮点数乘法操作,仅保留了加法和取整,自然相比于代码 4.1 要更快。那么我们是否达到了最优的直线光栅化算法呢?一个重要的观察是,尽管直线方程是用实数表示的方程,但是我们最终只需要在屏幕上画出离散的像素点,这些像素的点的位置是可以只用整数进行表示的。由于浮点数的表示和精度问题,浮点数的运算时间通常是要比整数更慢的,在早期的计算机上尤为明显。我们有没有可能构造出只有整数运算的程序?
4.1.2. 布雷森汉姆直线算法#
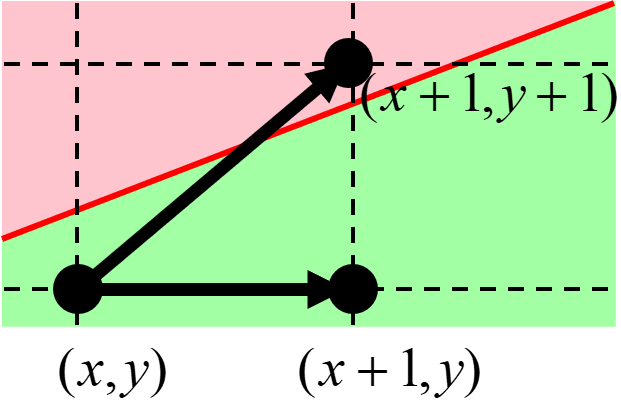
布雷森汉姆教授(Jack Elton Bresenham)在1962年提出了著名的布雷森汉姆直线算法(Bresenham’s Line Algorithm),能够在每个像素点上只计算整数加减法的情况下获得和 DDA 算法相同的结果。与 DDA 算法一样,布雷森汉姆直线算法的核心也是累加。观察图 4.5 ,如果我们已经在 \((x,y)\) 处(这里 \(x\),\(y\) 均为整数)画出了一个像素,那么累加的核心目的,就是确定下一个像素是画在 \((x+1, y)\) 处还是 \((x+1, y+1)\) 处。也可以从图 4.4 中观察到,如果我们限制了 \(0<m<1\),那么直线光栅化的结果其实是用一段一段的短水平线近似整条斜线。算法的核心,就是给出何时应该在 \(y\) 上加 \(1\)。
图 4.5 布雷森汉姆直线算法原理图#
那么接下来的问题自然就是:判断是否在 \(y\) 上加 \(1\) 的标准是什么?布雷森汉姆直线算法使用了一个非常符合直觉的判据:当点 \((x+1,y+1/2)\) 位于直线的上方时,我们应该选择像素点 \((x+1,y)\),反之选择 \((x+1,y+1)\)。注意我们说的 \((x, y)\) 指的是像素中心,\((x+1, y+1/2)\) 是以 \((x+1, y)\) 为中心的像素的上边中点。如果点 \((x+1,y+1/2)\) 位于直线的上方,说明直线的大部分还在 \((x+1, y)\) 这个像素内,于是我们就不用在 \(y\) 上加 \(1\);否则,直线的大部分已经在 \((x+1, y)\) 这个像素外边了,我们就得在 \(y\) 上加 \(1\)。由于 \(0<m<1\) 的限制,我们能够保证当 \(x\) 加 \(1\) 时,\(y\) 最多加 \(1\),因此只有我们上面说的两种情况。
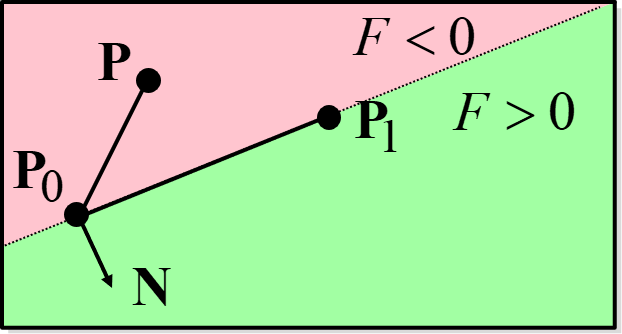
算法的流程确定了,剩下的就是数学推导。为了判断点在直线的上方还是下方,我们引入直线的隐式方程。如图 4.5 所示,对于从 \(P_0\) 到 \(P_1\) 的直线,我们将 \(P_1 - P_0\) 这个矢量顺时针旋转 \(90^\circ\) 得到法向 \(N\) 垂直于直线,对于任意一个点 \(P\),定义直线的隐式方程为 \(F(P)=N\cdot(P-P_0)\)。称其为隐式方程,是因为 \(F(P)=0\) 这个方程的解就是经过 \(P_0\) 和 \(P_1\) 的这条直线。并且由几何性质可知,当 \(F(P)>0\) 时,\(P\) 在 \(N\) 的同侧,也就是直线的下方;当 \(F(P)<0\) 时,\(P\) 在 \(N\) 的异侧,也就是直线的上方。注意到把 \(P=(x+1, y+1/2)\) 代入到 \(F(P)\) 中时,我们还是需要乘法运算。而为了避免乘法,就需要对 \(F(P)\) 进行累加。具体来说,如果我们已知 \(F(P)\) 的值,那么 \(F(P+\Delta)\) 可以表示为:
在使用公式 (4.1) 时,\((x+1,y+1/2)\),\((x+1,y)\),\((x+1,y+1)\) 相对于 \((x,y)\) 的 \(\Delta\) 都是定值,分别是 \((1,1/2)\),\((1,0)\),\((1,1)\);\(N\) 也是定值,因此 \(N\cdot \Delta\) 是定值,这个乘积可以预先计算,循环中只需要考虑累加。并且,为了保证 \(F(P+\Delta)\) 只会产生整数结果,我们可以选择 \(N=(2(y_1-y_0), -2(x_1-x_0))\),这样既能保证垂直,又能保证在 \(\Delta=(1,1/2)\) 时 \(N\cdot \Delta\) 还是整数。
总结一下,我们得到了最终的布雷森汉姆直线算法,如代码 4.3 所示。可以观察到,循环中只剩下整数加法和一个分支。
1def draw_line(x0: int, y0: int, x1: int, y1: int):
2 y = y0
3 dx, dy = 2 * (x1 - x0), 2 * (y1 - y0)
4 dydx, F = dy - dx, dy - dx // 2
5 for x in range(x0, x1 + 1):
6 draw_pixel(x, y)
7 if F < 0:
8 F += dy
9 else:
10 y += 1
11 F += dydx
最后我们还剩下了一点东西没有讨论,就是 \(0<m<1\) 的限制条件。这个条件保证了在x坐标增加 1 时,y坐标最多只需要增加 1,可以想象当 \(m>1\) 时,有可能x坐标增加 1,我们需要在竖直方向连续画多个像素。为了画出任意方向的直线,我们需要将斜率按照图 4.6 的八种情况进行分类讨论。在每种情况中,我们选择直线最贴近的坐标轴进行遍历,并考虑另外一个坐标轴需要累加还是累减,但算法的本质并没有任何区别。这里我们就不给出完整的八种情况的布雷森汉姆直线算法,留给读者自行实现。
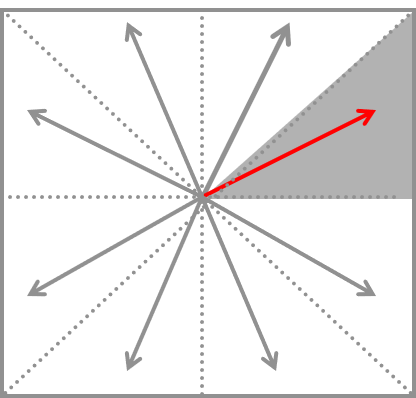
图 4.6 布雷森汉姆直线算法依据斜率不同的变体#
布雷森汉姆直线算法是最经典、应用最广泛的直线光栅化算法,但是也不是唯一的直线算法。在上面的讨论中,我们默认线的宽度为一个像素,Alan Murphy 在 1978 年对布雷森汉姆直线算法做出了改进[1],使之能够绘制有宽度的直线。吴小林教授在 1991 年提出的吴小林直线算法(Xiaolin Wu’s Line Algorithm) [Wu91] 可以实现带反走样的直线光栅化。我们将在 §5 重点介绍反走样这一概念。
画直线的方法还能自然推广到画圆中。我们已知圆的隐式函数为 \(F(P)=|P-P_0|^2 - r^2\),因此可以尝试用类似布雷森汉姆直线算法中的累加方法绘制圆,这一过程与布雷森汉姆直线算法类似,在 Wikipedia 中也有具体推导[2]。