10.2. 点云的表面重建#
尽管点云的数据表示可以方便地从深度传感器中获取,然而相比于此前介绍的网格模型等三维表示方式,点云格式仍然存在较大的局限。如 图 10.3 为北京大学静园五院大门处重建得到的三维点云,该点云包含超过 10,000 个点,模型大小已经达到大约 150MB,即使如此,在图像中仍然存在明显的、因为点云不够致密而产生的孔隙,表明点云在表征场景外观时具有较大局限性;除此之外,点云本身是无序的、非结构化的,其对几何形状的表达也是隐式的(不同于网格模型,点云仅仅隐含了对象的几何形状,而将其非显式地建模出来),这导致在点云上进行计算和处理将困难重重。

图 10.3 北京大学静园五院大门处重建得到的三维点云。#
因此,点云通常经过表面重建(surface reconstruction)的方法转化为网格(mesh)的形式来表示。有时点云的表面重建也称作网格化(meshing)。我们将介绍两种主要的表面重建方法:
德劳内三角剖分(Delaunay Triangulation)
泊松表面重建(Poisson Surface Reconstruction)
10.2.1. 德劳内三角剖分#
在三维空间中,三角剖分(triangulation)是指将点云转化为三角形网格(triangle Mesh)的过程。如 图 10.4,由于点集本身的无序性,在给定的点集上构建三角形网格并没有唯一的方法。
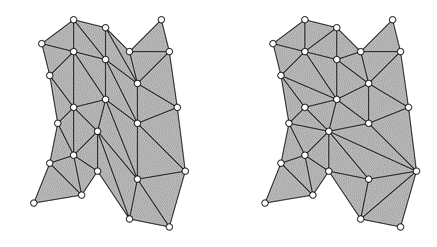
图 10.4 对同样点集进行不同的三角剖分。#
然而,直觉上来说,我们也并不希望任意地连接点云中的点,来将其转化为三角网格。例如,我们希望避免连接过远的两个点,或是希望避免网格自相交。为此,我们提出某种标准来评价三角剖分的质量,从而能够归纳出一种相对“合理”的三角剖分方法来将点云转化为三角网格。一种直观的想法就是:尽量生成较为“均匀”的三角形。德劳内三角剖分就适用于此,它能够找到一种方法,最大化三角剖分结果中最小的角,从而得到尽量“均匀”的三角网格。
简便起见,我们以二维情况下的德劳内三角剖分为例。严格意义上来说,德劳内三角剖分并不是一种算法,而是指一类满足了特定条件的三角剖分。这个条件就是:生成结果中,任何三角形的外接圆内,都不包含任何点。可以证明,这样的三角剖分最大化了“所有三角形中最小的内角”。
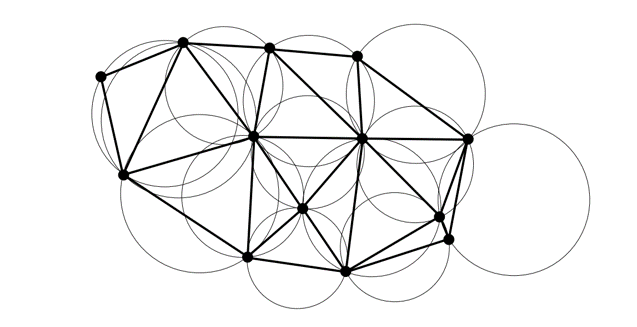
图 10.5 平面上十个点的德劳内三角剖分结果,通过画出每个三角形的外接圆,可以看到任何一个外接圆内都不包含点。#
根据德劳内三角剖分的性质,结合三角形外接圆的性质,我们很容易可以得出一个准则: 任何一对存在共用边的三角形(图 10.6),必须满足 \(\alpha+\gamma<180\deg\),否则就不满足德劳内三角剖分的性质。 此外,我们还可以得到一个推论:为了恢复这种性质,我们只需要把 \(BD\) 之间的边删去,加上 \(AC\) 之间的边。
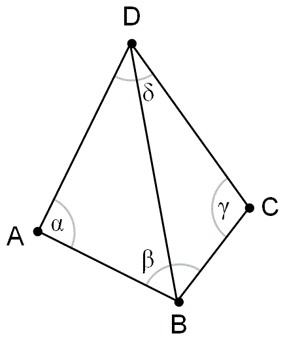
图 10.6 共边三角形。#
这种“翻转”的思路就产生了一个非常简单的算法:
构造任意三角剖分,然后检查共边三角形。
如果不满足性质,就进行翻转,重新连接边。
重复检查其他三角形对,直到所有三角形对都满足性质。
遗憾的是这种最简单的算法并不高效,可能需要检查 \(\Theta(n^2)\) 次。一个可能的改进是将算法改为增量式进行,每次向当前集合中添加一个点并连接一些边组成三角形,随后检查受到影响的周围的三角形是否满足德劳内性质,并对不满足性质的三角形进行翻转。这样的算法仍然需要检查 \(O(n^2)\) 次。
这些基于翻转的算法始终难以并行化。另一种进行德劳内三角剖分的思路是采用分治算法:在这种算法中,我们每次递归地画一条线,将点集分成两个子集。为每一个子集递归地进行三角剖分,然后沿分割线合并这两组。利用一些巧妙的技巧,合并操作可以在 \(O(n)\) 时间内完成,所以总的运行时间是 \(\Theta(n\log n)\)。基于这种分治算法进行的后续改进可以将时间进一步减少到 \(O(n\log\log n)\) [Dwy87]。
10.2.2. 泊松表面重建#
与德劳内三角剖分这种从点云直接构造三角网格的方法相比,泊松表面重建则另辟蹊径,采用了一种相对间接的方式来完成点云到网格的转换。
不难想见,德劳内三角剖分这一类直接方法存在一定的隐患:当输入的点云数据中包含噪声,或者含有一些错误的点集时,由于三角剖分必然会构造以噪点和错误点为顶点的三角形,这将不可避免地导致视觉上异常的结果。
泊松表面重建则并不直接构造三角网格,而是首先通过构建符号距离函数(Signed Distance Function,SDF)这一隐式表示,然后再通过行进立方体(Marching Cubes)算法,从符号距离函数场中提取出三角网格。
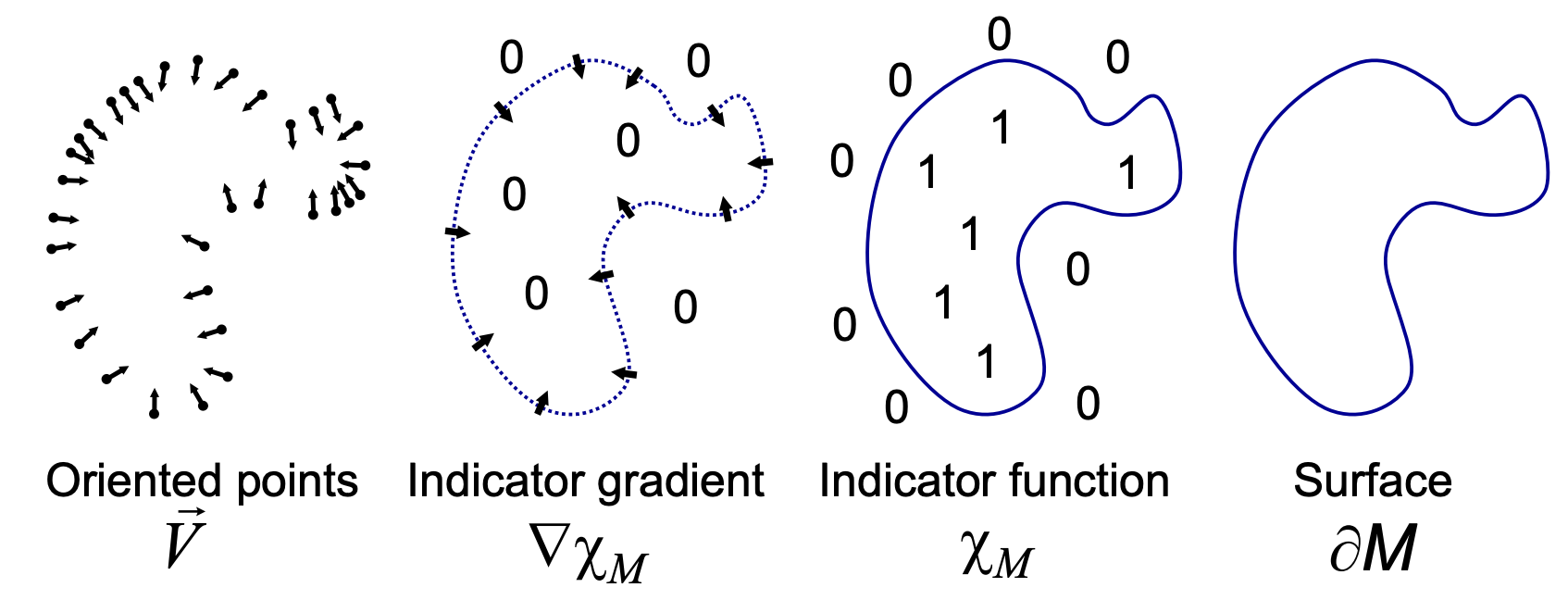
图 10.7 泊松表面重建原理。#
具体来说,泊松表面重建基于这样一个观察:如 图 10.7,对于一个空间中的实体 \(M\),如果我们定义一个指示函数 \(\chi_M\) 来标识其表面 \(\partial M\),内部的点都具有 \(1\) 的函数值,外部的点都具有 \(0\) 的函数值,那么该指示函数的梯度场 \(\nabla \chi_M\) 就只在 \(\partial M\) 上具有非零梯度。而表面上某一点梯度的方向与该点的法向量恰好反向,因此一个带有法向量的点云 \(\vec V\) 可以被看作是 指示函数梯度场在边界上的一个采样。因此,当我们可以通过 \(\vec V\) 估计出指示函数的梯度场时,问题就转化为如何从一个函数的梯度场恢复出原函数,即从下式中估计 \(\chi_M\):
然而由于等式右端的向量场不一定可积(例如有可能并不是无旋的),因此我们无法找到一个精确解,而需要将上式通过泊松方程转化为可以估计最小二乘解的形式:
最终得到指示函数的近似估计。因此,泊松表面重建依赖带有法向量信息的点云数据作为输入。算法通过八叉树(octree)组织这些带法向量信息的点并在八叉树节点上定义一系列基函数,通过求解上述泊松方程得到基函数之间组合的系数,从而最终拟合出指示函数。由于使用了平滑滤波器来进行近似求解,得到的指示函数在表面附近具有类似符号距离函数的性质,因此通过 §9.3.5 中介绍的行进立方体算法可以从等值面中提取出三角网格,就得到了最终的网格表示。
如 图 10.8 所示 ,泊松表面重建具有鲁棒性好、生成表面平滑的优点。

图 10.8 泊松表面重建的效果。#
泊松表面重建算法的细节涉及到对上述泊松方程的求解,所需数学知识已经超过了本书所涵盖的范围,对于该部分,可以参见原始论文中的详细解释 [KBH06]。