12.4. 投影变换#
前面讨论的是在二维空间和三维空间内部,如何对对象进行几何变换,而对图形学来说,一个很重要的问题就是三维物体的成像,即如何把三维对象,投影到二维平面。
12.4.1. 三维观察模型#
三维观察分两步走,第一步是求出世界坐标系下的对象在观察坐标系中的表示,第二步是从观察坐标系中将对象投影到投影平面上。
观察坐标系由三维空间中的位置 \(\mathbf{P}\)、观察平面法向量 \(\mathbf{N}\),向上向量 \(\mathbf{V}\) 决定。在观察坐标系中,\(\mathbf{N}\) 通常是 \(z\) 轴正方向,\(\mathbf{V}\) 是 \(y\) 轴正方向,\(x\) 轴方向根据左右手坐标系来决定。观察坐标系确定之后,观察对象可以先通过 §12.3 中介绍的坐标系变换从全局坐标系变换到观察坐标系下,然后在局部坐标系下进行投影。
常见的投影方法分为两种:正交投影(orthographic projection)和透视投影(perspective projection)。正交投影坐标位置沿平行线变换到观察平面上,平行投影保持对象的比例关系不变,平行线在平行投影中也是平行的。透视投影对象位置沿汇聚到观察平面后一点的直线变换到投影坐标系,透视投影不保持对象的比例关系,但真实感较好,透视投影满足近大远小的效果。
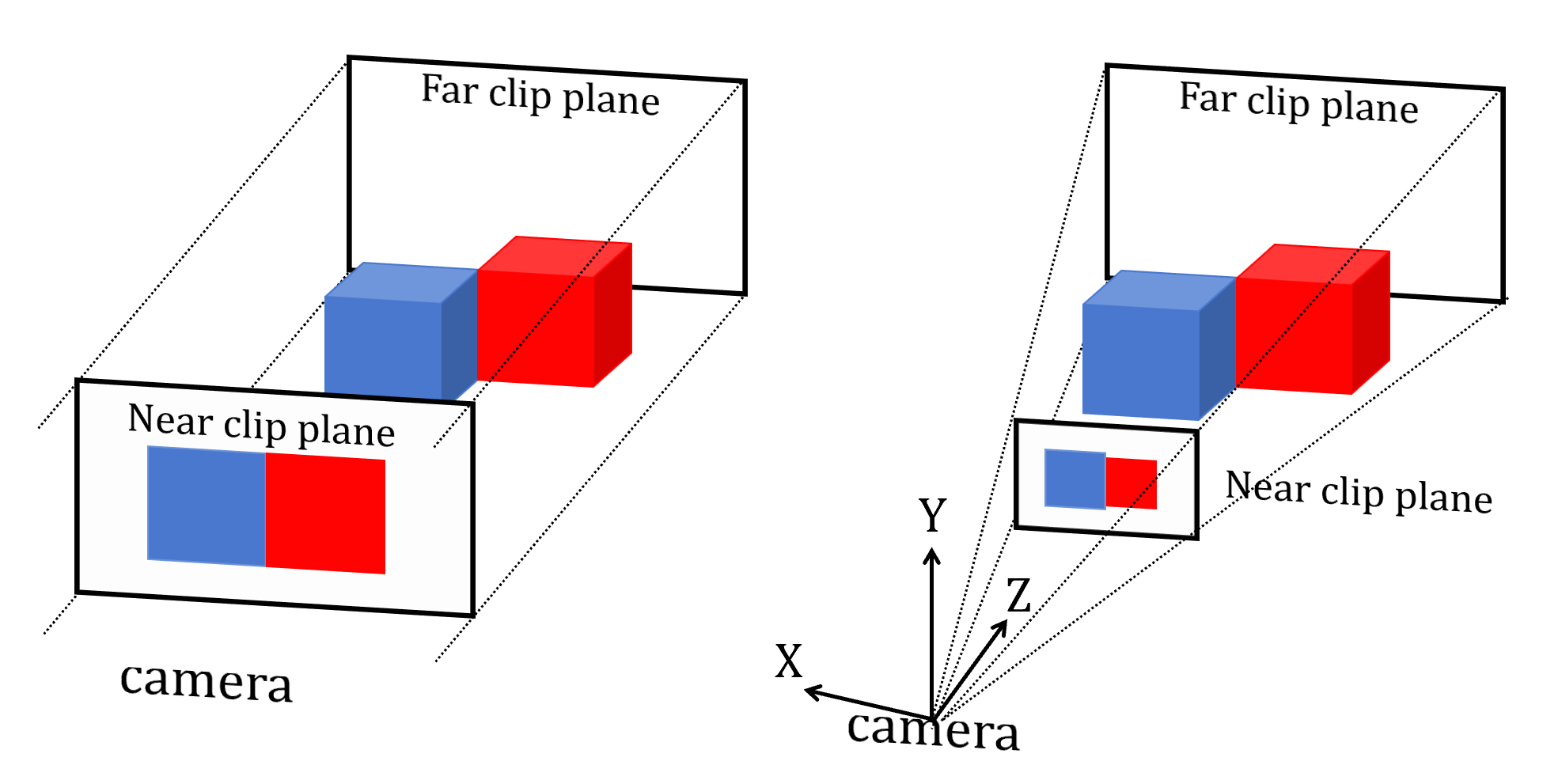
图 12.6 正交投影和透视投影示意图。#
12.4.2. 正交投影#
连接对象点与投影点的值线称为投影线,所有投影线平行的投影称为平行投影,正交投影属于平行投影的一种,投影线均与投影平面垂直,投影线不与投影平面垂直的称为斜投影。正交投影常被用来生成对象的三视图(前、侧、顶),工程和建筑测绘常用正交投影,因为可以精确绘制长度和角度,并能从图中测量出来。
通常情况下,成像平面大小是有限的,所以对应的三维观察空间也是有限的,这个空间称为正投影观察体,观察体的上下沿和两侧,由与投影平面边框垂直的平面组成,而沿投影平面法向 \(\mathbf{N}\),也是 \(z\) 轴方向的边缘,通过选取平行于投影平面的两个平面决定,这两个平面称为近裁剪平面 \(z_\mathrm{near}\) 和远裁剪平面 \(z_\mathrm{far}\)。
对于正投影来说,从观察坐标到观察平面的变换很简单,任意一点 \((x,y,z)\) 的投影点就是 \((x,y)\)。为了使观察处理独立于输出设备,图形系统通常将对象描述转换到规范化坐标系,规范化坐标系坐标范围为 \([-1,1]\)(也有一些为 \([0,1]\)),所以,\((x,y,z)\) 最后需要投影到边长为 \(2\),范围从 \((-1,-1,-1)\) 到 \((1,1,1)\) 的立方体内,设观察体在 \(x\) 和 \(y\) 上的范围分别为 \([x_\mathrm{min},x_\mathrm{max}]\) 和 \([y_\mathrm{min},y_\mathrm{max}]\),则正交投影的变换矩阵为,
12.4.3. 透视投影#
尽管正交投影容易生成,且可以保持对象的比例不变,但它的成像缺发真实感。人眼观察和相机拍摄到的图像,通常是符合透视投影的规律。透视投影下,投影线汇聚于投影中心,投影中心到投影平面的距离称为焦距 \(f\)。一般相机的成像原理是小孔成像,小孔成像会导致图片倒过来,为了方便,将投影平面放置在拍摄对象同侧。
和正交投影类似,变换需要将观察体映射到规范化坐标系。此时的观察体是棱台形状,近剪切面 \(z_\mathrm{near}\) 小,远剪切面 \(z_\mathrm{far}\) 大。考虑棱台内任意一点 \((x,y,z)\),根据相似原理,它在平面上映射的位置满足,
这里 \(x'=x\frac{f}{z}\),表达式存在一个非线性的比例因子 \(\frac1z\),并不适合用矩阵乘法表示;但在齐次坐标下,我们可以采用一个技巧,将 \(z\) 移到最后一位来表示同时除以这个比例因子:
现在,目标变成了求解矩阵中的未知数,由于 \(z\) 的变换与 \(x,y\) 无关,所以 \(A=B=0\),然后,再取两个特殊点 \(z_\mathrm{near}\) 和 \(z_\mathrm{far}\),联立方程得,
解得,\(C=z_\mathrm{near}+z_\mathrm{far}, D=-z_\mathrm{near}z_\mathrm{far}\),再应用正交矩阵的投影公式,
在图形软件中,相机参数通常被表示成视场角 \(\mathrm{fov}\),宽高比 \(\mathrm{aspect}\),近平面 \(z_\mathrm{near}\),远平面 \(z_\mathrm{far}\),上述的变换矩阵均可以用这些变量表示。