7.5. 图像缩放#
我们经常会需要调整图片的大小,并且大多数时候我们需要改变图像的长宽比,这样的任务叫做图像缩放 (image retargeting)。对于这个任务,我们最容易想到的两种办法是直接缩放和裁剪,而如图 7.26 所示,前者会导致图像内容发生形变失真,后者又会截掉很多信息。所以,为了更好地保留图片中的重要信息,我们需要一个基于图片内容的缩放算法,达到如图 7.26 右一所示的理想结果。

接缝裁剪 (seam carving) 算法[AS23] 就是一种效果非常好的基于内容的图像缩放算法。我们先来考虑图片沿着宽方向缩小的过程,在像素点大小不变的情况下,图片的缩小必然意味着信息的丢失,直接缩小图片就是删去了若干列像素,而接缝裁剪算法将“删去一列像素”改成了“删去一条像素路径”,这样一条路径又称为缝隙 (seam)。通过恰当地选择这样的缝隙,我们可以只删去一些不重要的信息,达到自然的缩放效果。
什么样的缝隙才是不重要的呢?我们可以按重要程度为每一个像素定义一个能量,那么能量路径积分最小的缝隙就是不重要的。通过前面许多算法的设计,我们应该能够认识到图片的梯度信息是十分重要的;我们可以借助前面介绍的 Sobel 算子计算出每个像素点处沿 \(x\) 和 \(y\) 方向的导数,定义能量为:
其中 \(\mathbf C(x,y)\) 为输入图像的 RGB 颜色场,图像宽 \(W\),高 \(H\)。接下来定义缝隙,一条竖直方向的缝隙是指从图片第一行到图片最后一行的八连通路径,并且图片的每一行都恰有一个像素属于该缝隙,记为 \(\mathbf{s^y}=\{s_i^y\}_{i=0}^{H-1}=\{(i,y(i))\}_{i=0}^{H-1}\);一条缝隙的能量等于它包含所有像素点的能量之和,记为 \(E(\mathbf{s^y})=\sum_{i=0}^{H-1}e(s_i^y)\)。如此一来,删掉一条缝隙意味着图片的宽度恰好减少一个像素,那么我们只需要反复找到能量最小的路径删除掉,直至图片达到目标宽度即可。
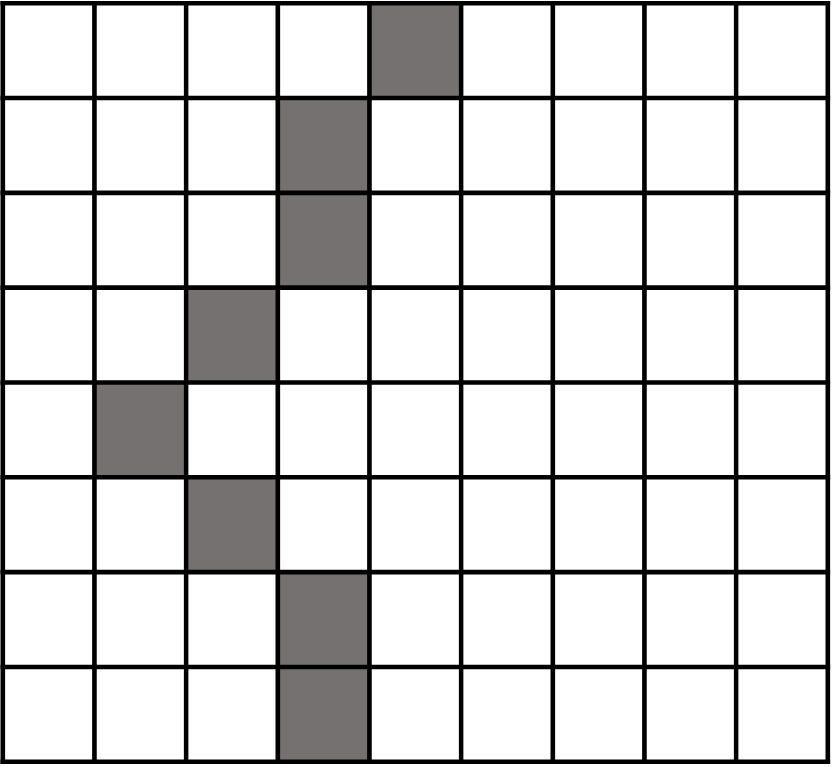
图 7.27 一条合理的竖直方向的缝隙。#
寻找最优路径可以描述为这个优化问题:
我们可以使用动态规划法求解,记 \(M(x,y)\) 表示到像素点 \((x,y)\) 的最优八连通路径的能量 (\(x\in\{0,1,\cdots,H-1\},y\in\{0,1,\cdots,W-1\}\)),那么最优的路径就对应于 \(\min_yM(H-1,y)\),而初始条件为 \(M(0,y)=e(0,y)\)。注意我们的八连通路径只能向下延伸,每个像素点的路径只可能来源于左上、上方、右上三个像素点,所以转移方程为
总结一下,用接缝裁剪算法将图像沿着宽方向缩小的过程如下:
接缝裁剪算法还能够用在图像拉伸上,每找到一条缝隙,就将缝隙上每一行的像素点与它左右相邻的像素平均后再插入到原图。但是一次只插入一条缝隙可能会导致每次插入的缝隙几乎都在同一个位置,从而出现如图 7.28 左数第二张所示的现象。解决这个问题的方法是一次性找到能量最小的 \(k\) 条缝隙,然后依次填补,得到如图 7.28 第三张所示的结果。

图 7.28 图像沿宽度方向的拉伸。从左到右依次为原图、一次插入一条缝隙的结果、一次计算的多条缝隙、一次插入多条缝隙的结果。[AS23]#