合成

4.3. 合成#

../../_images/house.png

图 4.15 使用画板绘制的简笔画#

在前面我们介绍了直线、多边形这些简单几何体的光栅化方法以及如何给它们上色，距离完成一幅像图 4.15 这样的简笔画就差将它们合成起来。观察图中的细节，我们发现在合成阶段主要有两个问题需要解决：1. 如何处理前后遮挡关系；2. 如何处理半透明的颜色。下面我们研究一下这两个问题。

4.3.1. 深度缓存#

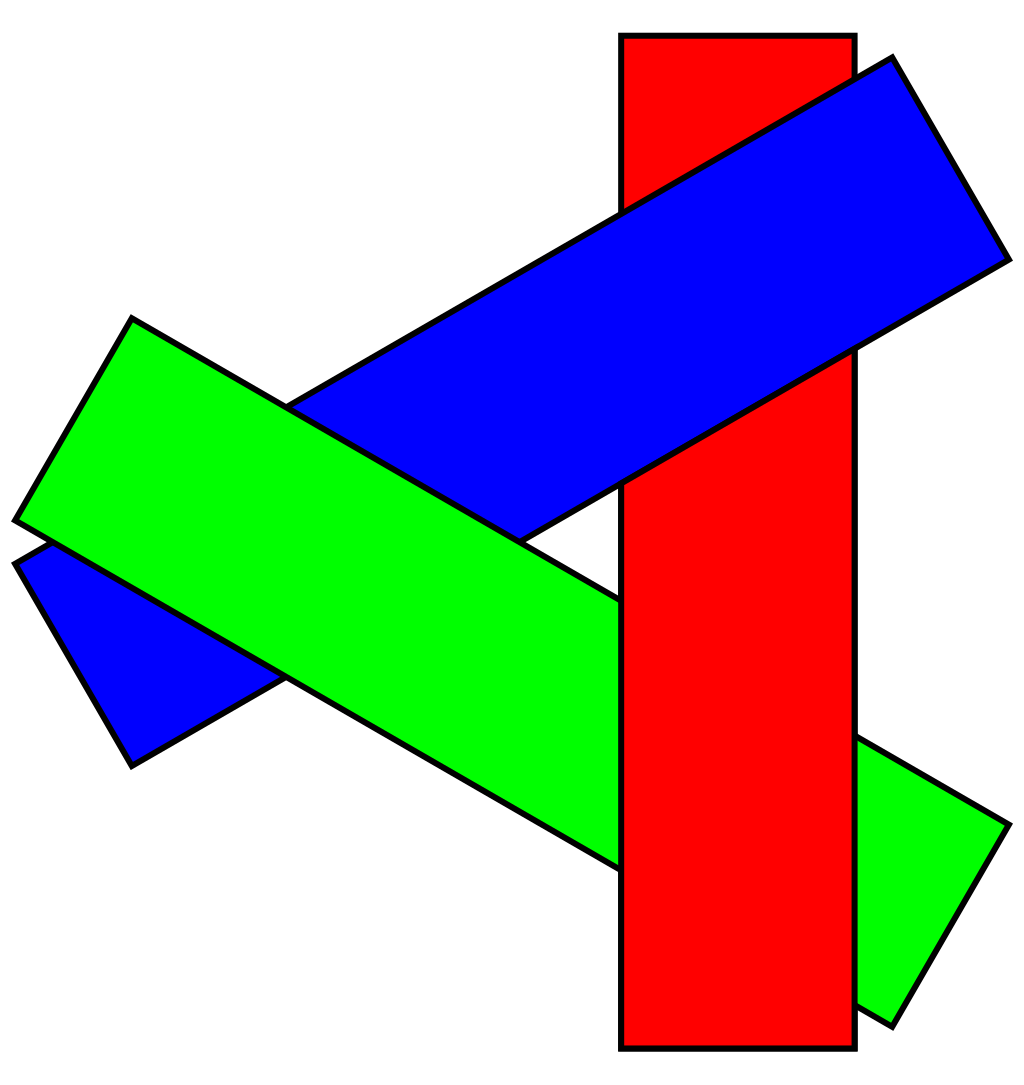
如果我们要在纸上完成一张风景画，会先绘制背景中的远山，再绘制近处的房屋，最后画最近处的人物。将这个过程改成算法，对应我们给每个形状一个额外的深度属性 \(z\)，\(z\) 越大表示离我们越远；然后对所有形状的深度进行排序，按照 \(z\) 从大到小的顺序进行绘制。这样的算法就称为画家算法（Painter’s Algorithm），如图 4.16 所示。

../../_images/painter.png

图 4.16 画家算法流程#

画家算法非常符合直觉，其主要的时间开销在于对所有形状深度进行排序，计算复杂度为 \(O(n\log n)\)。然而画家算法会在某些时候遇到问题，比如图 4.17 中的情况。在图中 R，P，Q 三个三角形没有严格的深度前后关系，P 在 R 之下，但是又在 R 之上的 Q 之上。在这种时候，我们无法定义每个形状的深度到底是多少。观察图 4.15 ，你会发现图中的树、房子、小兔子也满足这样的深度关系。究其原因在于，这种情况只能发生在三维世界中，每个物体的深度确实就不是一个固定值。

../../_images/painter1.png

图 4.17 画家算法遇到问题的情况#

为了解决这个问题，我们可以为每个像素引入一个深度值。与之前在 §2.2 中介绍的储存颜色的帧缓存的概念对应，屏幕上所有像素点的深度值构成深度缓存（depth buffer）。每个图形的深度值也不一定是固定的，在内部可以是变化的，比如通过插值得到。深度缓存记录的是当前像素的最小深度，也就是离我们最近的位置是多深。在绘制时，我们也不再需要对所有图形进行排序，而是每个像素独立检测，如果发现等待绘制的图形上的深度小于当前像素的深度，则覆盖当前像素并更新最小深度；否则表示图形被遮挡，不更新屏幕像素。算法的伪代码如代码 4.6 所示。

代码 4.6 深度缓存算法#
1depth_buffer = initialize_depth_buffer()
2
3for shape in shapes:
4  for pixel in shape:
5    depth = get_shape_depth(pixel)
6    if depth < depth_buffer[pixel]:
7      draw(shape, pixel)
8      depth_buffer[pixel] = depth

深度缓存算法还带来了计算复杂度上的好处，我们不再需要对所有形状进行排序，而只需要维护深度最浅的像素，这是一种空间换时间的做法。在后面的 §14 章节，我们还能看到深度缓存方法在三维渲染的应用。

4.3.2. 半透明#

如果存在半透明的物体，我们最终看到的颜色应该是上下层颜色的混合，就像图 4.15 中的云朵。我们用不透明度（opacity） 来表达物体透明的程度，一般用 \(\alpha\) 表示，因此也可以直接叫 alpha 值。\(\alpha=1\) 表示完全不透明，\(\alpha=0\) 表示完全透明。也可以用相反的透明度（transparency） 来表示，等于 \(1-\alpha\)。我们可以为每个像素指定不透明度，因此可以把不透明度作为颜色的第四维放到一起，称为 RGBA 色彩空间，其中最后一个 A 就表示 alpha 通道。

现在我们考虑在背景颜色 \(c_d\) 上叠加一个半透明颜色 \(c_s\)，对应的不透明度是 \(\alpha\)，最终的颜色 \(c_r\) 应该由下面的公式给出：

(4.4)#\[ c_r = (1-\alpha) c_d + \alpha c_s \]

这也很好理解，\(1-\alpha\) 描述了有多少光能从下面透过来，\(\alpha\) 描述了不透明物体本身能显示多少颜色。接下来考虑一个稍微复杂的情况，背景颜色是 \(c_0\)，先叠加不透明度为 \(\alpha_1\) 的颜色 \(c_1\)，然后是不透明度为 \(\alpha_2\) 的颜色 \(c_2\)，最后的颜色应该是什么。我们从后到前计算：

(4.5)#\[\begin{split} \begin{aligned} c_{01} &= (1-\alpha_1) c_0 + \alpha_1 c_1 \\ c_{012} &= (1-\alpha_2) c_{01} + \alpha_2 c_2 = (1-\alpha_1)(1-\alpha_2) c_0 + \alpha_1(1-\alpha_2) c_1 + \alpha_2 c_2 \end{aligned} \end{split}\]

这时如果我们交换 \((c_1, \alpha_1)\) 和 \((c_2, \alpha_2)\) 的顺序，代入公式 (4.5) 中，可以发现最终颜色 \(c_{021} \neq c_{012}\)。这表示半透明的合成是和顺序有关系的。因此，对于半透明材料我们往往要使用不同于不透明物体的算法：使用画家算法先排序后绘制，而不能直接使用深度缓存算法。

../../_images/transparent.png

图 4.18 相同的两个半透明色块绘制顺序不同重叠部分颜色也不同#

从公式 (4.5) 中，我们也能导出两个半透明颜色之间的混合公式。假设 \((c_1, \alpha_1)\) 在下，\((c_2, \alpha_2)\) 在上，我们希望合成出一个等价的半透明颜色 \((c_{12}, \alpha_{12})\)，使得公式 (4.5) 中的 \(c_{012}\) 等于 \(c_0\) 与 \((c_{12}, \alpha_{12})\) 直接合成：\(c_{012} = (1-\alpha_{12}) c_0 + \alpha_{12} c_{12}\)。对比两个公式我们可以得到合成关系：

(4.6)#\[\begin{split} \begin{aligned} \alpha_{12} &= 1 - (1-\alpha_1)(1-\alpha_2) = \alpha_1 + \alpha_2 - \alpha_1 \alpha_2 \\ c_{12} &= \frac{\alpha_1(1-\alpha_2)}{\alpha_{12}} c_1 + \frac{\alpha_2}{\alpha_{12}} c_2 \end{aligned} \end{split}\]

公式 (4.6) 还有一点边界条件需要处理，当 \(\alpha_{12}=0\) 时，意味着 \(\alpha_1=0\) 并且 \(\alpha_2=0\)，此时两个物体都是全透明的，\(c_{12}\) 可以给任意值。