23.4. 本章小结#
23.4.1. 习题#
光滑粒子流体动力学方法在进行模拟时经常需要遍历一个粒子的所有邻居（即核函数非零域内的所有粒子），对此在 §23.2 中我们的处理方式是检查模拟域内所有的粒子。利用哈希网格（Hash grid）可以加速这个过程：将整个模拟区域划分成边长为核半径 \(h\) 的网格，并对每个格子维护一个链表，链表中存储处于该格子内全部粒子的索引；此外，维护每个粒子所属的格子。请利用这些数据结构，简要写出遍历一个粒子所有邻居的步骤。
在光滑粒子流体动力学中我们常使用的核函数 \(W_\mathrm{cubic}\) 形式如式 (23.4) 所示，定义另一个核函数如下：
\[\begin{split} W_1(r,h)= \begin{cases} \frac 1r&0<r\le h\\ 0&\text{otherwise} \end{cases}， \end{split}\]请分别计算 \(\lim_{r\to 0^+}W_\mathrm{cubic}(r,h)\)、\(\lim_{r\to 0^+}W_1(r,h)\)，以及 \(\lim_{r\to h^-}W_\mathrm{cubic}(r,h)\)、\(\lim_{r\to h^+}W_\mathrm{cubic}(r,h)\)、\(\lim_{r\to h^-}W_1(r,h)\)、\(\lim_{r\to h^+}W_1(r,h)\)。你觉得哪个核函数更好？请从这些计算结果出发，给出两个原因。光滑粒子流体动力学方法非常适合自由表面流体的模拟，如果我们可以计算出流体的表面法向，就能进一步通过法向计算表面张力，从而模拟出诸如水滴、水膜等表面张力现象。
为计算表面法向，我们可以回顾一下压强场是如何计算的：
\[ p(\boldsymbol x)=\sum_{i}p_i\frac{m_i}{\rho_i}W(\|\boldsymbol x-\boldsymbol x_i\|)， \]已知每个粒子 \(i\) 的密度 \(\rho_i\) 和压强 \(p_i\)，则粒子体积为 \(V_i=\frac{m_i}{\rho_i}\)；那么对于空间中任意一点 \(\boldsymbol x\)，该点处的压强就是附近粒子的压强按核函数乘以粒子体积为权重的加权和。这样就可以把仅仅定义在粒子上的压强 \(p_i\) 拓展到全空间上都有定义的压强场 \(p(\boldsymbol x)\)，并且由于 \(W(r)\) 是光滑的，得到的 \(p(\boldsymbol x)\) 也是光滑的（即无穷阶可导）。现在我们希望用类似方法定义一个新的标量场 \(c(\boldsymbol x)\)，当 \(\boldsymbol x\) 处于流体内部且远离表面时 \(c(\boldsymbol x)\) 近似为常数，当 \(\boldsymbol x\) 处于流体外部且远离表面时 \(c(\boldsymbol x)=0\)。那么借助 \(c(\boldsymbol x)\) 的光滑性，可以立即得出 \(c(\boldsymbol x)\) 在流体表面附近的梯度方向由流体的外部指向内部，且近乎垂直于表面，从而可以得到表面法向；同时在远离表面的部分 \(c(\boldsymbol x)\) 的梯度接近于零，这样就可以辨别出那些粒子离表面很近，进而计算这些粒子上的梯度得到表面法向。已知粒子的位置 \(\boldsymbol x_i\)、密度 \(\rho_i\) 和质量 \(m_i\)，定义在粒子上的常量 \(c_i=1\)，请写出 \(c(\boldsymbol x)\) 和 \(\nabla c(\boldsymbol x)\) 的表达式（此处的梯度应使用式 (23.7) 的形式）。
请写出使用标记网格计算三维情形下速度散度 \((\nabla\cdot\boldsymbol u)_{i,j,k}\)，压强梯度 \(\left(\frac{\partial p}{\partial x}\right)_{i+\frac 12,j,k}\)、\(\left(\frac{\partial p}{\partial y}\right)_{i,j+\frac 12,k}\)、\(\left(\frac{\partial p}{\partial z}\right)_{i,j,k+\frac 12}\) 的表达式。
考虑一个三维标记网格中刚刚对流过的有符号距离场 \(\phi_{i+\frac 12,j+\frac 12,k+\frac 12}^*\)，在对其重新计算的过程中遍历到了格子顶点 \(\left(i+\frac 12,j+\frac 12,k+\frac 12\right)\)，令 \(\phi_0\)、\(\phi_1\)、\(\phi_2\) 分别对应于 \(x\) 轴、\(y\) 轴、\(z\) 轴方向上邻居 \(\phi^*\) 的较小值，请写出计算 \(\phi^{n+1}_{i+\frac 12,j+\frac 12,k+\frac 12}\) 的步骤。
请画出图 23.8 中初始状态下的标记网格在外插速度场后得到的 \(\hat{\boldsymbol u}^n\) 的结果，再进行对流过程 \(\phi^*\gets\mathrm{Advect}(\hat{\boldsymbol u}^n,t_{n+1}-t_n,\phi^n)\) 和 \(\boldsymbol u^*\gets\mathrm{Advect}(\hat{\boldsymbol u}^n,t_{n+1}-t_n,\boldsymbol u^n)\) 并标出 \(\phi^*\) 与 \(\boldsymbol u^*\) 的结果。
考虑一个水格子 \((i,j)\)，它的左边是固体，上边是空气，右边、下边均是水，如图 23.9 所示。请写出这个格子对应的压强方程。
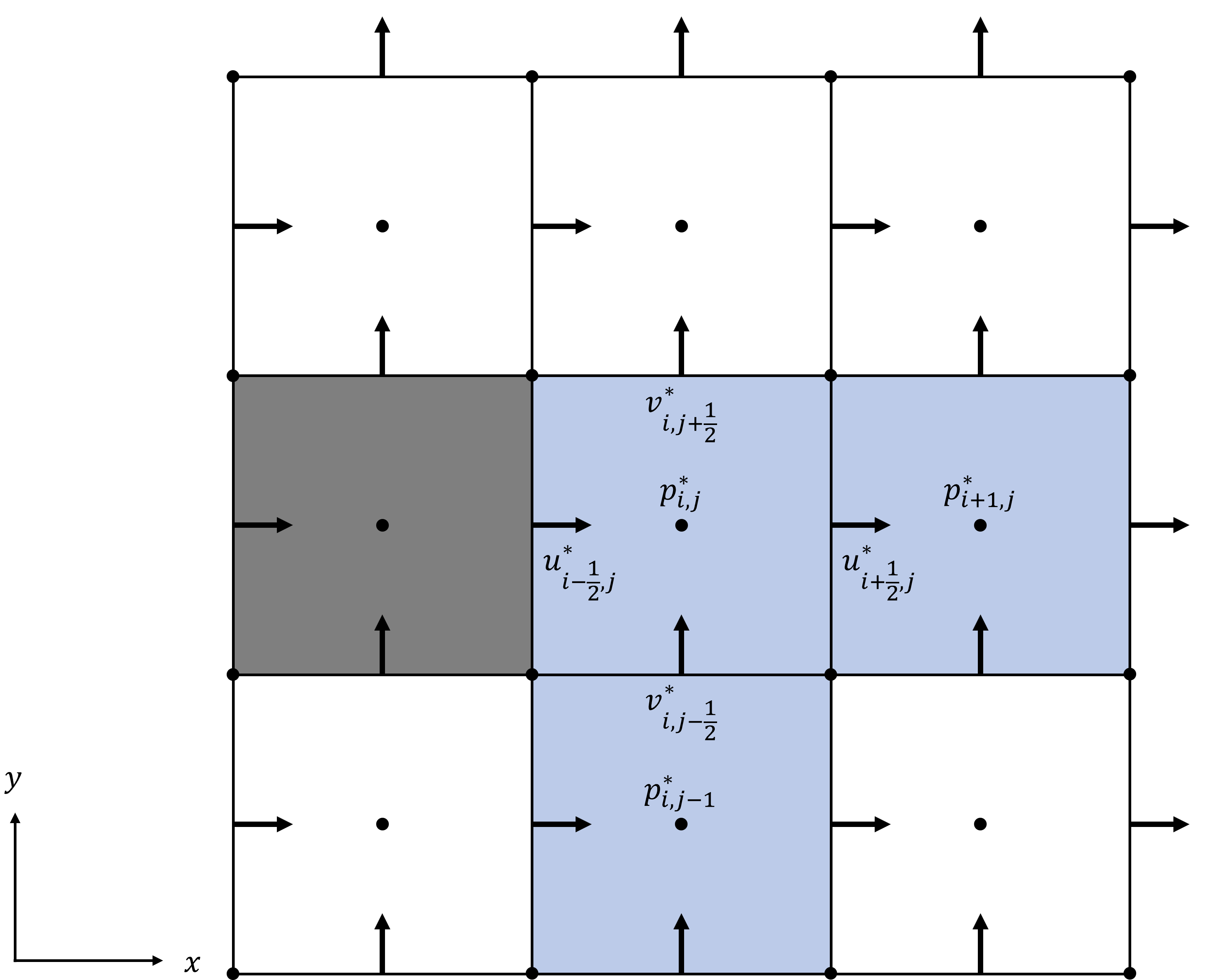
图 23.9 第 7 题图#
23.4.2. 参考文献#
Jan Bender and Dan Koschier. Divergence-free sph for incompressible and viscous fluids. IEEE Transactions on Visualization and Computer Graphics, 23(3):1193–1206, 2017. doi:10.1109/TVCG.2016.2578335.
Markus Ihmsen, Jens Cornelis, Barbara Solenthaler, Christopher Horvath, and Matthias Teschner. Implicit incompressible sph. IEEE Transactions on Visualization and Computer Graphics, 20(3):426–435, 2014. doi:10.1109/TVCG.2013.105.
B. Solenthaler and R. Pajarola. Predictive-corrective incompressible sph. ACM Trans. Graph., July 2009. URL: https://doi.org/10.1145/1531326.1531346, doi:10.1145/1531326.1531346.