信号理论

5.1. 信号理论#

为了了解走样的本质，我们考虑一维情况的图形学，也即只考虑对一维的连续信号进行离散采样。二维光栅化可以看成是两个方向的一维采样。如图 5.4 所示，我们固定采样的频率（像素密度），逐渐增加连续信号的频率，观察离散化之后的信号形状：\(f_1(x)\) 和 \(f_2(x)\) 的离散结果可以正确反映连续信号的形状，但是频率增加到 \(f_3(x)\) 开始有一些失真，到 \(f_4(x)\) 和 \(f_5(x)\) 离散信号和连续信号就完全不一样了。观察 \(f_5(x)\) 的结果，我们可以发现离散信号是以一个不同于连续信号的频率在振荡，也即可以理解为出现了摩尔纹。

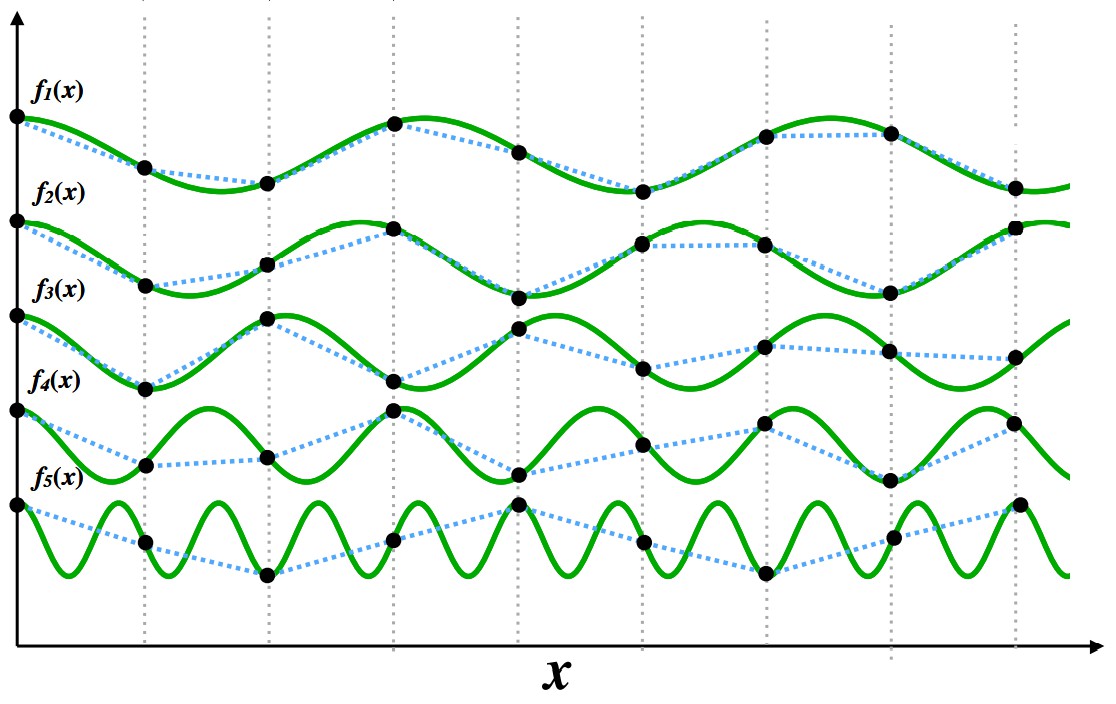
../../_images/cos.jpg

图 5.4 以相同的采样频率采样频率不同的余弦信号：竖向灰色虚线代表采样位置，灰色虚线与信号的交点代表信号的采样点#

这个基础的余弦函数的例子展示了走样是如何发生的，想要将结论拓展到一般的函数，我们需要用到傅里叶变换。

关于傅里叶变换和采样的理解可以参考 GAMES001 中的傅里叶变换与球谐函数部分。

5.1.1. 傅里叶变换#

假设我们有一个周期为 \(T\) （频率为 \(\frac{1}{T}\)）的周期函数，比如图 5.5 中的方波函数，我们可以使用一系列的频率为 \(\frac{1}{T}\) 整倍数的正弦和余弦函数（统称为简谐函数）加和近似，这个过程称为周期函数的傅里叶展开（Fourier Expansion）。

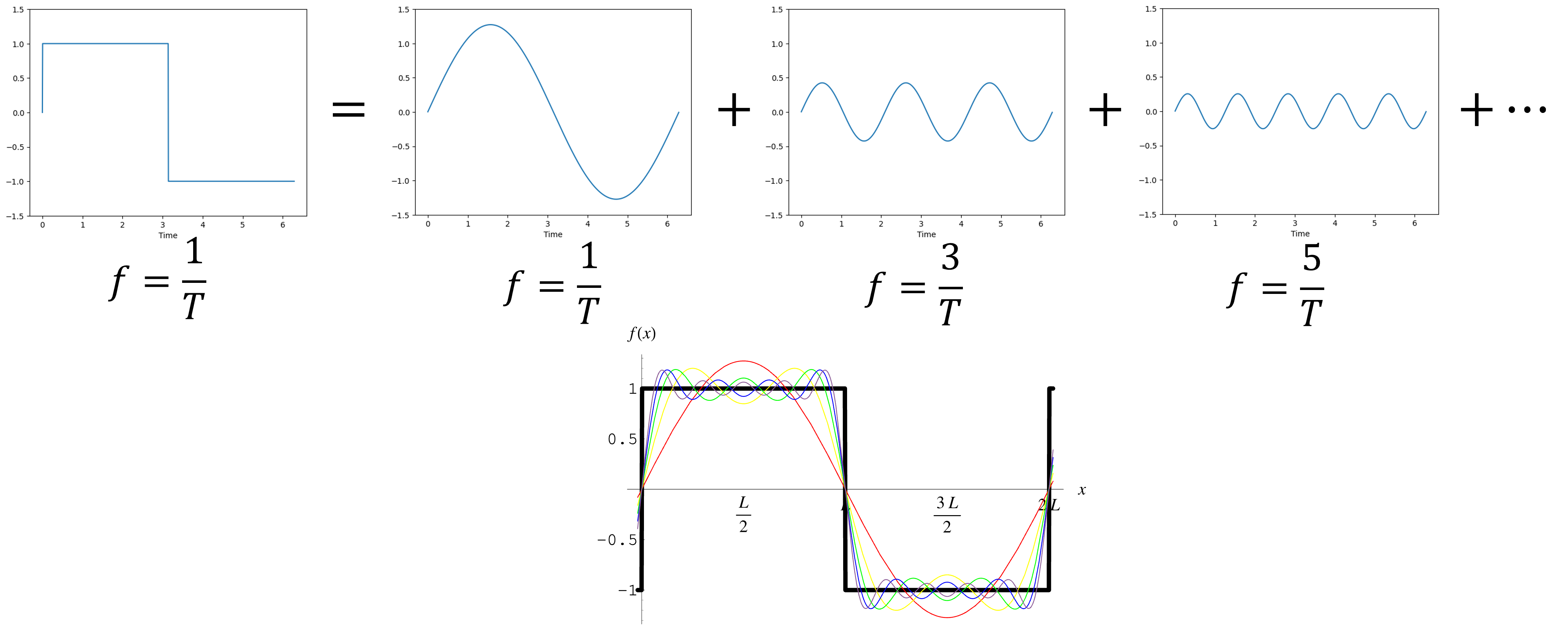
../../_images/square-wave.png

图 5.5 方波函数的傅里叶展开#

这个展开揭示了周期信号其实可以当成是简谐信号的叠加，只不过里面包含了很多不同频率和振幅的简谐信号。我们使用的简谐信号越多，就能越准确地还原原信号。用公式写出来，对于一个周期为 \(T\) 的周期函数，我们有：

(5.1)#\[\begin{split} \begin{aligned} f(x) &= \frac{a_0}{2} + \sum_{n=1}^{\infty} \left( a_n \cos(\frac{2n\pi}{T} x) + b_n \sin(\frac{2n\pi}{T} x) \right) \\ a_n &= \frac{2}{T} \int_{-T/2}^{T/2} f(x) \cos(\frac{2n\pi}{T} x) \, dx\\ b_n &= \frac{2}{T} \int_{-T/2}^{T/2} f(x) \sin(\frac{2n\pi}{T} x) \, dx \end{aligned} \end{split}\]

如果是一般的非周期的函数 \(f(x)\)，我们还有类似的结论吗？注意到非周期函数其实可以看成周期 \(T\) 趋向于正无穷的周期函数，我们说频率为 \(\frac{1}{T}\) 整倍数的简谐函数也就包括了所有频率的简谐函数，对应的公式 (5.1) 中的求和也就变成了积分。所以一个非周期函数同样存在傅里叶展开，不过改称为傅里叶变换（Fourier transform），由下面的公式给出：

(5.2)#\[\begin{split} \begin{aligned} f(x) &= \int_{-\infty}^{\infty} F(\omega) e^{2\pi i \omega x} d\omega = \int_{-\infty}^{\infty} F(\omega) (\cos(2\omega\pi x) + i\sin(2\omega\pi x)) d\omega\\ F(\omega) & = \int_{-\infty}^{\infty} f(x) e^{-2\pi i \omega x} dx = \int_{-\infty}^{\infty} f(x) (\cos(2\omega\pi x) - i\sin(2\omega\pi x)) dx \end{aligned} \end{split}\]

公式 (5.2) 与公式 (5.1) 看起来非常不同，但其实有直接的对应关系：

  • (5.2) 中的 \(\omega\) 对应 (5.1) 中的 \(\frac{n}{T}\)，表示频率

  • (5.2) 中的 \(F(\omega)\) 是一个复函数，实部和虚部分别对应 (5.1) 中的余弦函数的振幅 \(a_n\) 和正弦函数的振幅 \(b_n\)

  • \(e^{i\theta}=\cos \theta + i\sin \theta\) 是欧拉公式，为了可以方便表示简谐函数

  • (5.2) 中的第一个积分式对应 (5.1) 中的求和

  • (5.2) 中的第二个积分式对应 (5.1) 中 \(a_n\) 和 \(b_n\) 的具体形式

到这里我们就明白了傅里叶变换到底说的是什么意思。对于一个函数 \(f(t)\)，我们能对应找到一个复函数 \(F(\omega)\)，它们表示的是同一个东西，并可以使用公式 (5.2) 这样一个对称的变换相互转换。\(F(\omega)\) 提供了理解函数的另一个视角，称为频谱（spectrum），对应 \(\omega\) 所在的空间就是频域空间（frequency domain）。

5.1.2. 频谱#

我们通过一个例子来看频谱的作用。在图 5.6 中，我们展示了对一张图片做傅里叶变换。图片可以看成一个二维函数 \(f(x,y)\)，对应频域也是一个二维空间 \((\omega_x,\omega_y)\)，对应的傅里叶变换形式与公式 (5.2) 类似，只不过都要换成二重积分。我们把频谱函数 \(F(\omega_x,\omega_y)\) 可视化出来，画到图 5.6 的第二行。

../../_images/lena.png

图 5.6 图片的频谱与低通滤波#

从图 5.6 可以看到，频谱的中心（低频部分）非常亮，表示对应简谐函数的振幅很大，越到边缘（高频部分）振幅越小，这与我们在方波函数图 5.5 中的观察是一致的。如果我们截断频谱中的高频部分，比如像图 5.6 中一样只保留一个小方块内部的频谱，而把之外的都置零，可以发现变换回去的图片变模糊了，但是依然有整体的形状。因此我们可以得出结论，图像的大部分形状信息都保存在了频谱的低频部分，高频部分只是一些细节。通过这种方式，我们可以实现对图像的压缩，这是现在图像、视频压缩的主流算法。

5.1.3. 采样理论#

使用傅里叶变换，我们可以从频域的角度理解采样的过程。我们忽略具体的推导，只给出最终结论：对一个连续函数 \(f(x)\)，我们以 \(f_s\) 的频率进行采样，最终得到的离散函数的频谱，是把 \(f(x)\) 的频谱 \(F(\omega)\) 在每隔 \(f_s\) 的位置复制一份，也称为对 \(F(\omega)\) 以 \(f_s\) 为周期进行周期延拓（periodic extension），如图 5.7 所示。

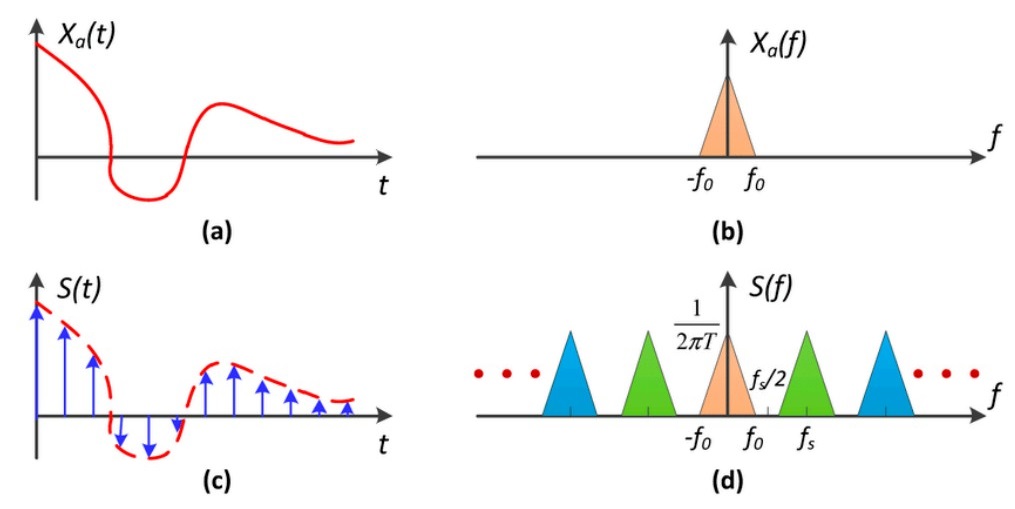
../../_images/freq_sample1.jpg

图 5.7 连续信号及其采样信号的时域图和频域示意图：(a) 为连续信号，(b) 为对应的频谱，(c) 表示对连续信号进行频率为\(f_s\)的离散采样，也就是每隔\(1/f_s\)采样一个值，(d) 表示采样得到的离散信号的频谱，是将连续信号的频谱按周期 \(f_s\) 进行周期延拓#

证明结论的核心需要使用傅里叶变换的卷积定理[1]，这里我们就不展开了。尽管最终的结论比较反直觉，但是可以发现采样结果的频谱确实同时包含了原信号的频谱成分 \(F(\omega)\) 和采样频率 \(f_s\) 的成分。如果采样频率趋向于无穷，那么周期延拓之间的距离就会趋向无穷远，这时采样的频谱就是原信号的频谱。假设原信号存在截至频率 \(f_0\)，也就是频谱在频率 \(f_0\) 以上都是 0，那么只要 \(f_s > 2 f_0\)，我们总是可以通过只保留 \([-f_0, f_0]\) 部分频谱的方式从采样的结果中恢复出原信号。反之如何采样频率比较小，那周期延拓的各个部分之间就可能发生重叠，如图 5.8 所示。

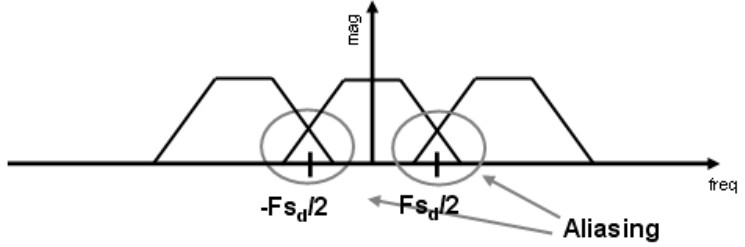
../../_images/sample_sparse.jpg

图 5.8 较低的采样频率产生频谱交叠#

发生混叠意味着原信号频谱的形状遭到了破坏。这时我们再截断 \([-f_0, f_0]\) 中的部分，里面包含了错误的频率信息，就无法再恢复出原信号了。换句话说，此时走样现象就发生了。因此，想要能完美恢复出原信号，我们必须要让采样频率至少是原信号截止频率的两倍：

(5.3)#\[ f_s > 2 f_0 \]

这个结论就是著名的奈奎斯特-香农采样定理（Nyquist-Shannon sampling theorm）。到这里，我们理解了走样现象是如何发生的，并给出了数学判断标准：一切的原因在于采样频率的不足。那么接下来的问题就是：如何在采样频率有限的情况下减轻或避免走样的发生？