6.2. 样条曲线#
样条曲线(spline curve) 是定义非常广泛,也是最常用的曲线类型。事实上,只要是使用分段多项式表达的曲线,并且在连接处满足一定的连续性,我们就可以称这条曲线为样条曲线。样条的名称来源于早期的船舶和飞机制造工业中的一种技术:通过将细木条 (称为“样条”) 穿过布置在大型设计阁楼地板上的点来构建飞机模板,如图 6.6 所示。如果我们使用分段的多项式近似整个细木条,得到的曲线就称为样条插值曲线。后来样条曲线被赋予了更广泛的定义,不需要经过这些控制点也可以被称为样条曲线。
6.2.1. 插值样条#
给出点列 \(\{\mathbf P_0,\,\mathbf P_1,\,\dots,\,\mathbf P_m\}\),其中每个点的坐标为 \(\mathbf P_i = (x_i,\,y_i)\)。我们的任务是在每个区间内定义一个多项式,使其经过每个点并保持一定连续性。常见的选择是三次样条(cubic spline):假设在每一段 \((\mathbf P_i, \mathbf P_{i+1})\) 之间我们都定义一个参数 \(t\in [0, 1]\),然后假设 \(x=f_i(t)=a_i t^3 + b_i t^2 + c_i t + d_i\),\(y=g_i(t)=e_i t^3 + f_i t^2 + g_i t + h_i\),一共 8 个参数需要确定。由于 \(x\) 和 \(y\) 可以单独考虑,我们下面的推导只针对 \(x\) 分量,\(y\) 分量同理。
针对 \(x\) 分量我们一共需要确定 \(4m\) 个参数,对应要列出 \(4m\) 个方程。首先,每个区间应该经过左右两个端点,这样有 \(2m\) 个方程:
在每个点上我们要求左右连续:对于 \(\mathbf{P}_i\),左侧区间代入 \(t=1\) 的一阶导数和二阶导数应该和右侧 \(t=0\) 的一阶导数和二阶导数相等。这样的方程我们一共可以列 \(2(m-1)\) 个:
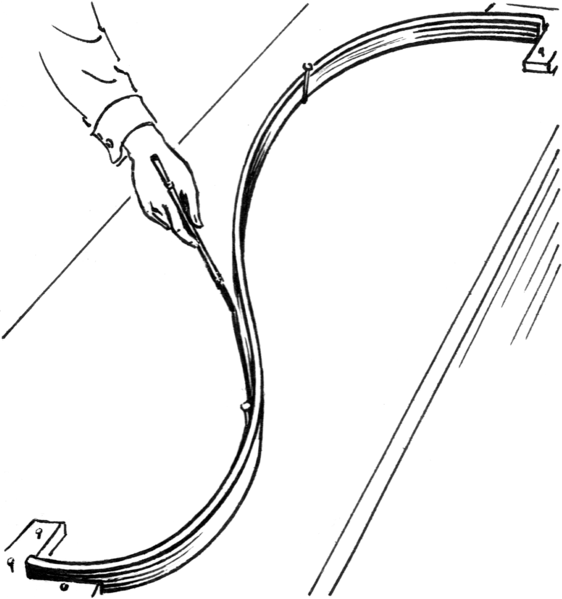
这些方程加起来一共有 \(4m - 2\) 个,还差 2 个方程。这两个方程可以自行指定,比如我们可以规定两个端点处的二阶导数为 0:\(f''_0(0)=0\),\(f''_{m}(1)=0\),这种特例称为自然边界条件。这样我们一共列出了 \(4m\) 个方程,对应 \(4m\) 个未知数,只需要求解 \(4m\times 4m\) 的线性方程组就能得到所有参数。图 6.7 给出了一个示例结果。
从定义中我们可以发现,三次样条支持 \(C^2\) 的连续性,并且是插值曲线。但是相对的,我们需要解方程确定每一段的参数,如果我们移动了某一个控制点就需要重新求解整个曲线。并且,由于我们要求解线性方程,一个控制点的移动会影响整个曲线非常远地方的形状。这种特性称为非局部性。
为了改进三次样条的缺点,有一种非常类似的样条曲线,称为三次厄米样条(cubic Hermite spline)。三次厄米样条依然使用分段的三次多项式表示曲线,与三次样条不同的地方在于,三次厄米样条不要求二阶导数的连续。作为交换,我们可以指定每个顶点上的一阶导数的值。假设我们指定点 \(\mathbf{P}_i\) 上的导数为 \((p_i, q_i)\),那么对于 \((\mathbf P_i, \mathbf P_{i+1})\) 之间的三次函数,我们可以列出下面的边界条件:
这是 \(x\) 分量的方程,\(y\) 分量的方程同理。这四个方程刚好对应 4 个未知数 \((a_i, b_i, c_i, d_i)\),我们可以直接给出最后解出的三次函数形式:
公式 (6.13) 经过了重排,但是你可以发现它依然是一个三次多项式。事实上,公式 (6.13) 中标记出的四个多项式是有名字的,称为厄米基函数(Hermite basis functions)[3],如图 6.8 所示。
这四个基函数满足相应的特性,比如对于 \(h_{00}\) 而言,有 \(h_{00}(0)=1\),\(h_{00}(1)=0\),\(h'_{00}(0)=0\),\(h'_{00}(1)=0\)。当我们将这些特性代入公式 (6.13) 中时,就会发现它自动满足边界条件。当我们把这样一段一段的曲线拼凑起来时,就可以保证整个曲线的一阶导数是连续的,但是二阶导数不一定,因此三次厄米样条满足 \(C^1\) 光滑。
三次厄米样条曲线每个顶点上的导数可以由用户指定,也可以通过控制点计算,比如著名的 Catmull-Rom 样条(由图形学大师 Edwin Catmull 和 Raphael Rom 提出)使用的计算方法就是 \(p_i = \frac{1}{2}(x_{i+1}-x_{i-1})\)[3]。通过这种方式我们就只需要给出控制点的位置就能得到一条 \(C^1\) 光滑的插值曲线。三次厄米样条曲线与三次样条曲线相比,最大的好处在于不需要解方程来确定参数,并且具有局部性:我们只需要区间两端的位置和导数就能唯一确定区间内部曲线的形状,与其他控制点的位置无关。三次厄米样条曲线使用非常广泛,比如 PowerPoint 软件中提供的曲线工具就是三阶厄米样条曲线,用户可以自由编辑每个控制点的位置和对应的切线。
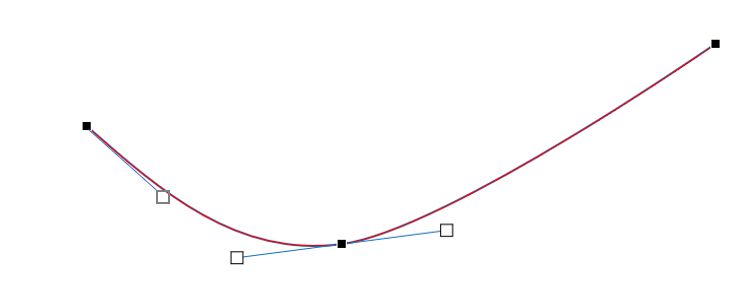
图 6.9 PowerPoint 软件中使用的是三阶厄米样条曲线#
6.2.2. B样条#
B 样条(basis spline,B-spline) 是另外一种常用的样条曲线,与三次厄米样条相比,B 样条不是插值曲线,同样具有局部性,并且光滑性更好。选定参数区间 \([a,b]\) 内一列非减的数列,满足:\(a=t_0\le t_1\le \dots\le t_m=b\),这 \(m+1\) 个数将参数区间划分成 \(m\) 段,被称为节点(knots),由这 \(m+1\) 个节点组成的集合被称为节点向量(knot vector)。
B 样条的核心是基函数(basis functions)。给定控制点点列 \(\{\mathbf P_0,\,\mathbf P_1,\,\dots,\,\mathbf P_m\}\),\(n\) 次 B 样条曲线可以表达为:
其中 \(N_{i,n}(t)\) 是节点 \(i\) 对应的基函数,是一个关于 \(t\) 的 \(n\) 阶多项式,你可以类比公式 (6.13) 中的厄米基函数,以及公式 (6.8) 中的线性基函数。B 样条独特的地方在于它的基函数是递归定义的。记节点 \(i\) 上的 \(p\) 次 B 样条基为 \(N_{i,p}(t),\,0\le i\le m,\,0\le p\le n\),它们是一组根据 Cox–de Boor 递归定义的函数:
并且满足性质:
我们在图 6.11 中画出来前几阶的 B 样条基函数。从图中和公式定义中我们能发现 B 样条基函数的几个特征:
\(N_{i,p}(t)\) 是 \(p\) 阶的分段多项式,并且在连接处保持了 \(C^{p-1}\) 的连续性,因此使用 \(N_{i,p}(t)\) 作为基函数的 B 样条可以保证 \(C^{p-1}\) 的光滑性
\(N_{i,p}(t)\) 不能保证在节点 \(i\) 上取 1,在其他节点取 0,因此不满足插值性
\(N_{i,p}(t)\) 会影响到附近连续 \(p+1\) 个区间内的值,因此 \(p\) 越大基函数影响的范围越大,局部性就越差
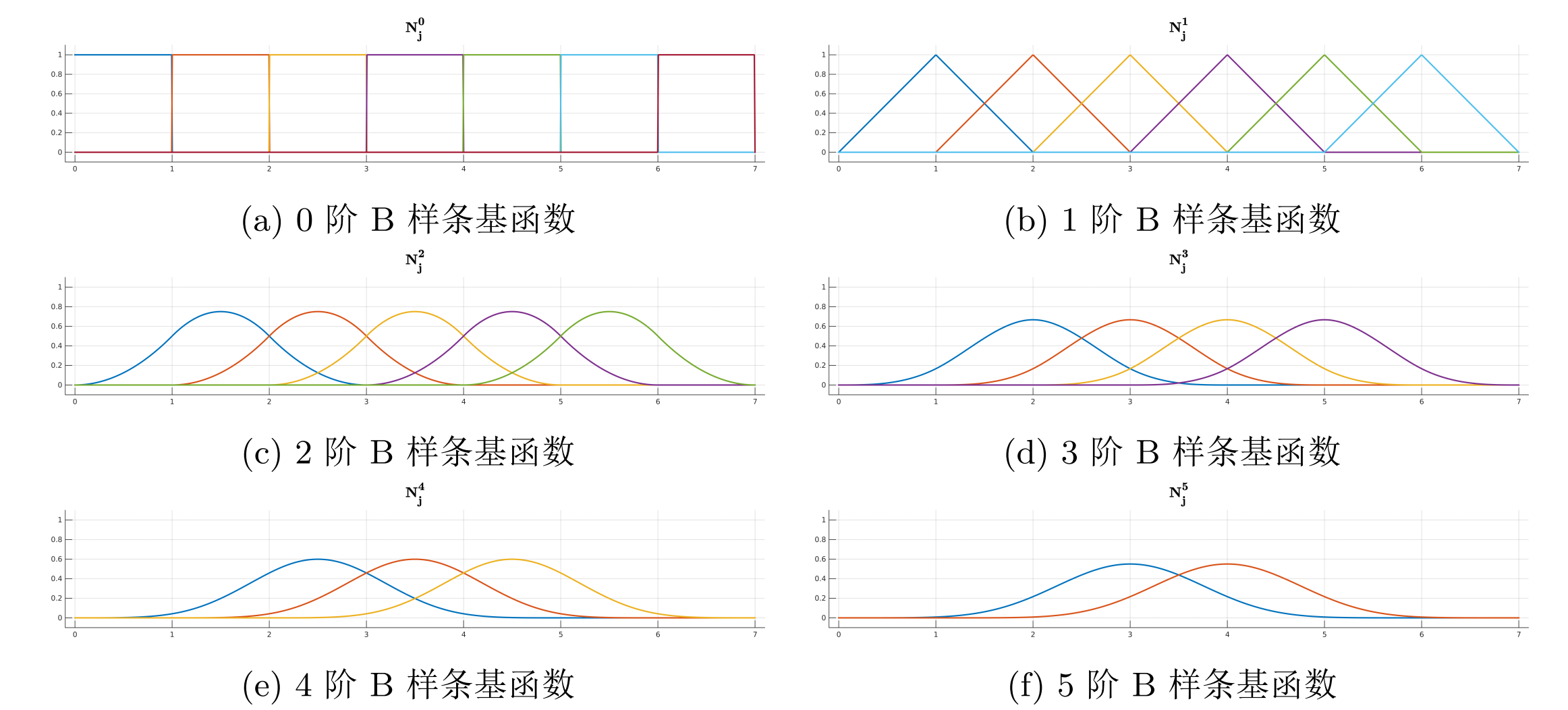
图 6.11 B 样条基函数#
B 样条的一个很大优势在于它的灵活性。比如我们可以在每一段选择不同阶数的基函数来满足不同的连续性的要求。我们还可以选择重复节点:\(t_i=t_{i+1}=\cdots=t_{i_k-1}\) 表示它是一个重复度为 \(k\) 的多重节点。重复节点内部相当于有无穷短的曲线,因此我们可以在保证整个曲线其他部分连续性的情况下在重复节点上降低连续性,比如构造出尖锐的转弯。
6.2.3. NURBS 曲线#
非均匀有理 B 样条(non-uniform rational B-splines,NURBS)是对 B 样条的一个重要扩展。在计算机辅助设计、计算机辅助制造、计算机图形学等领域中,NURBS有着十分重要的应用,为曲线、曲面设计提供了较高的灵活度。“非均匀”指的是B样条的节点在参数区间内不等距分布,“有理”指的是B样条对每个控制点也额外施加了一个权值 \(w_i\),当权值均等于1时,NURBS曲线就退化成了普通的b样条曲线。NURBS 曲线的定义为:
NURBS 曲线解决了 B 样条曲线一个很大的问题:如何表示圆锥曲线?B 样条曲线不能直接表示圆弧,因为本质上其是多项式。但是 NURBS 曲线可以通过选择合适的权重和基函数来表示一个完美的圆周,如图 6.12 所示,这里我们就不深入细节了。