光滑粒子流体

23.2. 光滑粒子流体#

在计算机中用拉格朗日视角描述流体的方式就是将流体表示成一系列粒子，每个粒子代表一个流体微团，即是物质本身，因此随体导数就是粒子所携带物理量关于时间的导数。基于这个思想的流体模拟方法统称为粒子法，这类方法中应用最普遍的称为光滑粒子流体动力学（smoothed particles hydrodynamics，SPH），本节我们将带领大家了解这个方法最基础的实现方式。

23.2.1. 空间离散化#

../../_images/animation-fluids-sph_fluid_setting.png

图 23.3 本章考虑的流体场景#

我们现在考虑如图 23.3 所示的流体场景：重力作用下水在方形容器内的运动。我们将水所占据的空间称为流体域，容器内除去流体域的部分充满了空气。由于空气密度远低于水，一般的物理模拟算法会忽略它的作用，因此我们仅需将流体域用粒子填满。

设系统中包含 \(n\) 个粒子，在流体模拟中，每个粒子 \(i\) 需要携带的信息包括它所代表流体微团的质量 \(m_i\)、所在位置 \(\boldsymbol x_i\) 以及速度 \(\boldsymbol v_i\)。仅使用这三个物理量我们就能够计算出所有流体模拟所需要的物理量，如密度场和压强场，而这离不开我们为粒子系统配备的一个强大的工具——核函数。

23.2.1.1. 核函数#

光滑粒子流体动力学的一大优点已经体现在它的名字当中——光滑，之所以称为“光滑粒子”，就是因为采用它的离散格式所近似出来的场是光滑的。如果想要用一群均匀采样的粒子离散一个标量场，最直接的想法便是在每个粒子的位置上采样，对于不在粒子上的点，用离它最近的粒子上的值来近似——这个方法的一个致命缺点就是它不连续，每个粒子都对应于一个区域，区域内任一点到该粒子最近，在这个区域的边界上就会有数值的跳变（因为“最近粒子”变成了另一个），在流体模拟中这会带来很不自然的模拟效果。既然每个位置上的取值只依赖于一个粒子会带来不连续性，那么为了“平滑”这种不连续性，我们可以让取值依赖于附近的多个粒子，并且可以很自然地想到，离得越远的粒子权重越低，这样在我们连续移动取值点时，离得远的粒子的进出就不会带来太多数值变化，从而就可以实现连续了。

光滑粒子流体动力学的核函数采用的正是这一思想，它一般是一个定义在球形邻域上的非负函数，并且越靠近邻域的边界值越接近 \(0\)，如图 23.4 所示。核函数正是为了给邻居粒子上的值加权，为了保证乘上权重之后不会导致数值被无故地放大或缩小，一般核函数 \(W\) 的选取要满足在 \(d\) 维空间下有 \(\int_{\mathbb R^d}W\left(\Vert\boldsymbol x\Vert\right)\mathrm d\boldsymbol x=1\)。

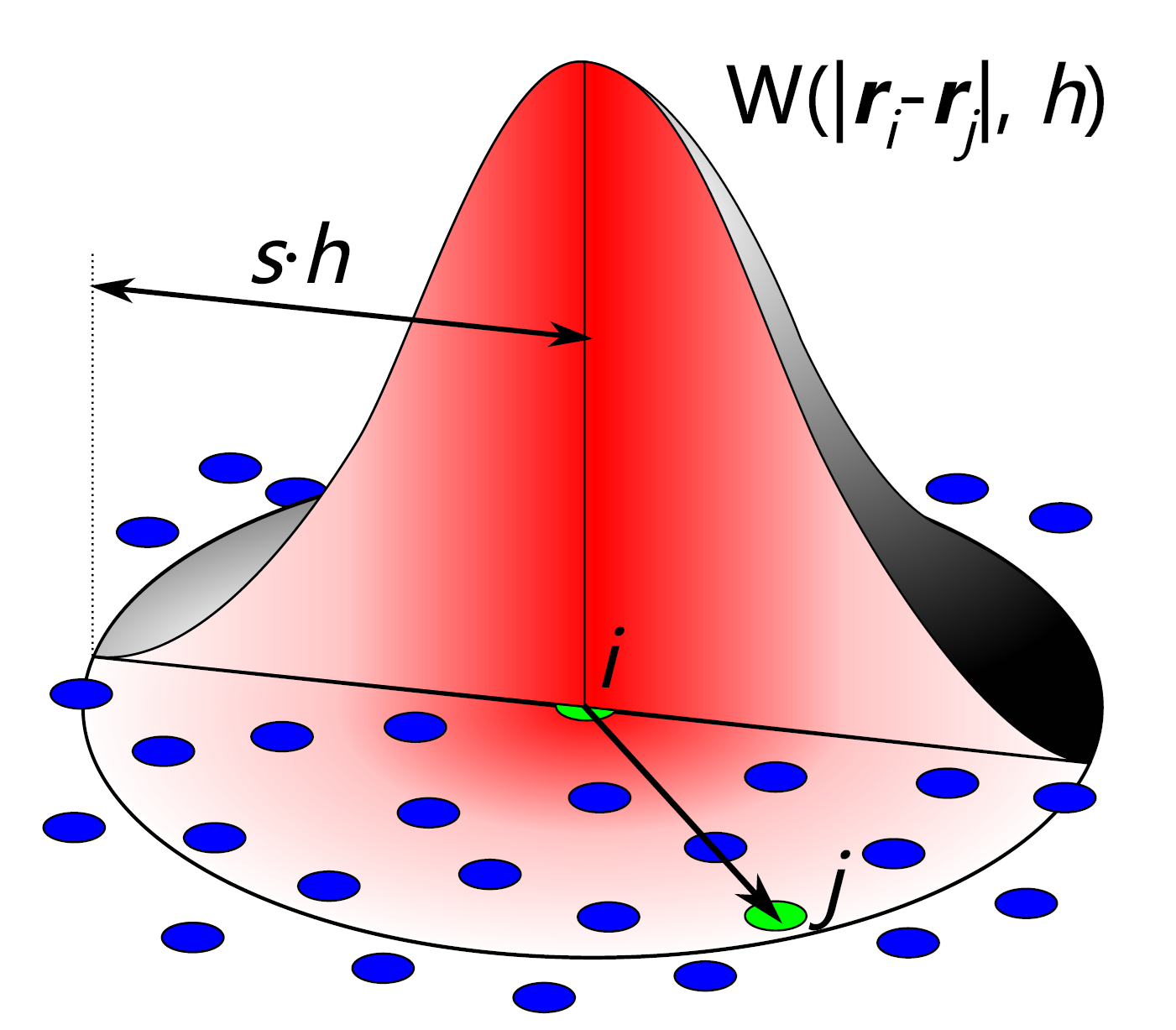
../../_images/animation-fluids-kernel_function.png

图 23.4 核函数 [1]#

一个常用的核函数表达式如下，其名称为三次样条核函数（cubic spline kernel）：

(23.4)#\[\begin{split} W_\mathrm{cubic}(r,h)=\sigma \begin{cases} 6(q^3-q^2)+1&0\le q\le\frac 12\\ 2(1-q)^3&\frac 12<q\le 1\\ 0&\text{otherwise} \end{cases}， \end{split}\]

其中 \(q=\frac rh\)；\(h\) 为核半径，超过该半径范围的部分核函数值为 \(0\)；\(\sigma\) 为一归一化系数，在一维空间中取 \(\frac 4{3h}\)，在二维空间中取 \(\frac{40}{7\pi h^2}\)，在三维空间中取 \(\frac 8{\pi h^3}\)。在实践中，一般取 \(h\) 为一固定长度 \(h_0\)（如 \(1\) 到 \(3\) 倍初始状态下相邻粒子的平均间距），然后令 \(W(r)=W_\mathrm{cubic}(r,h_0)\)。

23.2.1.2. 密度场与压强场#

有了核函数之后，我们就可以通过粒子的位置和质量来估计出密度场：

(23.5)#\[ \rho(\boldsymbol x)=\sum_im_iW\left(\Vert\boldsymbol x-\boldsymbol x_i\Vert\right)。 \]

类似地，我们通过以下式子估算压强场和压强的梯度：

(23.6)#\[ p(\boldsymbol x)=\sum_ip_i\frac{m_i}{\rho_i}W\left(\Vert\boldsymbol x-\boldsymbol x_i\Vert\right)， \]
(23.7)#\[ \nabla p(\boldsymbol x)=\sum_ip_i\frac{m_i}{\rho_i}\nabla W\left(\Vert\boldsymbol x-\boldsymbol x_i\Vert\right)， \]

其中

(23.8)#\[ p_i=k(\rho_i-\rho_0)^\gamma， \]

这里的 \(k\) 和 \(\gamma\) 均为常数，\(\rho_0\) 为流体的静止密度。物理量 \(p_i\) 表示粒子 \(i\) 处的压强大小，它随粒子密度 \(\rho_i\) 的增加而增加，那么纳维-斯托克斯方程中的压强项\(-\nabla p\) 就会将粒子从密度高的地方推向密度低的地方，以维持一个近似不可压的状态。

式 (23.8) 中计算压强的方法被称为状态方程（equation of state，EOS）法，这样计算出来的压强不能够维持一个严格的无散速度场，所以模拟出来的流体实际上是弱可压（weakly compressible）流体。当然，我们可以通过调节 \(k\) 和 \(\gamma\) 来调整流体有多不可压。

学术界有许多求解 \(p_i\) 的方法能够保证光滑粒子流体动力学模拟的不可压性质，这些方法一般基于连续方程（continuity equation）求解流体速度场的矫正，使流体的密度场在模拟过程中保持恒定，如隐式不可压光滑粒子流体动力学（implicit incompressible SPH，IISPH）[ICS+14]、预测-矫正不可压光滑粒子流体动力学（predictive-corrective incompressible SPH，PCISPH）[SP09]、无散光滑粒子流体动力学（divergence-free SPH，DFSPH）[BK17] 等。这些方法模拟出来的流体会更加接近真实水的效果，不会出现粒子“一弹一弹”的类似果冻的现象。

另外，我们还可以用下式替换式 (23.7) 来求压强梯度：

(23.9)#\[ \nabla p(\boldsymbol x_i)=\rho_i\sum_jm_j\left(\frac{p_i}{\rho_i^2}+\frac{p_j}{\rho_j^2}\right)\nabla_iW\left(\Vert\boldsymbol x_j-\boldsymbol x_i\Vert\right)， \]

这个式子的好处在于任意两个粒子给对方的作用力大小相等、方向相反，从而能够保证整个系统是动量守恒的。尽管式 (23.9) 不是对压强直接求梯度得到的结果，但也是一个足够好的近似，加上动量守恒的良好性质，能够取得比式 (23.7) 更好的视觉效果。

23.2.2. 算法流程#

作为总结，我们给出在光滑粒子流体动力学模拟中，每个时间步需要执行的步骤：

  1. 用粒子受到的外力更新速度 \(\boldsymbol v_i\gets\boldsymbol v_i+\Delta tm_i\boldsymbol g\)，然后用速度更新粒子位置 \(\boldsymbol x_i\gets\boldsymbol x_i+\Delta t\boldsymbol v_i\)。

  2. 用式 (23.5) 计算每个粒子处的密度\(\rho_i=\rho(\boldsymbol x_i)\)。

  3. 用式 (23.8) 计算每个粒子处的压强。

  4. 用式 (23.7) 或式 (23.9) 计算压强梯度 \(\nabla p(\boldsymbol x_i)\)，从而得到每个粒子受到的压力 \(\boldsymbol f_i=\frac{m_i}{\rho_i}\nabla p(\boldsymbol x_i)\)。

  5. 用压力更新粒子速度和位置 \(\boldsymbol v_i\gets\boldsymbol v_i+\Delta t\boldsymbol f_i\)，\(\boldsymbol x_i\gets\boldsymbol x_i+(\Delta t)^2\boldsymbol f_i\)。