离散微分几何

11.1. 离散微分几何#

离散微分几何（Discrete Differential Geometry，DDG）是几何处理的数学基础。传统的微分几何是在连续空间中的进行几何分析的，如光滑的参数化曲面，而计算机中的一切量都是离散的，如由连续曲面离散化成的三角网格，离散微分几何就是将二者进行联系的桥梁。 这里我们会简单介绍离散微分几何中几个比较基础的微分量。

在连续域的几何分析中，通常会定义一些有着独特性质和重要应用的微分量，但对于离散的三角网格而言，在边或顶点的连接处，很多微分量是没有良定义的，因为由三角网格定义出的几何形状只能给出 \(\mathcal{C}^0\) 连续性。因此，如何将它们应用在离散的情况上是离散微分几何的研究重点。 这部分我们将介绍如何在三角形网格上定义以及计算一些连续微分量的离散近似，从而为后面的几何处理提供数学帮助。离散微分几何博大精深，本章无法完全覆盖，我们推荐感兴趣的同学观看 CMU 的 DDG 课程：https://brickisland.net/DDGSpring2022/ 。

11.1.1. 局部平均区域#

首先，我们介绍局部平均区域（local averaging region）。 为了定义三角网格顶点上的微分量，我们考虑从积分的角度来描述它： 我们计算这个微分量在顶点周围邻域内的积分值，然后假定该微分量在顶点周围邻域内变化很小，可以被近似看成一个定值，于是将积分值除以邻域面积，就可以得到该微分量。

记该顶点为 \(\mathbf x\)，顶点邻域的选取方法会直接影响到离散微分量的结果和准确度：若选取的邻域较大，那么得到的微分量在空间上会更为平滑，若选取的邻域较小，得到的微分量会更加准确，同时对于网格上的噪声也会更加敏感。 图 11.1 展示了较为常见的三种定义邻域的方式。

  • 重心单元（barycentric cell），即把三角形的两边的中点和三角形的重心顺次连起来。

  • 泰森多边形单元（Voronoi cell），是由每条边的中垂线确定的区域，根据中垂线的性质，每个三角形内，蓝色区域中的点到\(x\)的距离都会小于另两个顶点。但是正如图中所示，若顶点周围存在钝角三角形，则蓝色区域会超出三角形。

  • 混合泰森多边形单元（mixed Voronoi cell）是对上一种方法的改进，在出现钝角三角形时，用三条边的中点连线来框选出该三角形内的蓝色区域。

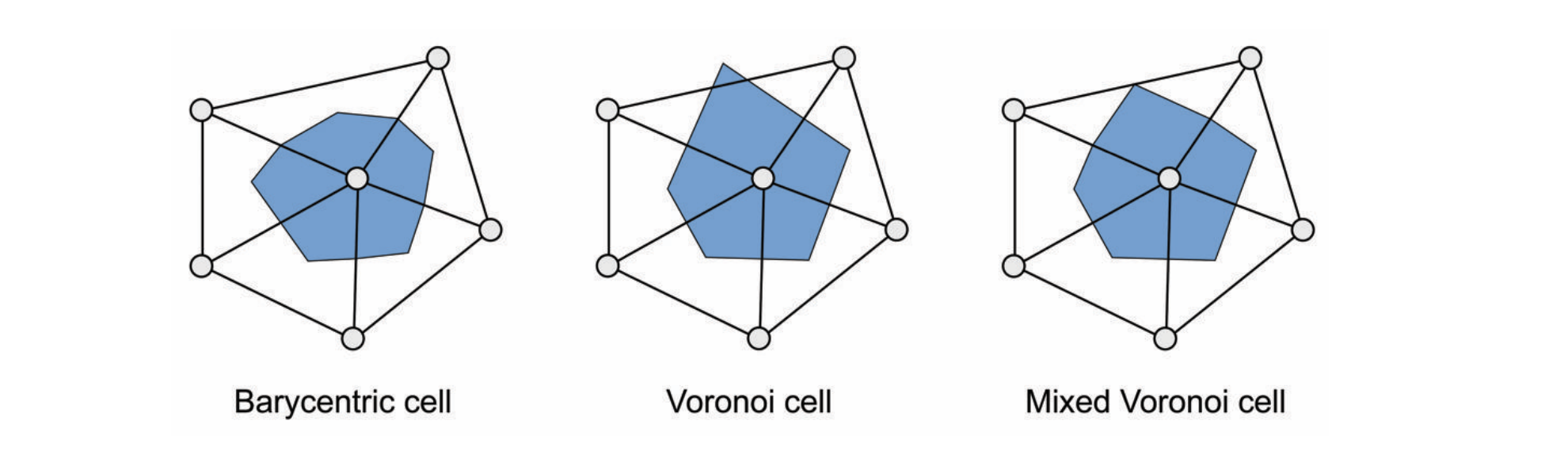
../../_images/local_average.png

图 11.1 计算局部平均区域时对顶点邻域的三种选取方式，所选定的邻域用蓝色标出。#

11.1.2. 法向量#

(11.1)#\[ \mathbf n (\mathbf x) =\frac{\sum_{T\in \Omega(\mathbf x)}\alpha_T\mathbf n (T)}{\lVert \sum_{T\in \Omega(\mathbf x)}\alpha_T\mathbf n (T) \rVert}， \]

其中，\(\Omega(\mathbf x)\) 是与顶点 \(\mathbf x\) 邻接的三角形的集合，\(\alpha_T\) 及 \(\mathbf n (T)\) 分别是三角形 \(T\) 的权重和法向量。 对于权重 \(\alpha_T\) 的选择有很多方式，常见的有以下三种：

  1. \(\alpha_T=1\)。取常数权重是最容易计算的，不过这种取法没有考虑任何三角形的信息，对于不规则的网格会得到一些反常的结果。

  2. \(\alpha_T=\text{area}(T)\)。根据三角形面积大小进行加权比常数权重更加合理，且面积大小可以通过两条边叉乘得到，便于计算。但遇到过于不规则的网格时这种做法也不够可靠。

  3. \(\alpha_T=\theta(T)\)。根据三角形对应顶点\(\mathbf x\)处的角度进行加权可以给出更好的结果，不过这种做法计算起来比较麻烦。

11.1.3. 梯度#

梯度是非常重要的一阶微分量，在计算拉普拉斯算子以及网格参数化、网格形变中都有着重要的作用。

对单个三角形而言，给定三个顶点 \(\mathbf x_i,\,\mathbf x_j,\,\mathbf x_k\) 上的函数值 \(f_i,\,f_j,\,f_k\)，则在三角形内部任一点 \(\mathbf x\) 上的函数值 \(f(\mathbf x)\) 可以根据点 \(\mathbf x\) 的重心坐标（barycentric coordinate）进行线性插值得到：

(11.2)#\[ f(\mathbf x)=\alpha(\mathbf x)f_i+\beta(\mathbf x) f_j +\gamma(\mathbf x) f_k \]

其中权重 \(\alpha,\,\beta,\,\gamma\) 是点 \(\mathbf x\) 关于顶点 \(\mathbf x_i,\,\mathbf x_j,\,\mathbf x_k\) 的重心坐标，且满足 \(\alpha +\beta + \gamma =1\)。如 图 11.2 所示定义，重心坐标表征的是该点到各顶点的相对位置，一组重心坐标可以唯一地确定三角形中的一点。

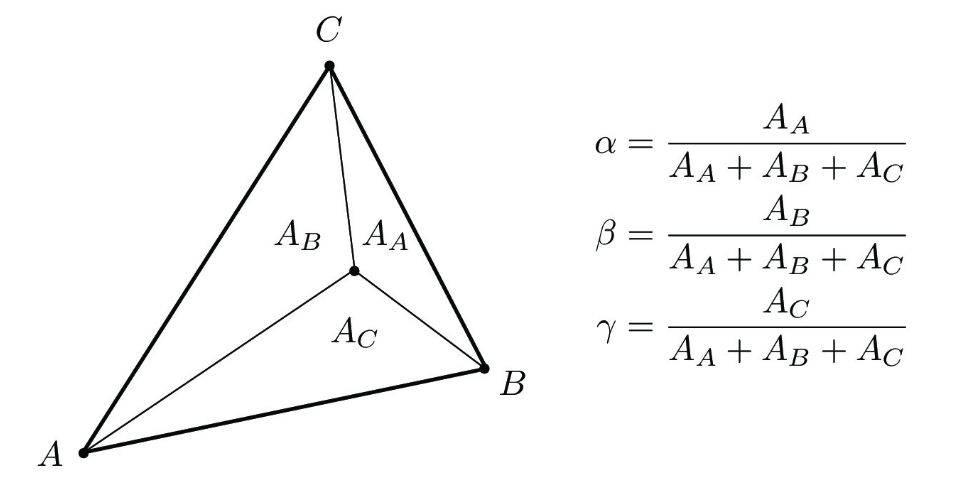
../../_images/barycentric.png

图 11.2 重心坐标 \(\alpha(\mathbf x)\) 的值等于绿色部分三角形与整个三角形的面积之比。#

那么函数 \(f(\mathbf x)\) 的导数为：

(11.3)#\[ \nabla_\mathbf x f(\mathbf x)=f_i \nabla_\mathbf x \alpha+f_j \nabla_\mathbf x \beta + f_k \nabla_\mathbf x \gamma \]

代入重心坐标的表达式可以算得：

(11.4)#\[ \nabla_\mathbf x f(\mathbf x)=(f_j-f_i)\frac{(\mathbf x_i-\mathbf x_k)^{\bot}}{2A_T}+(f_k-f_i)\frac{(\mathbf x_j-\mathbf x_i)^{\bot}}{2A_T} \]

其中 \(\bot\) 表示在三角形平面上旋转 \(90\) 度，\(A_T\) 是三角形的面积，推导过程此处不再赘述。可以看出，经过线性插值得到的 \(f(\mathbf x)\) 的梯度在一个三角形内是定值。

11.1.4. 离散拉普拉斯算子#

拉普拉斯算子（Laplace-Beltrami operator）是一个非常重要的工具，涉及几何处理的方方面面，包括网格滤波、参数化、压缩、差值以及模拟等等。拉普拉斯算子被定义为函数梯度的散度：

(11.5)#\[ \Delta f = div\nabla f \]

对于标量函数来说，即 \(\Delta f =\sum_i\frac{\partial^2 f}{\partial x_i^2}\in \mathbb R\)。 从定义中可以看出，拉普拉斯算子是一个二阶微分量。拉普拉斯算子应用在标量函数上表达的是函数的趋势，应用在几何表面上刻画的就是几何形状的走向。例如，我们可以通过拉普拉斯算子来定义曲面的平均曲率 \(H\)，它刻画的是曲面某处的弯曲程度。记函数 \(\mathbf S\) 是映射到三维空间中的曲面，曲面上某点处的平均曲率为 \(H\)，法向量为 \(\mathbf{n}\)，则有：

(11.6)#\[ \Delta \mathbf S =-2 H \mathbf{n}\in \mathbb R^3 \label{eq:qulv} \]

在离散情形下，由于三角形面内的梯度是定值，所以拉普拉斯算子恒为 \(0\)。因此我们通常从三角形顶点的值出发研究拉普拉斯算子。利用二阶差分的思想，函数 \(f(\mathbf x_i)\) 在顶点 \(\mathbf x_i\) 处的拉普拉斯算子的一般形式可以写成：

(11.7)#\[ \Delta f_i = \sum_{j \in \Omega(i)} \omega_{ij}(f_j-f_i) \]

这里，\(\omega_{ij}\) 是标量权重，\(\Omega(i)\) 是顶点 \(\mathbf x_i\) 的邻居顶点集合。不同权重选取方式对应着不同的离散拉普拉斯算子，这里我们介绍其中两种。

11.1.4.1. 均匀拉普拉斯#

均匀拉普拉斯（uniform Laplacian）是最简单的一种形式，它将权重取为定值，定义为：

(11.8)#\[ \Delta f_i = \sum_{j \in \Omega(i)} (f_j-f_i)/N_i \]

其中 \(N_i\) 表示邻居顶点的数量。均匀拉普拉斯算子计算的是函数 \(f\) 从 \(\mathbf x_i\) 到其所有周围顶点 \(\mathbf x_j\) 的差的平均值。 这种定义方法便于高效计算，并且被用于滤波等几何处理。但实际上它并不是一种恰当的定义方式，例如，对于平面而言，由于曲率为 \(0\)，按照连续情形下的公式 (11.6)，它的拉普拉斯的值也应该为 \(0\)，但对平面进行不规则的离散化后，很明显式 (11.8) 不一定满足这个要求。也就是说，我们不能保证一个平面经过三角网格划分后，网格顶点 \(\mathbf x_i\) 一定处于它所有邻居的中心。

11.1.4.2. 余切拉普拉斯#

../../_images/cal_suanzi.png

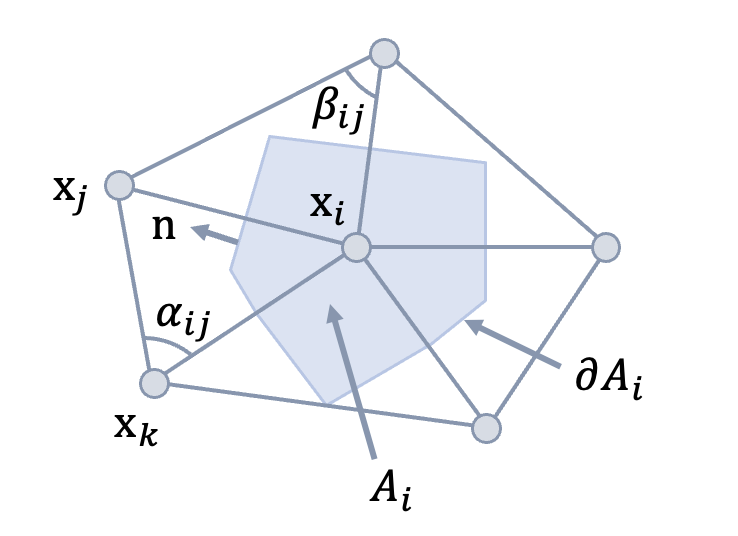
图 11.3 计算余切拉普拉斯算子的方式。#

一种更加合理的离散拉普拉斯算子定义方式是通过局部平均区域思想得到的余切拉普拉斯（cotangent Laplacian），它可以通过混合有限元（mixed finite element）或者有限体积（finite volume）方法得到。 为了简化积分的运算，我们需要用到高斯散度定理：

\[ \int_{A_i} (\Delta f)dA = \int_{A_i} div (\nabla f)dA = \int_{\partial A_i} (\nabla f) \cdot \mathbf{n}ds \]

在计算的时候，我们分别考虑每个三角形的积分，如 图 11.3 所示，因为在一个三角形网格上，梯度是不变的，同时带入法向的定义：

\[ \int_{\partial A_i \cap T} (\nabla f) \cdot \mathbf{n}ds = \frac{1}{2}(\nabla f)\cdot(\mathbf{a}-\mathbf{b} )^\bot = \frac{1}{2}(\nabla f)\cdot(x_j-x_k)^\bot \]

将梯度的定义带入其中，得到

\[ \int_{\partial A_i \cap T} (\nabla f) \cdot \mathbf{n}ds =\frac{1}{2}(cot\gamma_k(f_j-f_i)+cot\gamma_j(f_k-f_i)) \]

其中，\(\gamma_k,\gamma_j\) 是点 \(x_k,x_j\) 处的三角形内角。 因此

\[ \int_{\partial A_i} (\nabla f) \cdot \mathbf{n}ds = \frac{1}{2}\sum_{j\in \Omega(i)}(cot\alpha_{ij}+cot\beta_{ij})(f_j-f_i) \]

由于假定拉普拉斯算子在所选取的区域内是个定值，因此我们可以得到它在顶点 \(\mathbf x_i\) 上的值为：

\[ (\Delta f)_i = \frac{1}{2A_i} \sum_{j\in \Omega(i)}(cot\alpha_{ij}+cot\beta_{ij})(f_j-f_i) \]

这种拉普拉斯算子会满足公式 (11.6) 的性质，也是应用最广的一种形式。 值得注意的是，当式中两个角度大于 \(\pi\) 时，\((cot\alpha_{ij}+cot\beta_{ij})\) 会变为负数，这会导致一些三角形发生旋转，在计算时需要进行特殊处理。