19.2. 运动学#
在主观动态的场景中，大多数运动的对象可以被表示成一个铰链刚体，即由关节连接的一系列刚体（我们在 §22.3 中还会探讨这类物体的模拟）。以人体为例，我们会将足部、大腿、小腿等在运动中几乎不产生形变的部位视为刚体，将膝、肘、脖子等关节视为铰链，如图 19.10 所示。
图 19.10 人体的铰链刚体结构#
本节会以图 19.10 中的结构为例介绍一些处理这种铰链刚体运动状态的基本方法。运用这些方法，对于任意一个角色，只要我们能够抽象出它的骨架（即铰链刚体结构），就能够为它摆好姿态，进而使其活动起来。
19.2.1. 前向运动学#
我们进一步将图 19.10 中的人体结构抽象化，将每个关节看成一个节点、每个骨骼看成一条边，则可以转换成图 19.11 所示的树结构。选定腰部关节作为整棵树的根节点，那么其余所有节点可以确定其唯一的父节点，并且每个节点的状态（即位置和全局朝向）可以从其父节点的状态推算出来；因此，只要我们知道了根节点的位置以及每个节点所对应关节的旋转，就可以从根开始向下遍历整棵树，推出所有关节的状态——这个过程又称为前向运动学（forward kinematics）。
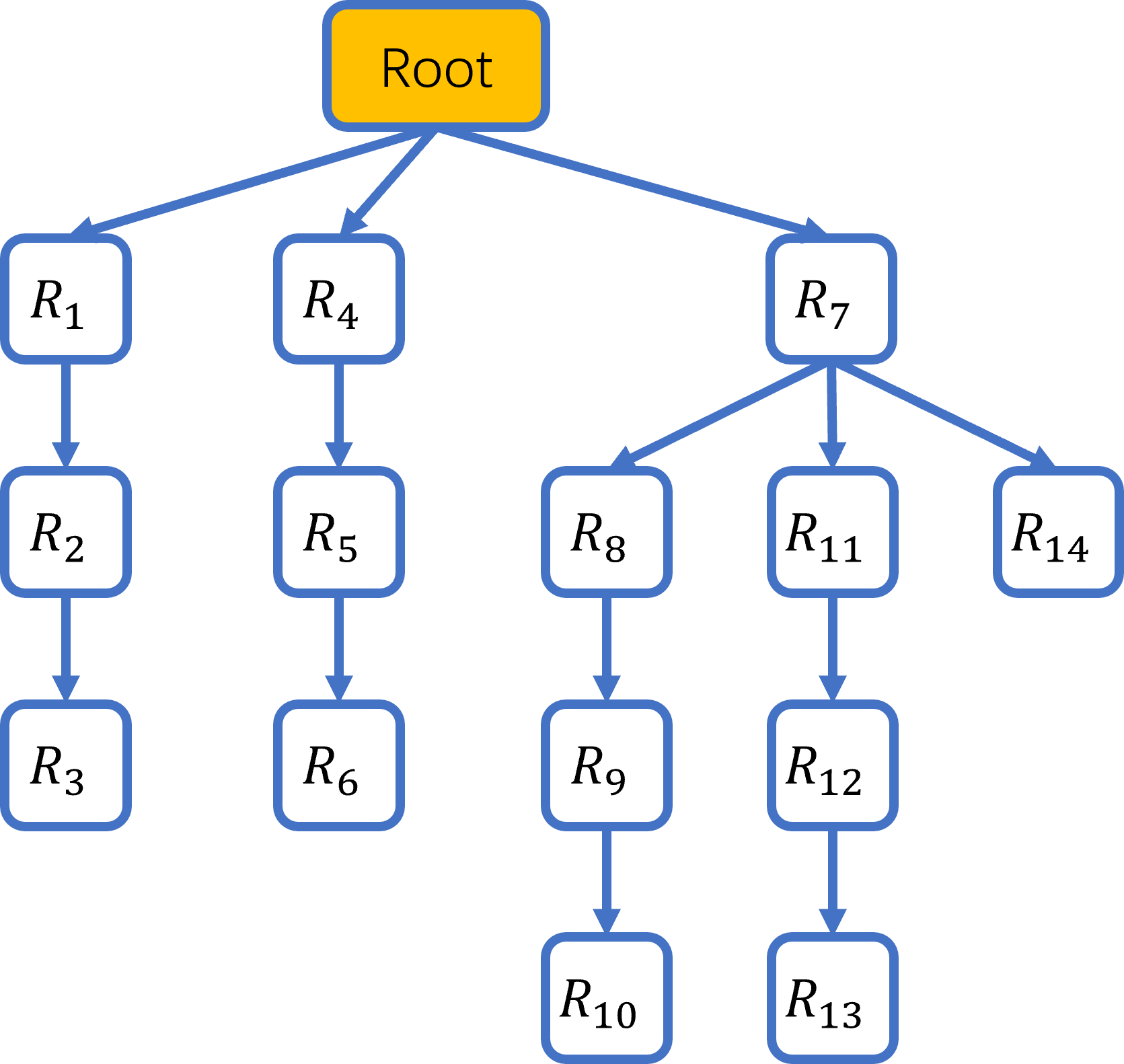关节与骨骼形成的树结构
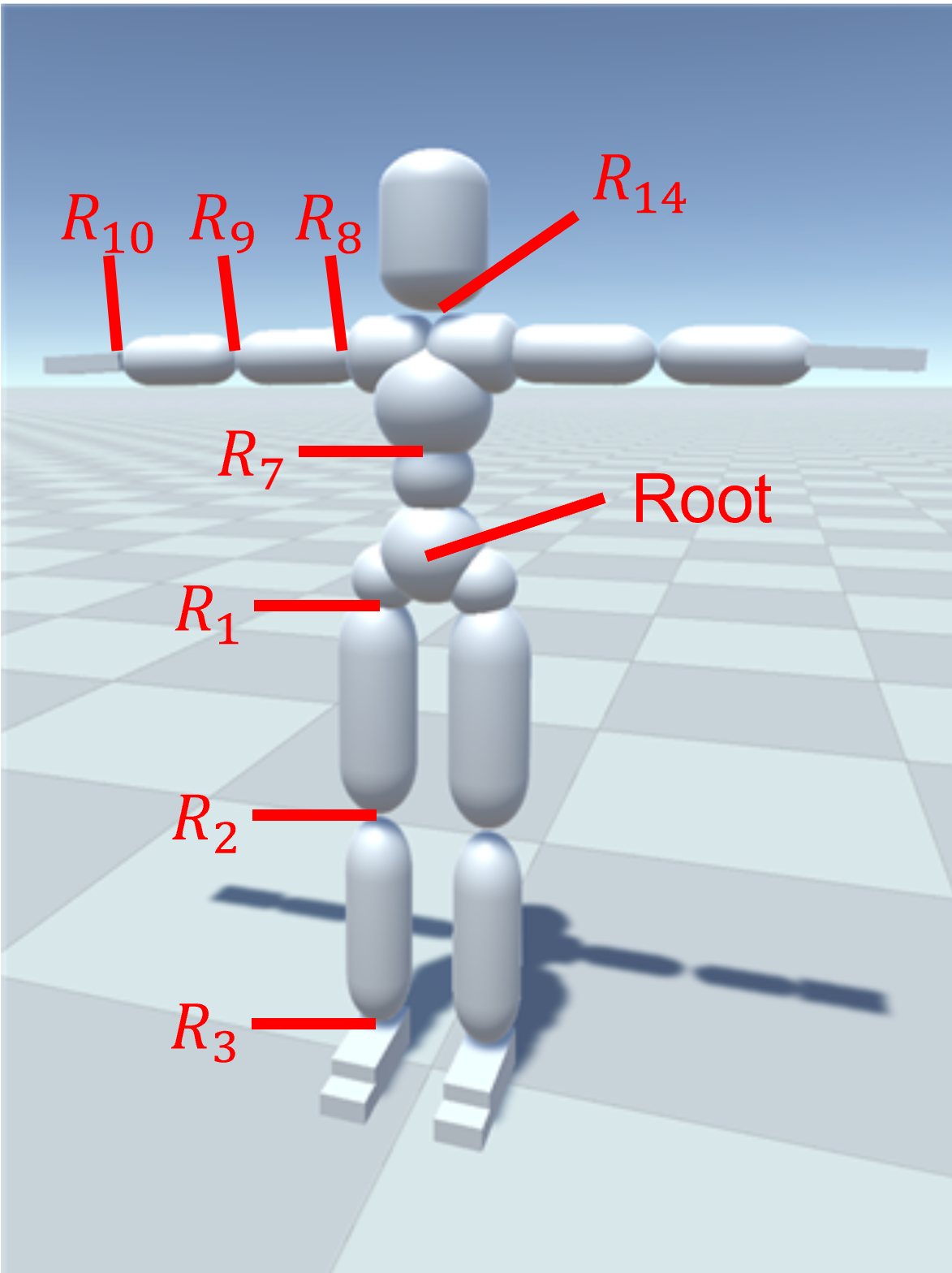树的顶点与关节之间的对应
定义一个三维空间下的正交坐标系 \(xyz\)，称关节相对于 \(xyz\) 坐标系的旋转为全局旋转，其自身为子树内全部骨骼以及关节带来的旋转为局部旋转。在本节，我们一律使用四元数表示旋转。当所有关节的旋转为 \([1,\boldsymbol 0]\) 时，整个系统处于初始姿态。对于人体我们常常把这个初始姿态定义成图 19.10 所示的姿态，即身体直立且手臂平举；这个姿态形似英文字母“T”，因此又被称为 T 型姿势（T-pose）。
现在我们以图 19.12 中展示的铰链刚体为例展示前向运动学的计算过程。这个铰链刚体包含三根骨骼、四个关节，将四个关节记为 \(P_0\sim P_4\)，它们的位置记为 \(\boldsymbol p_0\sim\boldsymbol p_4\)，相邻两个关节的相对位移记为 \(\boldsymbol l_{0\sim 1}\sim\boldsymbol l_{2\sim 3}\)，三根骨骼的长度就是这些相对位移的模长 \(l_{0\sim 1}\sim l_{2\sim 3}\)。
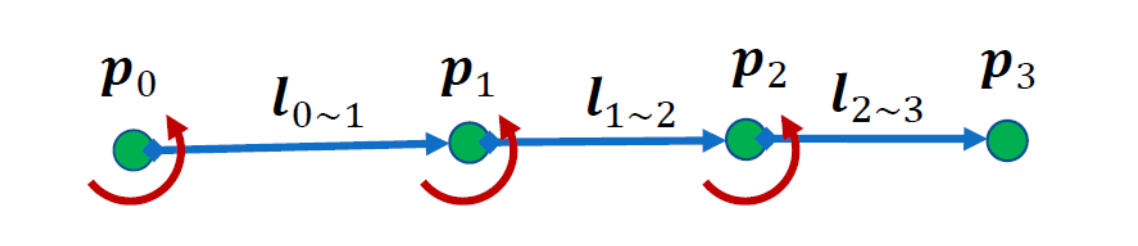简化铰链刚体的初始姿态
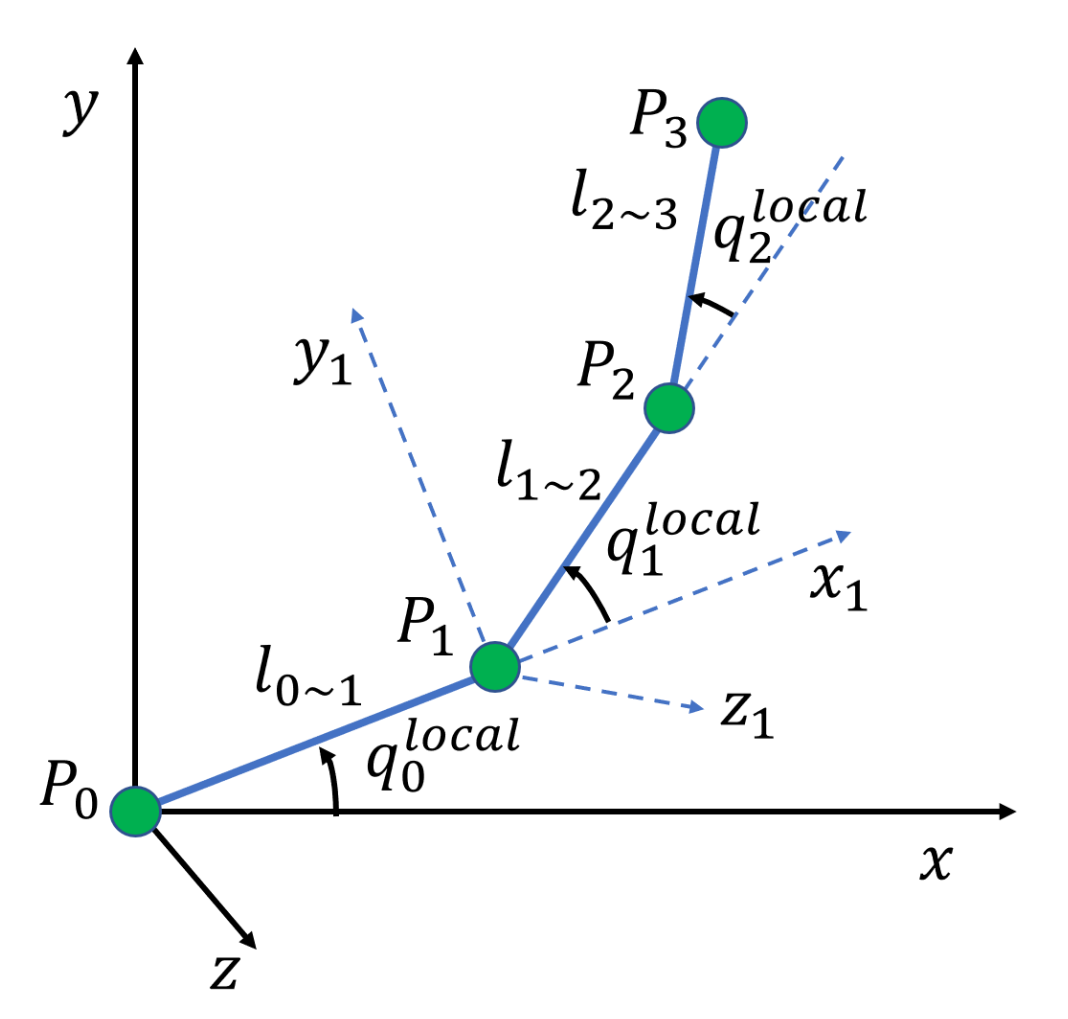简化铰链刚体的某一个姿态
图 19.12 简化的铰链刚体系统#
令 \(P_0\) 为根关节，那么在这个例子中，对于 \(i\in\{1,2,3\}\)，关节 \(i\) 的父关节即为 \(i-1\)，有如下关系：
在初始姿态下，铰链刚体的所有关节和骨骼共线，我们不妨以根关节为原点、铰链刚体初始姿态下的指向为 \(x\) 轴构建坐标系 \(xyz\)，那么初始状态下每个骨骼带来的相对位移即为
为了让铰链刚体摆出一个特定的姿态，我们会为除了 \(P_3\) 的每个关节指定一个局部旋转，这个局部旋转会带动其后的全部关节和骨骼整体旋转，记这些局部旋转为 \(q_0^\mathrm{local}\sim q_2^\mathrm{local}\)。据此我们可以计算出所有关节的全局旋转。首先跟关节的全局旋转等于局部旋转，即 \(q_0=q_0^\mathrm{local}\)；对于非根关节，其局部旋转即为相对于父关节上固连的坐标系的旋转，因此全局旋转即为先进行局部旋转再进行父关节的全局旋转的复合结果，因此有 \(q_i=q_{i-1}q_i^\mathrm{local}\)（\(i\in\{1,2\}\)）。根据全局旋转，我们可以进一步求出骨骼带来的相对位移 \(\boldsymbol l_{(i-1)\sim i}\) 即为 \(q_{i-1}\left[0,\boldsymbol l_{(i-1)\sim i}^\mathrm{init}\right]q_{i-1}^\star\) 的虚部（\(i\in\{1,2,3\}\)）。至此我们不难求出每个关节的全局坐标。
在角色动画领域，人们常用的动捕文件格式——BVH 文件（BioVision Hierarchy 文件）——就是基于前向运动学的原理。这种动捕文件会包含一个铰链刚体在每个关节局部旋转均为 \([1,\boldsymbol 0]\) 时的初始状态信息，以及一段动作序列的每一帧的运动信息。每一帧的运动信息又包含根关节的位移，以及所有关节的局部旋转；我们需要借助前向运动学才能从动捕数据中恢复出完整的角色姿态。BVH 文件格式我们后面还会在 §20.2.1 中详细介绍。
19.2.2. 关键帧动画#
在学习了前向运动学之后，我们知道可以使用关节旋转和根节点位移的序列，来表示一段连续的动作序列。但是如果一段动作序列每一帧的信息都需要我们挨个输入，那么无论是时间成本还是制作成本，都会变得非常高昂。
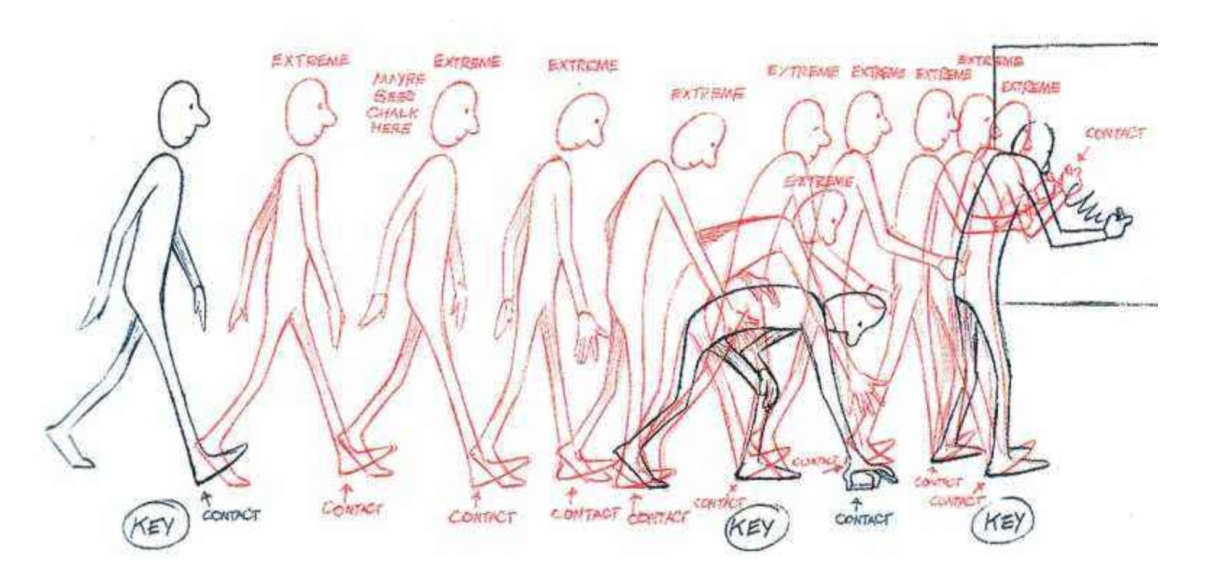
图 19.13 关键帧动画#
在手工绘制动画的时代，动画画师也会遇到相同的问题，针对该问题动画界给出的答案是中间画（in between）。动画师只绘制包含关键转折在内的关键帧，而在关键帧之间的起到衔接过渡的较为次要的动画，会由另一批画师绘制。这样子便可以让多个画师同时参与动画的绘制，同时能够较好地解决画师之间不同风格带来的问题。
类似于中间画的做法，运动学上也可以只编辑关键帧，通过关键帧之间进行插值的方式来降低生成动画的复杂性，但是此时我们可以使用计算机进行自动的中间动画生成。针对根节点的位置，我们可以采用贝塞尔曲线的方式对于根节点所处的位置进行插值。针对关节的旋转，我们则可以使用球面线性插值公式 (19.10) 进行更为平滑的旋转插值，也可以进一步的将贝塞尔曲线的思想应用到旋转插值上。由于关键帧之间不存在较为显著的位置，旋转的突变，因此使用上述算法进行动作的平滑过渡即可实现很好的插值结果。
19.2.3. 逆向运动学#
我们在前面学习的前向运动学所解决的问题是：根据根节点的位置以及关节的局部旋转，还原出所有关节的位置。而逆向运动学（inverse kinematics，IK）的任务恰恰相反，其需要根据给定的部分关节的位置（包括但不限于末关节），反向求解出一组关节局部旋转的解。逆向运动学可以被用于机械臂或者是虚拟角色的控制，也可以帮助修复一些质量较差，没有满足部分接触要求的动作捕捉数据。
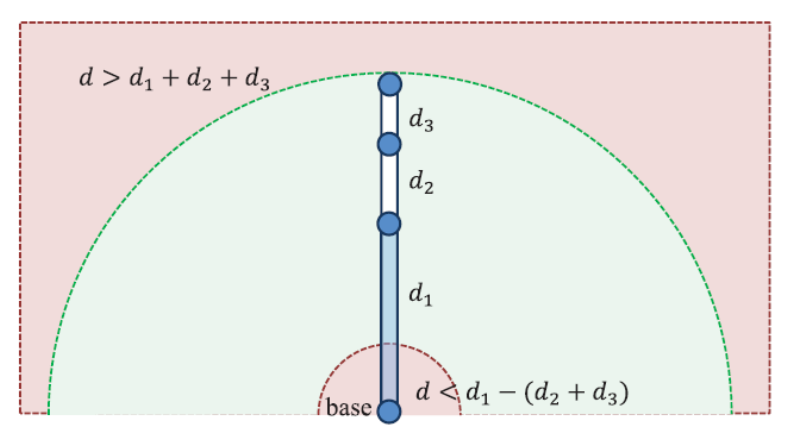
图 19.14 末端点在红色区域内时系统无解#
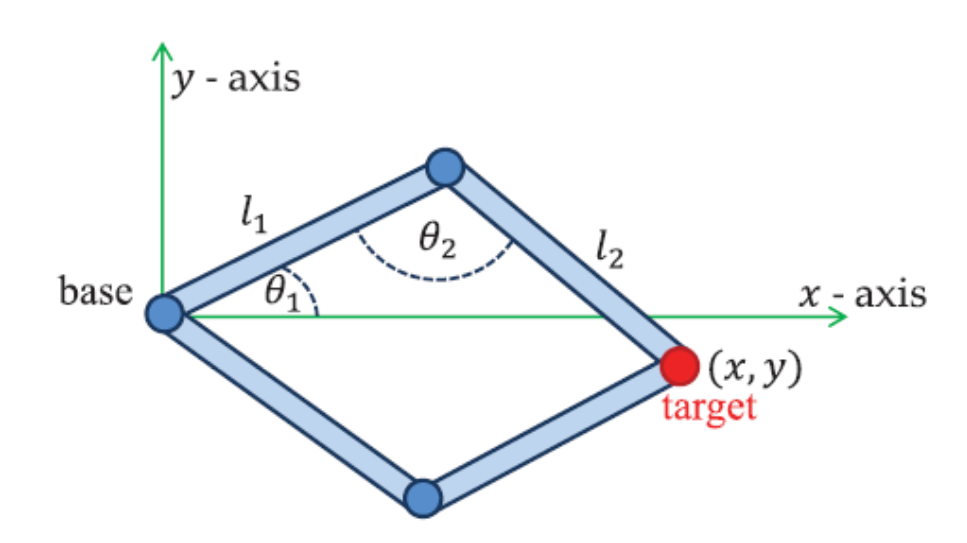
图 19.15 系统存在两个不同的解#
相比于前向运动学，逆向运动学面临最大的挑战便是解空间的复杂性。一方面，由于铰接刚体系统自身的限制，并不是对于任意的关节位置要求，都存在一种合法的关节旋转，如图 19.14 所示。另一方面，对于有解的关节位置要求，很可能存在多种不同的解，如图 19.15 所示；而此时我们希望能够选取出更为自然的解，一般来说，我们会更倾向于关节旋转更为平滑，相邻帧解更为接近的方案。
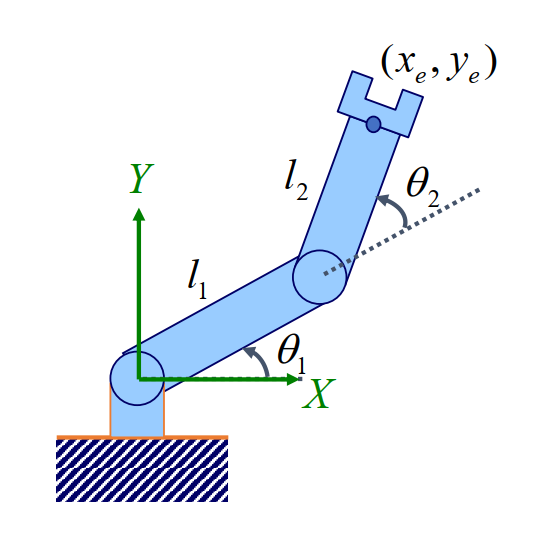
图 19.16 双骨骼系统#
我们以较为简单的二维双骨骼系统为例介绍逆向运动学的概念。如图 19.16 所示，双骨骼系统由三个关节与两个骨骼组成，利用前向运动学不难得到其末端关节的位置：
在给定末端关节位置后（即 \(x_\mathrm e\)、\(y_\mathrm e\) 已知），我们可以代入 \(x_\mathrm e\) 和 \(y_\mathrm e\) 的值求出 \(\theta_1\) 和 \(\theta_2\)。当然还有另外一种思路：三个关节两两之间的距离都已经确定，因此我们可以唯一确定三个关节所确定的三角形，根据三角形的内角以及图 19.15 所示的两种解之下的角度关系，进而求出 \(\theta_1\) 和 \(\theta_2\)。
对于二维情形下仅包含两个骨骼的逆向运动学任务，我们可以求出关节局部旋转的解析式，但是对于骨骼数量大于两个的逆向运动学任务，并不存在关节角度的解析解。因此，我们只能通过设计一些迭代算法从数值上不断逼近这个解，接下来我们将依次介绍三种迭代方法，分别是循环坐标法（cyclic coordinate descent，CCD）、前向和后向迭代逆运动学（forward and backward reaching inverse kinematics，FABRIK）以及雅可比矩阵法（Jacobian inverse kinematics，Jacobian IK）。在接下来的部分，为简化问题，我们均假设铰链刚体是一个链状结构。
19.2.3.1. 循环坐标法#
循环坐标法求解逆向运动学问题的思想是：每次迭代调整一个关节，使得该关节旋转后，末端距离目标点尽可能接近。具体来讲，假设铰链刚体拥有标号为 \(0\sim n\) 的 \(n+1\) 个关节，与 \(n\) 个连接关节的骨骼，我们希望末端的 \(n\) 号关节距离目标 \(\boldsymbol t\) 尽可能地接近，记关节的位置为 \(\boldsymbol p_0\sim\boldsymbol p_n\)。循环坐标法会按照 \(n-1,n-2,\cdots,0\) 的顺序依次调整关节的局部旋转，设当前正在调整 \(i\) 号关节的旋转，则当且仅当 \(\boldsymbol p_i\)、\(\boldsymbol p_n\)、\(\boldsymbol t\) 三点共线时末端关节与目标位置最近，据此可以计算出需要对 \(i\) 号关节施加的旋转。将上述过程重复若干轮，即可逐渐逼近目标点。
例如，我们目前有一个三个骨骼的系统，并希望将该系统末端节移动到位于红色圈处的目标，如图 19.17(a) 所示。首先我们旋转从根节点开始的第三个关节，使得最后一根骨骼对准目标点，也就是第三，四个关节和目标点三点共线，因为此时末端关节距离目标点的距离是最近的。第一次旋转如图 19.17(b) 所示。之后我们旋转从根节点开始的第二个关节，固定第三个关节，使得第二，四个关节和目标点三点共线。第二次旋转后如图 19.17(c) 所示。最后我们旋转根节点，使得第一，四个关节和目标点三点共线。第三次旋转后如图 19.17(d) 所示。经过三次旋转，我们成功地将末端点移动到了一个距离目标更近的位置，但是仍然不够接近，因此我们可以继续重复上述过程，最终达到一个足够接近的解。
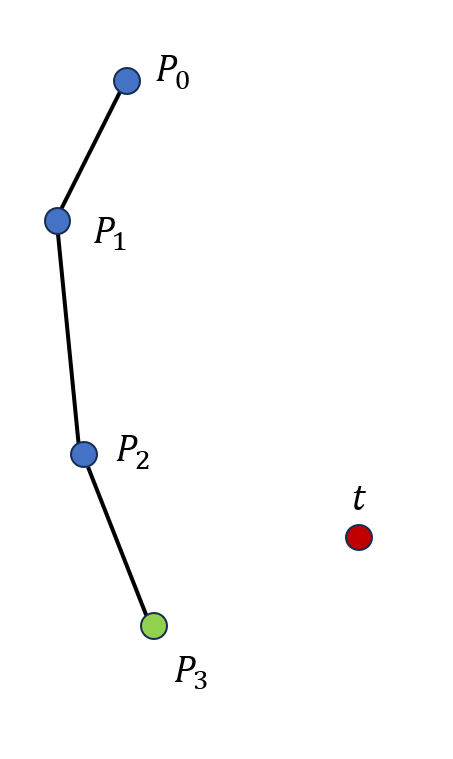(a) 初始状态
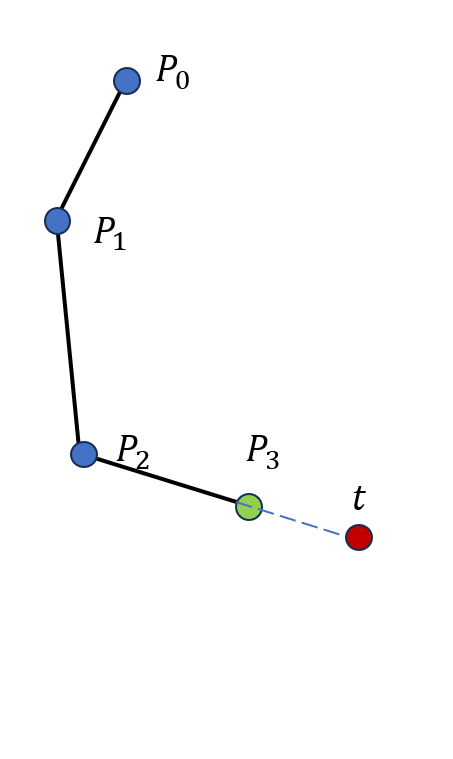(b) 第一次旋转后
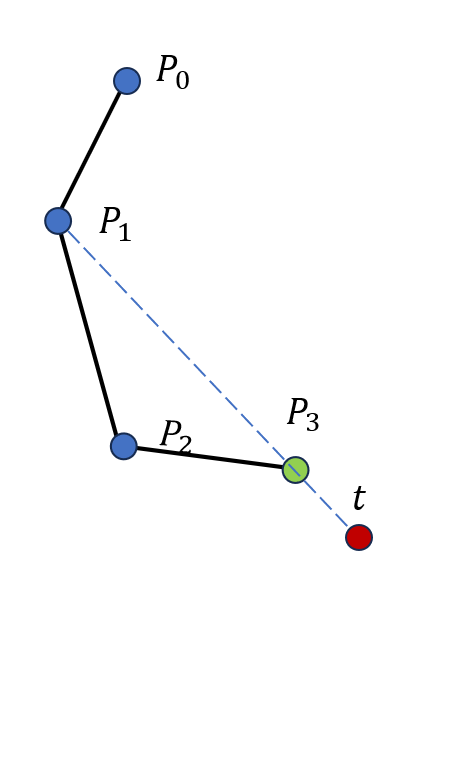(c) 第二次旋转后
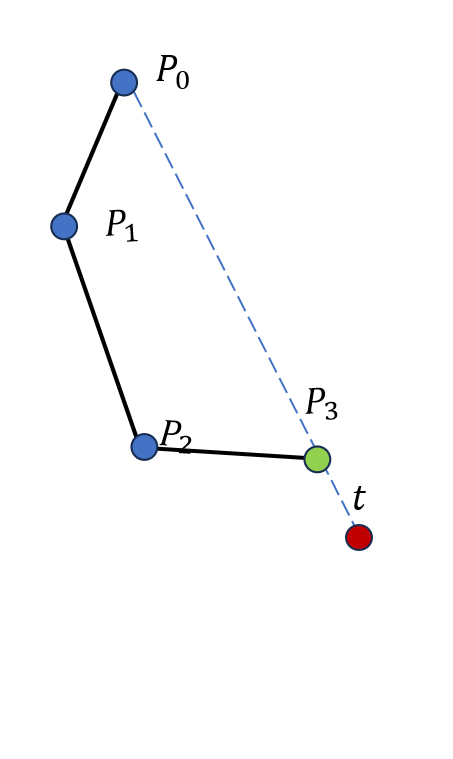(d) 第三次旋转后
图 19.17 循环坐标法求解逆向动力学的过程#
循环坐标法的优点与缺点都非常明显。其优点在于实现非常简单，进行单次迭代复杂度也较低；此外，循环坐标推演还可以很容易地扩展到包含局部约束的情形，如某些关节的旋转角度有一个特定范围。循环坐标推演也可以通过分割子链的方式，来处理更为复杂的树形关节结构。其缺点在于得到的结果的运动分布较为不自然，可能会产生大角度的旋转，导致对连续动作进行逆向运动学求解时，解的连续性较差；此外，对于精度要求较高的求解场景，其迭代效率也不够理想。
19.2.3.2. 前向和后向迭代逆运动学#
前向和后向迭代逆运动学与循环坐标法的不同之处在于它直接调整每个关节的位置，而非局部旋转，其每一轮迭代会依次进行向前迭代和向后迭代两个过程。具体地，假设每个关节在第 \(k\) 轮迭代前的位置为 \(\boldsymbol p_0^{k-1}\sim\boldsymbol p_n^{k-1}\)，向前迭代后的位置为 \(\boldsymbol p_0^\star\sim\boldsymbol p_n^\star\)，第 \(k\) 轮迭代后的位置为 \(\boldsymbol p_0^k\sim\boldsymbol p_n^k\)，我们的目标仍然是让末端位置 \(\boldsymbol p_n\) 达到目标位置 \(\boldsymbol t\)。向前迭代会从末端关节开始依次向前修改每个关节的位置，首先令 \(\boldsymbol p_n^\star=\boldsymbol t\)，随后在 \(\boldsymbol p_{n-1}^{k-1}\) 与 \(\boldsymbol p_n^\star\) 的连线上取点 \(\boldsymbol p_{n-1}^\star\) 使得向量 \(\boldsymbol p_{n-1}^\star-\boldsymbol p_n^\star\) 模长等于连接 \(n-1\) 号和 \(n\) 号关节之间的骨骼长度且方向与 \(\boldsymbol p_{n-1}^{k-1}-\boldsymbol p_n^\star\) 一致；接下来用同样的过程依次确定 \(n-2,n-3,\cdots,0\) 号节点的位置。向后迭代会从 \(0\) 号关节开始依次向后修改每个关节的位置，首先令 \(\boldsymbol p_0^k=\boldsymbol p_0^{k-1}\)，随后在 \(\boldsymbol p_1^\star\) 与 \(\boldsymbol p_0^k\) 的连线上取点 \(\boldsymbol p_1^k\) 使得向量 \(\boldsymbol p_1^k-\boldsymbol p_0^k\) 模长等于连接 \(0\) 号和 \(1\) 号关节之间的骨骼长度且方向与 \(\boldsymbol p_1^\star-\boldsymbol p_0^k\) 一致；接下来用同样的过程依次确定 \(2,3,\cdots,n\) 号节点的位置。将上述过程重复若干轮，即可逐渐逼近目标点。
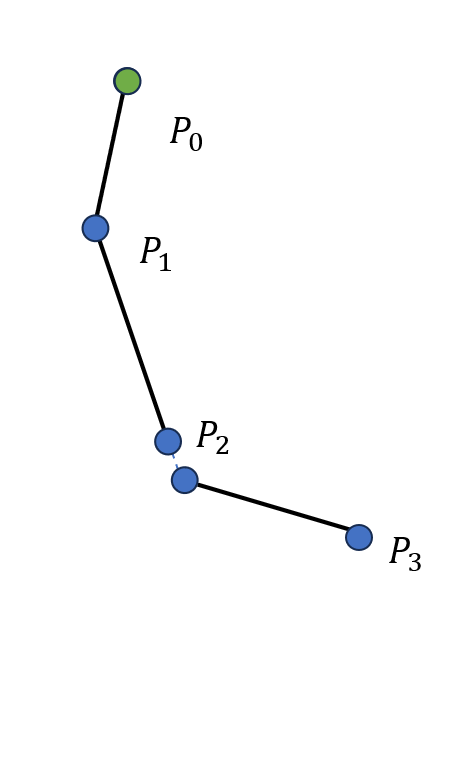
我们仍然以一个三个骨骼的系统为例，初始状态还是图 19.17(a) 所示的情形。首先是向前迭代的过程，我们将末端 \(P_3\) 移动至 \(\boldsymbol t\)，\(P_2\) 随之移动使得骨骼 \(P_3P_2\) 长度不变且指向原先 \(P_2\) 的位置，如图 19.18(a) 所示；随后移动骨骼 \(P_2P_1\) 使其与 \(P_3P_2\) 在关节 \(P_2\) 处相连，并指向原先 \(P_1\) 的位置，如图 19.18(b) 所示；接下来移动骨骼 \(P_1P_0\) 使其与 \(P_2P_1\) 在关节 \(P_1\) 处相连，并指向原先 \(P_0\) 的位置，如图 19.18(c) 所示。此后是向后迭代的过程，我们移动骨骼 \(P_0P_1\) 使得 \(P_0\) 落在初始时 \(P_0\) 的位置，并指向移动前 \(P_1\) 的位置，如图 19.18(d) 所示；接下来移动骨骼 \(P_1P_2\) 使其与 \(P_0P_1\) 在关节 \(P_1\) 处相连，并指向移动前 \(P_2\) 的位置，如图 19.18(e) 所示；然后移动骨骼 \(P_2P_3\) 使其与 \(P_1P_2\) 在关节 \(P_2\) 处相连，并指向 \(\boldsymbol t\)，如 图 19.18(f) 所示。至此，完成了一次前向和后向迭代逆运动学的完整迭代过程。
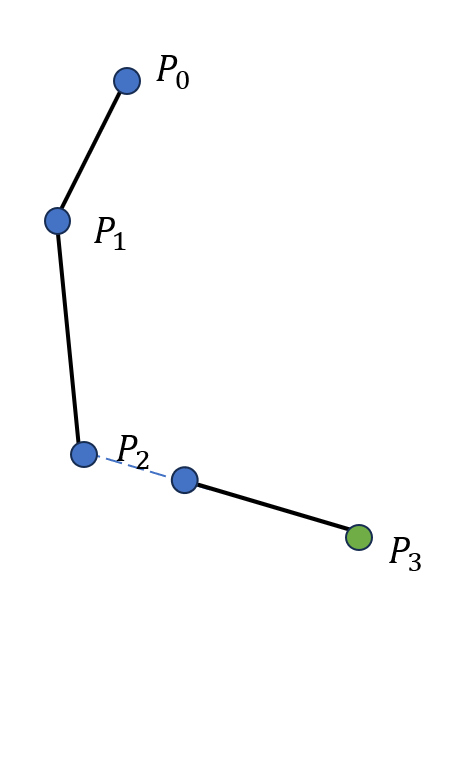(a) 第一步后
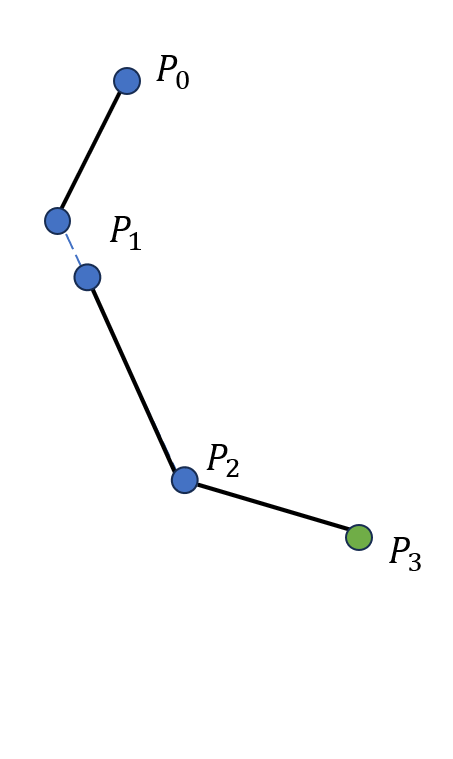(b) 第二步后
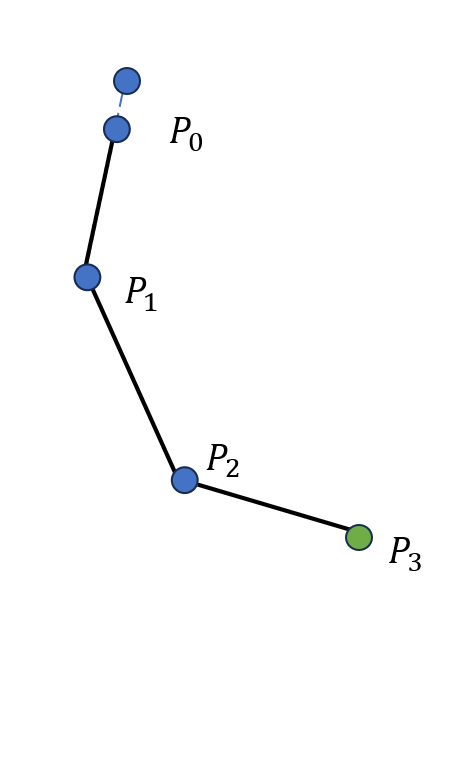(c) 第三步后
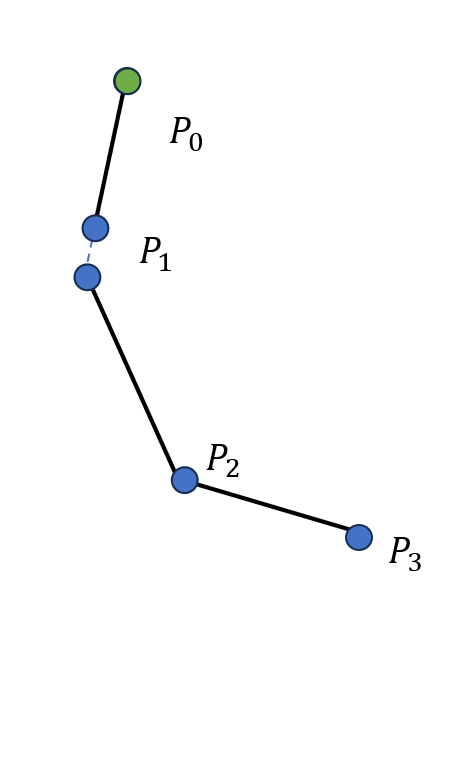(d) 第四步后
(e) 第五步后
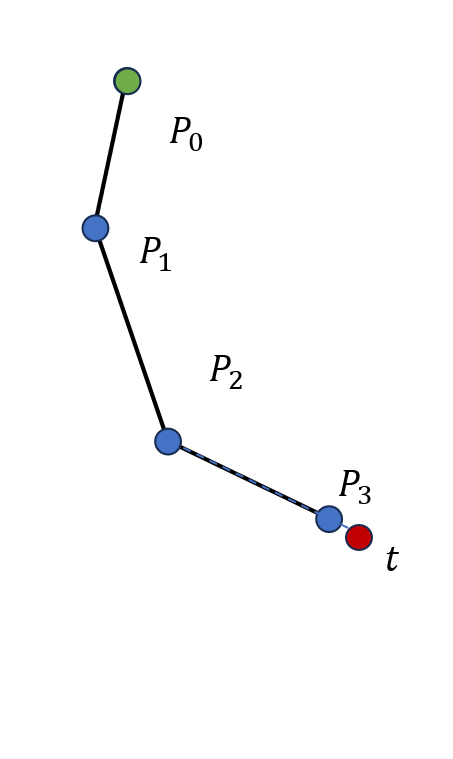(f) 第六步后
图 19.18 前向和后向迭代逆运动学的求解过程#
实践中前向和后向迭代逆运动学的收敛速度会远快于循环坐标法，对于相同的容忍度（即允许铰链刚体末端相对目标位置偏差的距离），其所需的总计算时间往往也会更少。但是对于包含关节约束的逆向运动学问题，此方法难以使用，因为关节约束往往是对旋转的约束，而此方法则是基于位置对铰链刚体进行调整。因此，前向和后向迭代逆运动学虽然高效，但应用范围有限。
19.2.3.3. 雅可比矩阵法#
逆向运动学其实本质上是一个优化问题。记所有关节上的局部旋转拼成的向量为 \(\boldsymbol\theta\)，则前向运动学的过程就是根据这些局部旋转推算出铰链刚体的末端位置，因此末端位置可以表示成这些局部旋转的函数 \(\boldsymbol f(\boldsymbol\theta)\)，再记目标位置为 \(\boldsymbol t\)，那么逆向运动学可以写成如下优化问题：
一个最简单的方式就是使用梯度下降法求解此问题，为此，我们需要求出目标函数 \(\boldsymbol F(\boldsymbol\theta)=\frac 12\Vert\boldsymbol f(\boldsymbol\theta)-\boldsymbol t\Vert^2\) 关于参数的导数：
其中 \(\boldsymbol J=\frac{\partial\boldsymbol f}{\partial\boldsymbol\theta}\) 为前向运动学的雅可比矩阵（Jacobian matrix）。因此，只要能够求出 \(\boldsymbol J\)，我们就可以使用梯度下降法优化目标函数，在每轮迭代中选取合适的正步长，为 \(\boldsymbol\theta\) 加上 \(-\alpha\nabla F\)（在此后还需要对 \(\boldsymbol\theta\) 中的每个局部旋转进行一次归一化以确保其是一个合法的旋转表示），直至目标函数降至足够低。
求 \(\boldsymbol J\) 的方法有几种。首先 \(\boldsymbol f(\boldsymbol\theta)\) 的表达式是可以写出来的（尽管十分复杂），因此我们可以直接对其关于每个关节的局部旋转的每个参数求导以算出 \(\boldsymbol J\) 的表达式。但是这种办法十分费力、容易出错，况且对于不同的铰链刚体都需要重新计算；幸运的是，我们可以借助深度学习库（如 PyTorch、TensorFlow 等）中的自动微分功能完成这件事情，这些库中往往还有许多用于训练网络的优化算法，也可以直接用来求解逆向运动学问题。此外，对于特殊的旋转表达（如欧拉角或二维情形），我们还可以使用有限差分法计算 \(\boldsymbol J\) 的近似值。例如，假设我们要计算 \(\boldsymbol J\) 的第 \(i\) 行 \(\frac{\partial\boldsymbol f}{\partial\theta_i}\)，可以取一个很小的 \(\Delta\theta_i\)，将 \(\frac{\boldsymbol f(\theta_0,\cdots,\theta_{i-1},\theta_i+\Delta\theta_i,\theta_{i+1},\cdots,\theta_n)-\boldsymbol f(\boldsymbol\theta)}{\Delta\theta_i}\) 作为近似结果。这个方法的好处是只需要进行前向运动学即可，但 \(\Delta\theta_i\) 大小的选取则需要视情况而定。