7.4. 图像抖动

图 7.26 从左到右：原图，不加抖动处理的量化，使用 Floyd-Steinberg 抖动处理后的效果[1]

抖动（dithering），是在数字信号处理领域的中一项用于降低量化误差的技术。透过在较低比特中加入噪声，借此破坏谐波的排序，使谐波的影响受到压制，并减少量化误差在低频的影响。所谓量化（quantization） 是指将连续的信号值离散化到有限值域上的过程，在图像处理中就是把连续的颜色场用计算机中有限的颜色种类尽可能接近原图地表示出来。

对于图像的量化，如果朴素地将每个像素点的颜色变成计算机中最接近的颜色种类，则会出现很不自然的颜色带，图像抖动的目的则是为了消除颜色带现象，让量化后的图片视觉上更加接近原图。图 7.26 展示了一个例子，原图是一个 RGB 三通道取值均为 0 到 255 的整数的照片 (可以近似看成连续颜色场)；如果三个颜色通道都变成只有 2 位 8 种取值，朴素的方法是直接向下取整，这样处理之后变成了中间的结果，能够看到比较明显的颜色带；采用图像抖动技术，给原图加上一些噪声之后再量化处理，就能够消除这些颜色带，在视觉上和原图更加接近。

接下来，我们将借助一个简化的任务展现各种图像抖动方法，并解释为何这样处理能够减少视觉上的误差。

7.4.1. 问题设置

我们拥有一张灰度图，其每个像素的亮度值可视为 \([0,1]\) 范围内的一个实数，现在要将其显示在一个老式显示设备上，每个像素只能取 0 或 1 的亮度值，如何才能让显示的图像在视觉上尽可能接近原图？这个问题将前文提到的例子简化成了仅有一个颜色通道的情形，并且将信号值正则化到了 0 和 1 之间的实数，以便后文的描述。这个问题有一个最朴素的解决办法：将亮度小于等于 \(0.5\) 的像素显示成黑色，否则显示成白色。这样得到的效果会像图 7.27 第二个图一样，只能看清大致轮廓，亮度的渐变效果完全丢失了，视觉上与原图相差甚远。

图 7.27 不同的图像抖动算法结果：原图，没有抖动，有序抖动，均匀随机抖动，蓝噪声随机抖动

7.4.2. 有序抖动

我们尝试着先给自己降低一点难度：假设显示器的分辨率高于图像，原图的每个像素点可以用显示器上相邻的 \(3\times 3=9\) 个像素点来显示。那么现在我们的显示器就可以显示 10 种不同的亮度了——通过调整 \(3\times 3\) 范围内白色像素点的个数来调整亮度。由此，我们可以定义一个 \(3\times 3\) 的抖动矩阵 (dithering matrix) \(M\)，\(M\) 中的所有元素构成一个 0 到 8 的整数排列，每个元素对应于显示器上 \(3\times 3\) 区域中的一个像素点，若原图相应像素的亮度值大于 \(M_{ij}/9\) (\(i,j\in\{0,1,2\}\)，下同) 则 \(3\times 3\) 区域中第 \(i\) 行第 \(j\) 列的像素点亮度设为 \(1\)，否则为 \(0\)。由此可见，\(M\) 的每个元素定义了一个亮度的阈值，将 \([0,1]\) 的亮度值拆分成了 10 个集合：\(\{0\},(0,1/9],(1/9,2/9],\cdots,(8/9,1]\)，分别对应于 10 种新的亮度。例如，取

(7.33)\[\begin{split} M=\begin{bmatrix} 6 & 8 & 4 \\ 1 & 0 & 3 \\ 5 & 2 & 7 \end{bmatrix} \end{split}\]

那么显示器上每个 \(3\times 3\) 的区域就会取图 7.28 中的几种模式。

图 7.28 当抖动矩阵按式 (7.33) 取值时，每个 \(3\times 3\) 区域可能取到的模式。注意，图中的黑点代表“亮”，白块代表“暗”，与实际显示情况相反。模式 0 对应亮度集合 \(\{0\}\)，模式 1 对应亮度集合 \((0,1/9]\)……模式 9 对应亮度集合 \((8/9,1]\)。

以上其实是借用了一种超采样的办法减少信息的丢失，如果我们要求显示器分辨率与图像一致，这个方法就不奏效了。但我们可以借助这个思路修改一下算法，得到有序抖动 (ordered dithering) 算法：将原图也划分成紧密排列的 \(3\times 3\) 的小区域，每个小区域中第 \(i\) 行第 \(j\) 列像素的亮度若大于等于 \(M_{ij}/9\) 则将其设为 1，否则设为 0。这个算法的效果如图 7.27 第三个图所示，虽然图像中出现了许多有规则的斑点，但已经能够“看出”颜色的渐变了。

你或许会怀疑，为何改进后的算法能取到比二值化更好的效果。毕竟不但没有超采样，还引入了更多的错误 (相比于直接二值化，有些亮度很高的像素反而被设成了 0，也有些亮度很低的像素反而被设成了 1)。事实上，我们可以将这个算法理解为\textbf{给整张图片加上了一个以 \(3\times 3\) 为周期的噪声}，然后再进行二值化处理。例如，考虑抖动矩阵的一个元素 \(M_{00}=6\)，当且仅当对应像素的亮度值 \(I\ge 6/9\approx 0.667\) 时才设为 \(1\)，这等价于当 \(I-0.167\ge 0.5\) 时将 \(I\) 设为 1，也就是给 \(I\) 这个像素点加上了 \(-0.167\) 的扰动之后再进行二值化。至于为何加上噪声之后再二值化会得到更好的效果，我们会在下一节解释。

7.4.3. 基于噪声的抖动

借助前文的思想，我们可以将加上的噪声换成另外一些随机生成的噪声，就得到了基于噪声的抖动 (dithering with noise)。

7.4.3.1. 噪声的作用

我们首先考虑一个具体的例子：假如我们的原图所有像素的亮度值均为 0.3。记图片的像素个数为 \(N\)，定义量化后图片与原始图片的平均误差 \(E\) 如下：

(7.34)\[ E=\frac 1N\sum_{i=0}^{N-1}f_i-g_i \]

其中 \(f_i\) 表示原图第 \(i\) 个像素的亮度，\(g_i\) 表示量化后的像素亮度。

如果直接以 0.5 作为阈值进行二值化，所有像素的亮度都会被截断成 0，平均误差 \(E_\text{truncate}=0.3\)。如果我们对原始图片的每个像素点都加上一个在 \([-0.5,0.5]\) 中均匀取值的随机干扰，然后再以 0.5 为阈值进行二值化，此时平均误差 \(E_{\text{noise}}\) 会变成一个随机变量：

(7.35)\[ E_\text{noise}=\frac 1N\sum_{i=0}^{N-1} 0.3-I_{\{0.3+\epsilon_i>0.5\}} \]

其中 \(I_A\) 称为事件 \(A\) 的示性函数，当 \(A\) 发生时取 1，否则取 0；\(\epsilon_i\) 即为加给像素 \(i\) 的随机扰动。由于这里 \(E_\text{noise}\) 变成了一个随机变量，我们分析它的期望才有意义：

(7.36)\[\begin{split} \begin{aligned} \mathbb E[E_\text{noise}]&=\frac 1N\sum_{i=0}^{N-1}0.3-\mathbb E[I_{\{0.3+\epsilon_i>0.5\}}]\\ &=\frac 1N\sum_{i=0}^{N-1}0.3-P(0.3+\epsilon_i>0.5)\\ &=\frac 1N\sum_{i=0}^{N-1}0.3-P(\epsilon_i>0.2)\\ &=0 \end{aligned} \end{split}\]

其中，\(P(A)\) 表示事件 \(A\) 发生的概率。我们惊奇地发现，在期望意义下误差变成了 0。虽然噪声的引入让部分像素点与原始图片的差别更大，但在平均意义下误差变小了，这也是为什么从“整体”上来看，加入噪声反而让量化效果更好。

7.4.3.2. 白噪声与蓝噪声

事实上，上述加噪声的方法又被称为白噪声抖动算法 (white noise dithering)。这个方法的效果如图 7.27 第四个图所示，相比于直接二值化，这个结果能看出灰度的渐变，但总体效果不如有序抖动方法，我们会感觉图片的噪声十分“刺眼”。通过改变噪声的种类，我们可以用蓝噪声抖动算法 (blue noise dithering) 对图像进行量化，效果如图 7.27 第五个图所示。这个结果不仅能看出灰度的渐变，而且相比白噪声抖动而言，我们对图片上噪声的感觉没有那么明显。

为什么白噪声与蓝噪声会产生如此不同的效果呢？我们对两个图中加的扰动分别进行傅里叶变换，得到的能量频谱频谱如图 7.29 所示。不难观察到，白噪声的能量在各个频率上接近均匀分布，而蓝噪声的能量则主要集中在高频部分，事实上，这正是白噪声和蓝噪声的定义。

图 7.29 干扰信号经过傅里叶变换后的结果：左图为白噪声，右图为蓝噪声

人类的眼睛对低频信号较为敏感，高频信号则更难被察觉。我们能够明显地察觉到白噪声，但却很难发现蓝噪声的存在，这就是为何蓝噪声抖动的效果要远远好过白噪声抖动。事实上，人眼视网膜细胞的位置分布类似于蓝噪声分布，因此能够用有限的细胞数量呈现高分辨率。如图 7.30 所示，在采样点数目相同的情况下，蓝噪声采样会比白噪声采样看上去更接近原图。蓝噪声在计算机图形学中还有着广泛的应用，如物理模拟、渲染、几何处理等几乎所有涉及到采样的任务。如何生成蓝噪声也是一个十分值得研究的课题，这方面可以参考彭罗斯瓷砖 (Penrose tiling)、王浩瓷砖 (Wang tiling) 等方法。

图 7.30 蓝噪声采样与白噪声采样

7.4.4. 基于误差扩散的抖动

图像抖动还有一种基于误差扩散的算法 (dithering with Error diffusion)，叫做弗洛伊德-斯坦伯格抖动算法 (Floyd-Steinberg Dithering)，它的思想是将单个像素的量化误差传递到其他像素，从而保证总误差接近于 0。

弗洛伊德-斯坦伯格抖动算法的流程是：从左到右、从上到下依次处理每一个像素点，将当前像素点的亮度以 0.5 为阈值进行二值化，将二值化前的亮度减去二值化后的亮度作为误差值，然后将误差值分成占比分别为 \(7/16, 3/16, 5/16, 1/16\) 的四个部分，并分别加到右方、左下方、下方、右下方四个像素的亮度值，已处理好的像素点不受影响[1]。如图 7.31 所示，黑点所在的方格为当前处理的像素点，灰色方格表示已处理的像素点，白色方格表示未处理的像素点。

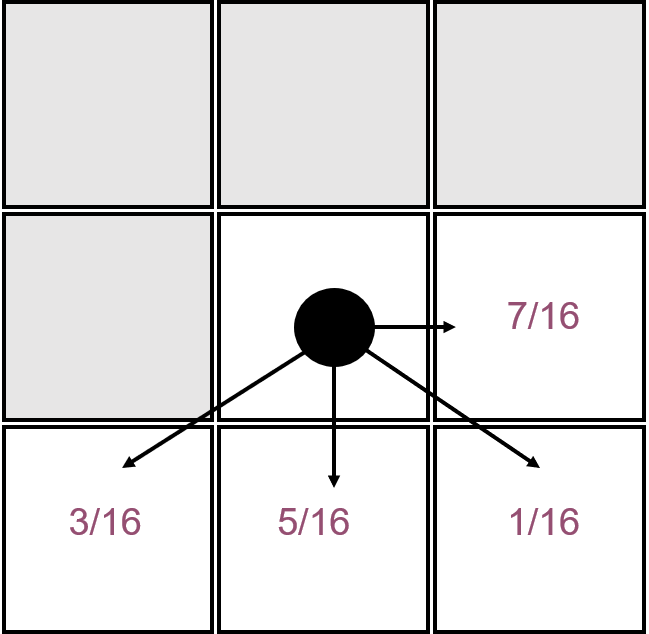
图 7.31 弗洛伊德-斯坦伯格抖动算法的误差扩散过程

这是一个确定性的算法，效果如图 7.32 所示，它的效果与蓝噪声抖动相当，同时又不会出现有序抖动的规则性斑点。但是由于它需要不断地扩散误差，所以它的计算速度 会更慢。

图 7.32 弗洛伊德-斯坦伯格抖动算法效果

---

[1] (1,2)

Wikipedia: Floyd–Steinberg dithering