标量场、矢量场、张量场数据的可视化

25.1. 标量场、矢量场、张量场数据的可视化#

在科学计算与工程分析中，不同的物理量常以不同的数学形式存在，例如温度、电势等标量，速度、力等矢量，以及应力张量等更复杂的量。为了清晰有效地展示这些量的空间分布与变化趋势，我们需要根据物理量的类型，采用具有针对性的可视化策略。

25.1.1. 按物理量性质分类：标量场、矢量场、张量场#

25.1.1.1. 标量场数据#

标量场（Scalar Fields）数据是单值分布在空间网格上的数据，每个空间点对应一个标量值。 常见的标量场数据有：医学影像（CT 扫描的 Hounsfield 单位值），气象数据（全球温度分布、大气压强）等。

25.1.1.2. 矢量场数据#

矢量场（Vector Fields）数据在空间每个点上具有方向与大小，通常表示为三维向量。 常见的矢量场数据有：流体力学（流速场、压力梯度场），电磁学（电场强度、磁场方向），气象学（风向与风速场）。

25.1.1.3. 张量场数据#

张量场（Tensor Fields）数据在空间每个点上为二阶张量（如 3×3 矩阵），常用于描述各向异性现象。 常见的张量场数据有：材料科学（应力张量、应变率张量），医学成像（扩散张量成像），地质学（岩石渗透率张量）。 张量场数据具有方向各向异性和高维复杂性，可视化中需要努力克服信息过载及交互分析能力不足的问题。

25.1.2. 标量场可视化#

标量可视化是将分布在空间中的标量值数据转换为人类可感知的视觉形式（如颜色、线条等）的过程，以下我们将介绍几种经典方法。

25.1.2.1. 颜色映射#

颜色映射（Color Mapping）是一种常见的标量可视化技术。其原理是把标量数据的数值，按照一定的规则，映射到颜色空间（如 RGB 或 HSV）里的颜色，这样每个数值就有了一个直观可见的“颜色表达”，颜色差异代表了数值差异。

颜色映射的基本定义式如下：设 \(S\) 为定义在域 \(D\) 上的标量场，\(S:D \rightarrow \mathbb{R}\) ，其中 \(D\subseteq \mathbb{R}^2\)，那么对域 \(D\) 内的任意点 \(\boldsymbol{x} \in D\)，它映射到的颜色值可以写为

(25.1)#\[ V(\boldsymbol{x}) = T(S(\boldsymbol{x}))， \]

\(T\) 表示颜色映射函数，可以定义为：

(25.2)#\[ T: [S_{\text{min}}, S_{\text{max}}] \rightarrow C， \]

其中 \([S_{\text{min}}, S_{\text{max}}]\) 是 \(S\) 的值域，\(C\) 表示颜色空间。 最终，对于所有 \(\boldsymbol{x} \in D\)，都可以将 \(\boldsymbol{x}\) 在域 \(D\) 中的标量值 \(S(\boldsymbol{x})\) 通过颜色映射函数 \(T\) 转换为一个颜色，从而实现可视化。

颜色映射函数 \(T\) 的定义方式是多种多样的，基于色标来定义颜色映射函数是一种最直接的方案，如图 25.2，其流程包含如下步骤：

  1. 数据归一化：原始的标量场数据可能取值范围很大，且核心数据集中分布在更小的区间（如气温等），因此首先需要选定想要考察的标量值范围 \([\bar{S}_{\text{min}}, \bar{S}_{\text{max}}]\)，将 \(S\) 缩放到标准范围 \([0,1]\) 内（这里我们采用了线性的放缩，如果想突出某些特定数值区域，还可以用非线性归一化，比如对数、指数映射），并将超出考察范围的值截断至边界：

(25.3)#\[\begin{split} \bar{S} = \begin{cases} 0, & S < \bar{S}_{\text{min}} \\ 1, & S > \bar{S}_{\text{max}} \\ \frac{S - \bar{S}_{\text{min}}} {\bar{S}_{\text{max}}-\bar{S}_{\text{min}}}, & \text{otherwise} \end{cases} \end{split}\]

  1. 定义色标：色标也被称为颜色查找表（colormap），它本质上是定义了从 \([0,1]\) 区间到颜色空间的连续映射函数。Matplotlib、Matlab 等工具中包含了多种预定好的色标方案，包括 Jet、Viridis 等，如图 25.1 所示。也可以进行色标的自定义，如：先定义 \([0,1]\) 内若干离散值对应的具体颜色，而后通过插值方法（§6）得到连续的颜色映射方案。

  2. 查找颜色：用归一化后的标量值 \(\bar{S}\) 作为索引，从色标中取出对应的颜色。

../../_images/visualization-scientific-colormap.png

图 25.1 根据不同可视化目标预定义出的色标。© Matplotlib#

颜色映射方法简单直接，且不占用位置、形状等视觉映射通道，因此被广泛用于各类数据的可视化，如二维平面数据、三维表面数据、体积数据等等，如图 25.2 所示。

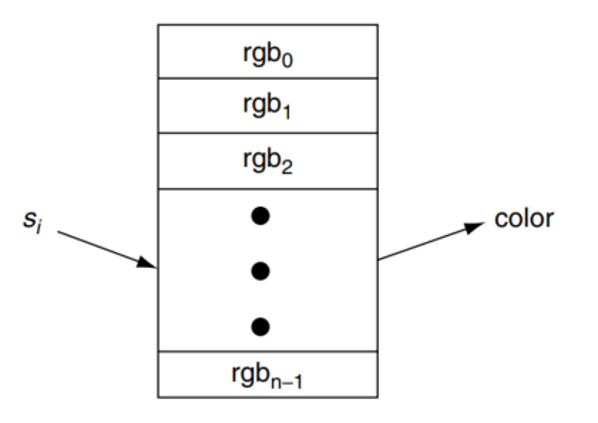
../../_images/visualization-scientific-color_mapping.png

图 25.2 不同类型数据的颜色映射。左：二维泰勒涡的流速场大小可视化 [PGW24]；中：三维空间中磁感线上磁感应强度大小可视化 [SNZ+21]；右：汽车撞击时所受应力大小在汽车模型表面的可视化 © Wikipedia。#

25.1.2.2. 等值线与等值面#

颜色映射的一个自然扩展是等值线（contours）的绘制。 当我们看到一个用数据值着色的表面时，眼睛常常将颜色差别较大的相近区域区分为不同的区域。 当我们绘制等值线时，实际上就是在构造这些区域之间的边界。 对于选取的某个标量值 \(c\)，等值线 \(S(\boldsymbol{x})=c\) 就是划定两个区域 \(S(\boldsymbol{x}) < c\) 和 \(S(\boldsymbol{x}) > c\) 之间分割线。等值线在地理学、气象学等自然领域有着重要应用，地图上的等高线、气温分布图上的等温线就是等值线的具体应用。

基于等值线的可视化就是将标量场中数值相同的点用线条连接起来，从而直观展现标量场的走势。在给定了需要生成的等值线的值后，由于实际数据多为离散采样点，绘制等值线需要经过定位离散等值点和插值得到线条两步。

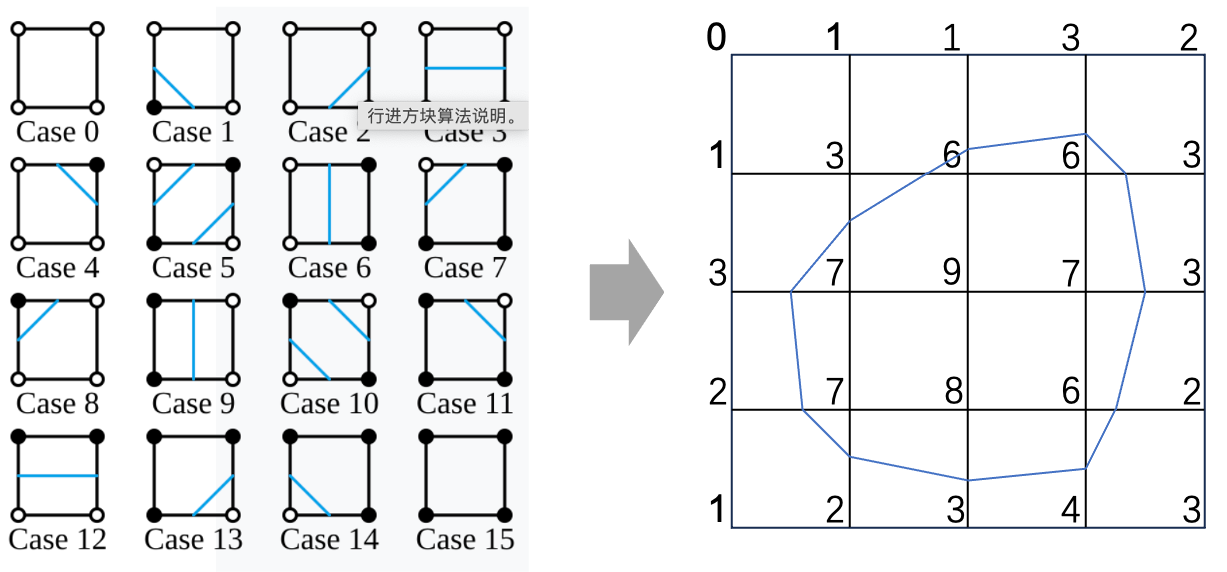
../../_images/visualization-scientific-contour.png

图 25.3 左：行进方块算法连线方案 © Wikipedia；右：一个简单的等值线（\(c=5\)）测绘示意图。#

一个简单的实例如图 25.3 右所示，考虑图中的 2D 结构化网格（数字代表网格点处的标量值）中 \(c=5\) 的等值线绘制。首先，由于等值线值可能位于离散的格点之间，我们首先需要在各条边上找到对应的等值点，由于最常见的插值技术是线性插值，因此这里也可以根据线性关系进行定位：若某条边的两个顶点 \(\boldsymbol{x}_1,\boldsymbol{x}_2\) 处的值 \(S_1, S_2\) 跨越了值 \(c\)，即 \(S_1\le c\le S_2\)，那么可以认为这条边上存在一个等值点

(25.4)#\[ \boldsymbol{p} = \boldsymbol{x}_1 + \frac{c-S_1}{S_2-S_1} \cdot (\boldsymbol{x}_2-\boldsymbol{x}_1)。 \]

例如，如果一条边在其两个端点的标量值为 10 和 0，并且我们试图生成值为 5 的等值线，则计算可知等值线通过这条边的中点。

确定离散的等值点之后，我们需要把这些点连接起来，形成完整的等值线。由于等值线是局部连续的，也只受到局部数值的影响，因此，我们可以采用分而治之的策略，认为每个单元格内部的处理是互不影响的，一个单元格内的四个顶点及其数值，已经完全决定了：等值线要不要经过这个单元格；以及，如果经过，应该从哪个边进，从哪个边出。 而在每个单元格内，由于每个顶点只有“内部”或“外部”两种状态，因此格点的状态组合只有 \(2^4=16\) 种可能，因此等值线在每个单元格内部的走法是有限且可以分类的，如图 25.3 左所示。因此，只要根据单元格状态选择对应的连线方案，就可以得到最终连接好的等值线。这一方案被称为 “行进方块算法”（Marching Squares）。

一个 2D 温度场的等值线（等温线）绘制结果如图 25.4 所示。

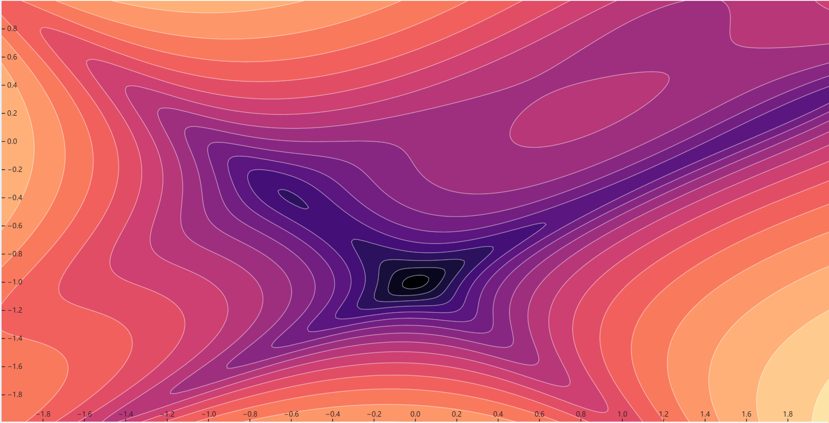
../../_images/visualization-scientific-temperature.png

图 25.4 2D 温度场的等温线可视化。#

思考

在图 25.3 中，我们根据16种单元格状态分类用线段连接了所有边上的等值点。如果要绘制出如图 25.4 中圆滑的等值曲线，有没有更好的连接方案呢？

等值线扩展到三维空间内的版本就是等值面（isosurface），它能够揭示出数据中具有特定意义的内部结构，比如医学图像中的器官轮廓、流体中的温度分布边界等。等值面绘制是三维标量场可视化中的核心技术之一。

等值面绘制的经典算法是“行进方块算法”的三维版本——“行进立方体算法”（Marching Cubes）。这一算法也常被用于体数据的表面重建任务（如：流体、符号距离场的表面重建）。其算法思想与前者类似，区别在于每个单元从二维变成了三维。对于三维数据，考虑到立方体单元格中有八个点，因此每个单元格有 \(2^8=256\) 种标量值组合的可能。但是由于旋转平移对称性可以进一步缩减案例中的数目，一个经典的版本如图 25.5 所示。关于行进立方体算法的算法流程可以参考威廉·洛伦森 （William Lorensen）等人的工作 [LC98]。

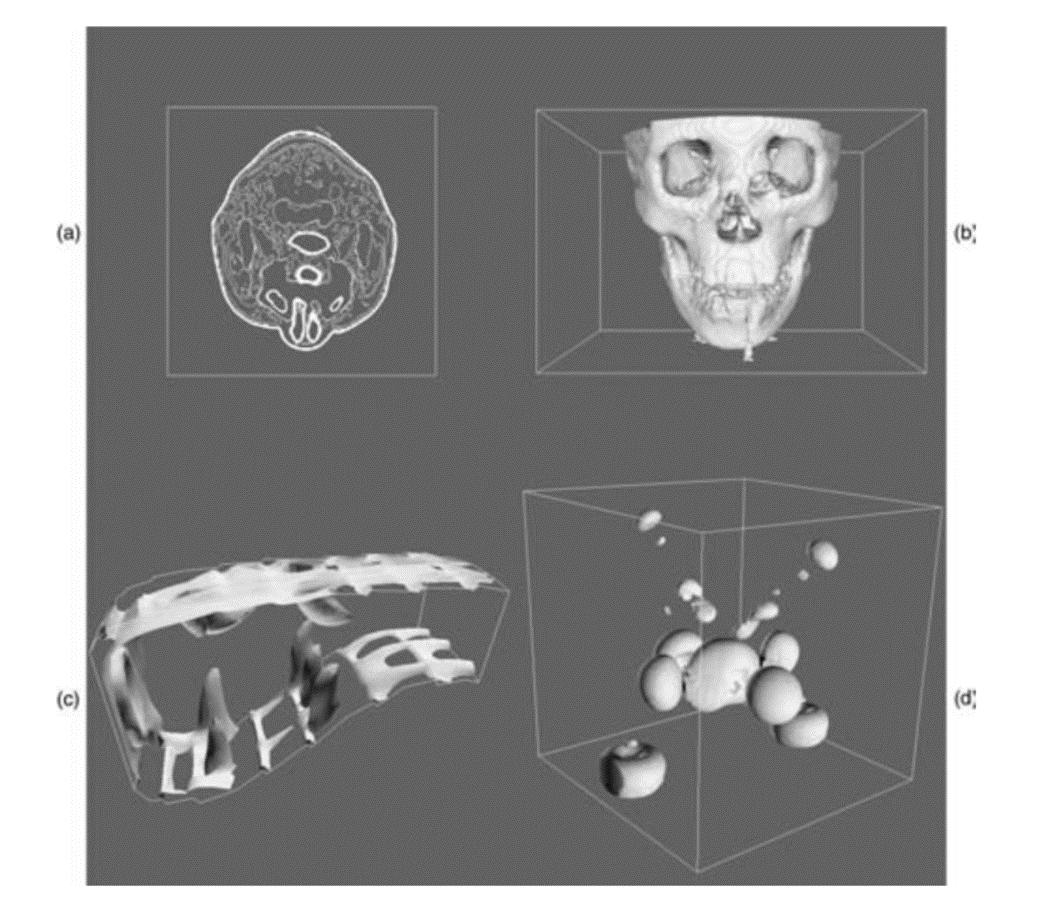
../../_images/visualization-scientific-marching_cubes.png

图 25.5 行进立方体算法的等值面绘制方案（最初发布的15种构型的版本）。 © Wikipedia#

图 25.6给出了一些利用Marching Cubes算法进行重建的结果。

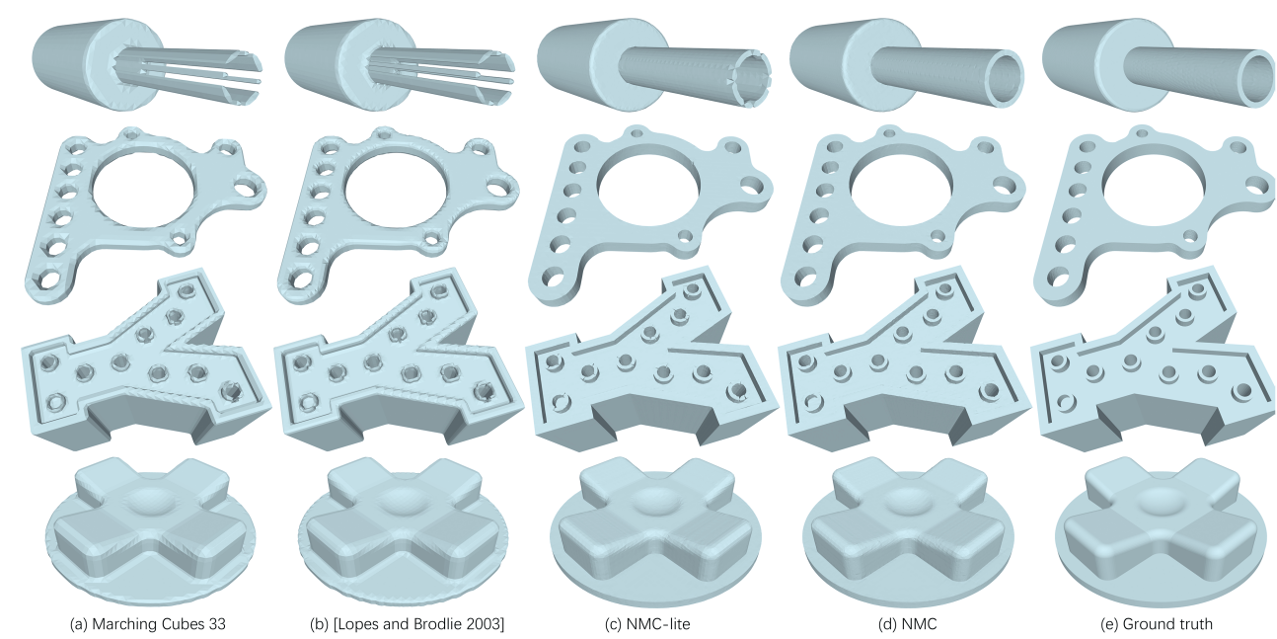
../../_images/visualization-scientific-marching_cubes_results.png

图 25.6 不同版本的行进立方体算法的一些结果。[CZ21]#

25.1.3. 矢量场可视化#

矢量场可视化通过图形化手段表达矢量数据的方向、大小及动态特性，是流体力学、气象学、电磁学等领域的核心分析工具。

25.1.3.1. 箭头表示法#

对于矢量场的可视化，使用箭头（arrows）来表示某点处的矢量是一种最简单直接的方式，中学物理课中的箭头标注的受力分析图就是使用箭头表示矢量的一个范例。

设 \(\boldsymbol{v} \) 为定义在域 \(D\) 上的矢量场，其中 \(\boldsymbol{v}: D \rightarrow \mathbb{R}^n\)（通常 \(n\) = 2 或 3 ），表示每个点 \(\boldsymbol{x} \in D\) 的矢量值。 箭头表示法在矢量场的定义域上采样一组点（通常是网格点），并在每个点上绘制一个箭头（也叫向量图元或 glyph），该箭头的方向对应矢量方向，箭头大小（按一定的缩放比例）对应矢量大小。 但需要注意的是，这个缩放比例只用于将“矢量大小”转换成“箭头长度”的可视比例，是将矢量的数值大小映射到可视化中所用的一种尺度表示，并不等同于场景的真实空间尺度。

  • 方向： 在点 \(x\) 处的箭头方向与矢量 \(\boldsymbol{v}(\boldsymbol{x})\) 方向一致。可以用矢量的单位向量 \(\hat{\boldsymbol{v}}(\boldsymbol{x}) = \frac{\boldsymbol{v}(\boldsymbol{x})}{\|\boldsymbol{v}(\boldsymbol{x})\|}\) 表示，其中 \(\|\boldsymbol{v}(x)\|\) 是矢量的大小（模长）。

  • 长度： 箭头的长度通常与矢量的大小成比例。可以定义为 \(L(x) = k \cdot \|\boldsymbol{v}(\boldsymbol{x})\|\)，其中 \(k\) 是缩放因子。

最终，矢量场的可视化 \(\boldsymbol{v}\) 可以表示为一组箭头，其中每个箭头的位置、方向和长度由 \(\boldsymbol{x}\)、\(\hat{\boldsymbol{v}}(\boldsymbol{x})\) 和 \(L(\boldsymbol{x})\) 决定。这可以表示为 \((\text{位置: } \boldsymbol{x}, \text{方向: } \hat{\boldsymbol{v}}(\boldsymbol{x}), \text{长度: } L(\boldsymbol{x}))\)。

图 25.7 图展示了箭头表示法的效果图。左侧图是一个标准的箭头图；中间图改用了水滴形状的箭头，并改用颜色而非箭头长度来表示矢量场大小，这是一种与颜色映射方法的结合；右侧图展示了一个定义在二维空间上的三维矢量场的可视化，使用三维的红色圆箭头表示矢量，并且使用了 3D 渲染技术以获得真实的可视化效果。

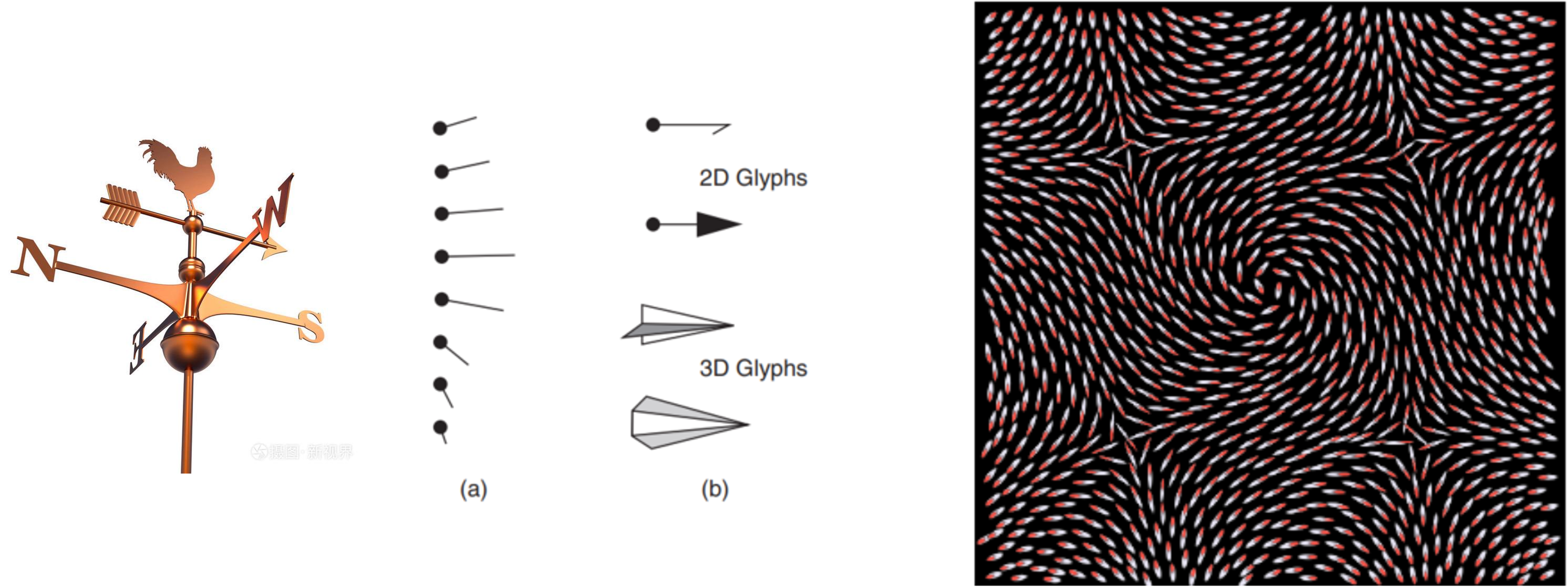
../../_images/visualization-scientific-vector_field.png

图 25.7 箭头表示法示例。左：标准的箭头可视化 © Wikipedia；中：使用水滴形箭头的可视化 © Wolfram；右：三维箭头的可视化（薄壳材料的剩磁强度分布）[CNZ+22]。#

25.1.3.2. 流线，路径线，迹线#

在矢量场可视化中，流场（例如空气流动、水流等）可视化是其中最常见且直观的重要应用，许多矢量场可视化技术最初就是为流场设计的。流场可视化用于研究和理解复杂的三维涡流动和湍流的物理过程。这些流动可能是稳定的或非稳定的，流动模式也可以以多种方式显示，如染料或烟雾注入流场后拍摄的照片，或是使用一些技术（如热线或数字粒子图像测速法）测量的矢量场。为了更系统地分析流动特性，人们通常会从测量数据中提取流线、迹线或路径线等辅助图形，用以揭示流体的局部行为和整体演变。

1. 流线（streamlines）

流线是相对静止（稳态）或瞬时切片情况下，通过一个种子点在空间中连续积分速度向量得到的空间曲线。流线关注的是瞬时流场的结构，在非稳定流场中流线的形态会随时间变化。这里积分所使用的速度向量是在特定时刻的流场中各点的流速矢量。换言之，流线展示了“如果在特定时刻将粒子置于某点，它的瞬时流动方向轨迹”（如图 25.8），但并不是一条真实的运动轨迹，不应用于展示流体随时间的实际运动路径。

设流场在时刻 \(t_0\) 的速度场为 \(\boldsymbol{v}(\boldsymbol{x}, t_0)\)。 引入一个积分参数 \(s\)，流线 \(\boldsymbol{x}(s)\) 可以定义为：

(25.5)#\[\begin{split} \frac{d\boldsymbol{x}(s)}{ds} &= \boldsymbol{v}(\boldsymbol{x}(s), t_0), \\ \boldsymbol{x}(0) &= \boldsymbol{x}_0. \end{split}\]

其中：

  • \( \boldsymbol{x}_0\) 是流线上一个起始点；

  • \(s\) 可以理解为沿曲线的“积分步”或“路径长度”参量；

  • \(\boldsymbol{v}(\boldsymbol{x}(s), t_0)\) 表示在时刻 \(t_0\) 位置 \(\boldsymbol{x}(s)\) 的速度向量。

流线的计算流程：

  1. 选取种子点：可手动或自动选择若干点作为粒子的初始位置；

  2. 数值积分：在向量场中，以初值 \(\boldsymbol{x}_0\) 为起点，通过积分方法（如欧拉方法或龙格-库塔方法， 前者是一阶近似，计算快但精度低；后者有四阶精度，稳定性高，广泛应用于工程仿真）不断更新粒子位置；

  3. 停止条件：达到网格边界、速度阈值过小或最大积分步数后终止。

  4. 将积分得到的点序列连成曲线，并对曲线进行着色(如速度大小)或其它视觉编码。

也可以通过一些实验的方法观测流线。由于流线只有在很短的时间内才可以认为是恒定的，于是实验上观测流线的方法是，观察摄入染料的短时间内（曝光时间量级）线形。

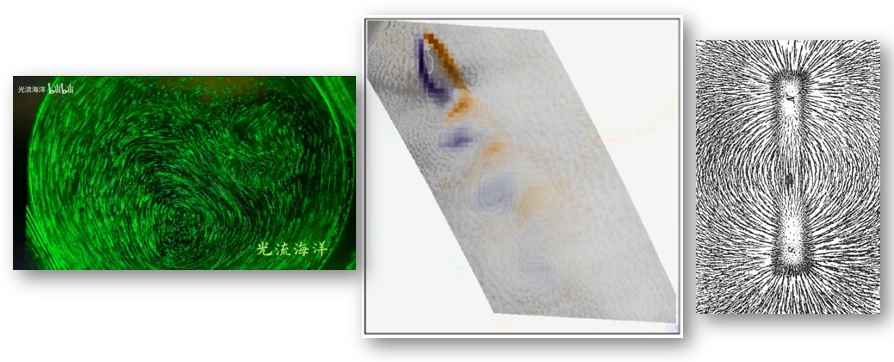
../../_images/visualization-scientific-streamline.png

图 25.8 流线示例。左：与箭头表示法结合的流线绘制；中：条形磁铁周围的磁力线，由撒在磁铁上方纸上的铁屑排列表示；右：世界地图上的洋流示意。 © Wikipedia#

对于时变流场，则可以选择路径线和迹线来展示随时间变化的流动。

2. 路径线（pathlines）

与流线不同，路径线在非稳态流场（随时间变化的场）中表示从开始点到结束点的实际运动轨迹。它反映了粒子在真实时间维度下的移动过程。 因此，在稳态流场中，各处流速不随时间变化，路径线与流线重合，但在非稳态流场中，路径线与流线不再等价。

对于一个在时刻 \(t_0\) 处于位置 \(\boldsymbol{x}_0\) 的粒子，将其随时间 \(t\) 变化的轨迹记为 \(\boldsymbol{x}(t)\)，则满足：

(25.6)#\[\begin{split} \frac{d\boldsymbol{x}(t)}{dt} &= \boldsymbol{v}(\boldsymbol{x}(t),t),\\ \boldsymbol{x}(t_0) &= \boldsymbol{x}_0. \end{split}\]

其中：

  • \(\boldsymbol{v}(\boldsymbol{x},t)\) 是非稳态（或稳态）流场随时间变化的速度函数；

  • \(\boldsymbol{x}(t)\) 称为路径线或粒子轨迹。

路径线计算流程：

  1. 时序数据获取：流场在多个时间步(如 \(t_0\)，\(t_1\)，\(t_2\)，…)上都有速度向量信息；

  2. 积分方法：在每个时间步以粒子当前位置为初值，积分到下一时间步时的粒子位置；

  3. 连接轨迹：将所有时间步粒子的空间位置连成曲线。

路径线可以通过跟踪射入的粒子的长程轨迹来实验得到。 如下面的实验图。

../../_images/visualization-scientific-pathline.png

图 25.9 路径线示例：长时间曝光的篝火火花照片显示了热空气流动的路径。© Wikipedia#

3. 迹线（streaklines）

用来表示在同一空间位置持续释放的粒子所形成的轨迹。直观地说，想象不断地往水流中滴墨水，那么这些墨滴在流体中被带动形成的一条连续曲线，就是迹线。迹线描述的事连续注入的粒子的集合运动，而不是依赖某个粒子的历史轨迹。迹线在实验流体动力学中常用，比如通过注入染料或烟雾来观察流动。

设:

  • \(\boldsymbol{v}(\boldsymbol{x},t) \)为流场的速度场（向量场）；

  • 在坐标 \(\boldsymbol{x}_0\) 处持续释放粒子；

  • \(\tau\) 表示粒子的释放时刻（可从 0 到当前时刻 \(t\) 范围内）。

对于在时间 \(\tau\) 被释放的粒子，我们用 \(\boldsymbol{x}(t;\tau)\) 表示它在时间 \(t\ge\tau\) 时所处的位置，满足以下常微分方程：

(25.7)#\[\begin{split} \frac{d\boldsymbol{x}(t;\tau)}{dt} = \boldsymbol{v}(\boldsymbol{x}(t;\tau),t),\\ \end{split}\]

并且它的初值条件（初始位置）为:

\[ \boldsymbol{x}(\tau;\tau) = \boldsymbol{x}_0. \]

即该粒子在被释放的瞬间（\(t=\tau\)）在 \(\boldsymbol{x}_0\) 位置。

../../_images/visualization-scientific-streakline.png

图 25.10 迹线示例。左：风洞中汽车周边的空气流动 © Wikipedia；右：模拟软件中飞机周边的空气流动 © Paraview。#

总结来说，流线、路径线、迹线可视化在流体动力学、气象学和海洋学等领域中非常有用，它们帮助揭示流体流动的模式和结构。三者均是理解流体运动特征、构建流体可视化的重要工具。在非稳定流动中，迹线和流线、路径线会有明显的差异，而在稳定流动中，三者会重合。 在具体应用时，应根据是否稳态、对粒子演化的关注程度以及实验/模拟中注入位置等因素，选用或结合使用这几种曲线形式来进行分析与展示。

25.1.3.3. 点噪声法#

点噪声法（spot noise）属于基于纹理的矢量场可视化技术，通过在图像平面上铺设许多“微型噪声点（spots 或 dots）”，并且让这些小斑点的形状、方向、拉伸程度等与局部向量信息相对应，从而在整体上形成密集且连续的流动纹理效果。

点噪声法的核心原理：

  1. 采样噪声点：在矢量场定义域内随机采样噪声点（比如采样每个像素点）；

  2. 局部变形：在每个噪声点处放置一个扩散核，根据该位置上的矢量方向 \(\boldsymbol{v}(x,y)\) 调整点扩散核的形变（例如：让其朝流向方向拉伸）；

  3. 叠加与渲染：将所有点扩散核以一定的密度投影或累加到最终图像中，形成一张连续纹理，会呈现出矢量场的流动趋势、局部结构甚至涡旋。 可以使用一个简单的线性组合来完成叠加 [dLvL98]：

(25.8)#\[ I(\boldsymbol{x}) = I_0 + \sum_i\alpha_i \cdot h(\boldsymbol{x}-\boldsymbol{x}_i) \]

其中，\(I(\boldsymbol{x})\) 是最终图像的强度，\(I_0\) 是可以额外设置的背景强度，\(\alpha_i\) 是每个扩散核调节因子，用来控制噪声对最终图像的影响程度，\(h\) 被称为点函数（spot function），用于表达形变后的扩散核，是一种形状核函数（类似于一个局部纹理模板），可以有不同的设计方案。

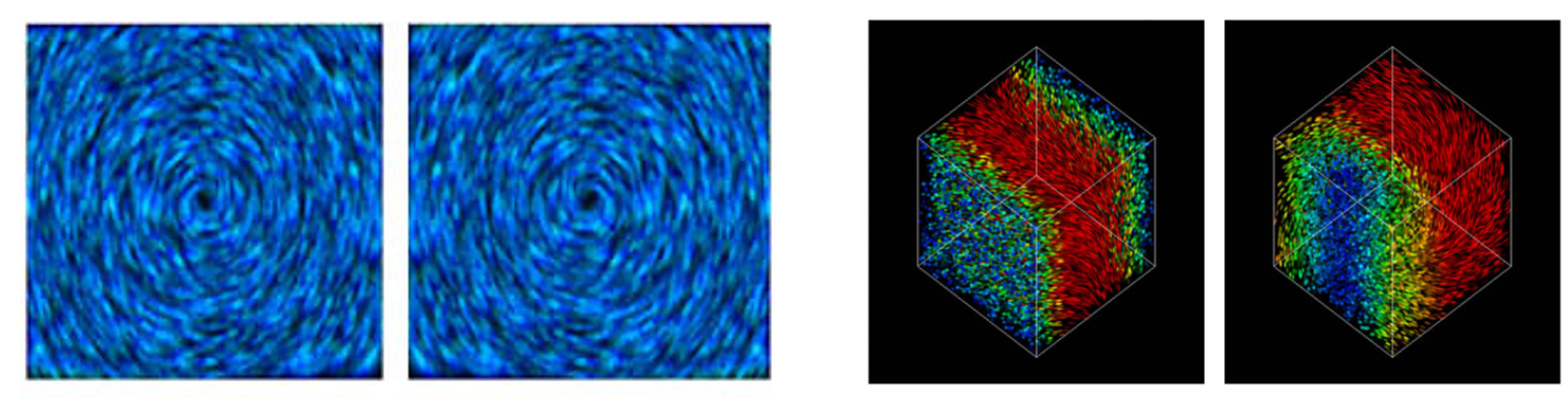
../../_images/visualization-scientific-spot_noise_2D%263D.png

图 25.11 基于点噪声法可视化 2D（左）、3D（右）矢量场，颜色对应矢量大小。[Sab02]#

点噪声法算法的优点在于它能生成直观流场可视化图像，缺点是在处理非常高速或高度湍流的流场时，可能无法清晰展示所有细节。

25.1.3.4. 线性积分卷积#

线性积分卷积（Line Integral Convolution，LIC）是一种具有 2D/3D 矢量场通用性的新技术，如图 25.12 所示，能够成像密集矢量场、独立于预定义的纹理生成稠密可视化效果，并且可以应用于二维和三维数据中。

../../_images/visualization-scientific-lic_examples.png

图 25.12 LIC 方法示例。[CL93] 左：北美风速场；右：速度归一化后的流场示例。#

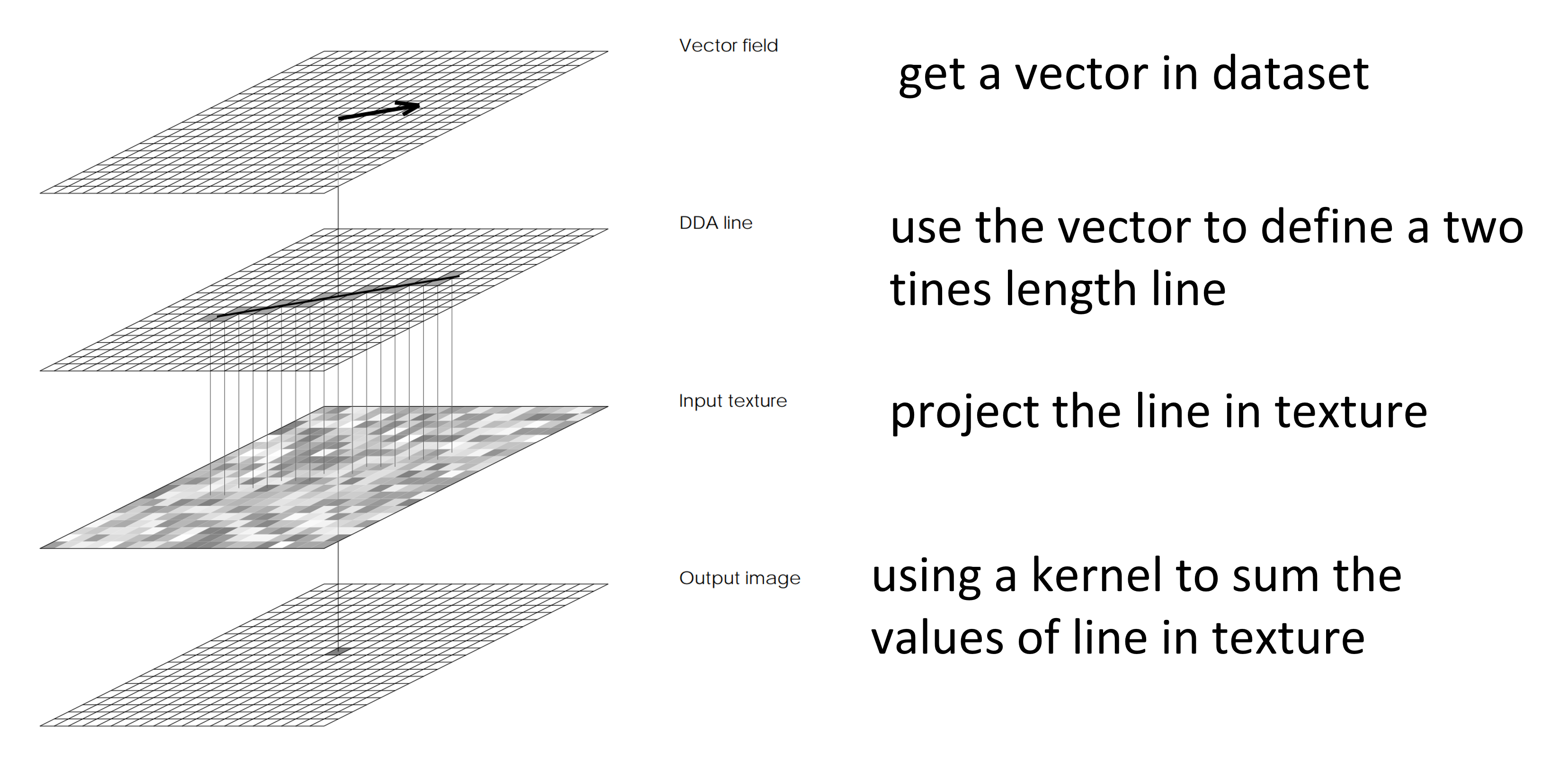
在介绍 LIC 之前，我们先介绍基于栅格化直线和背景纹理之间的卷积融合的方法。在§4.1 和 §6.4 中我们介绍过如何将数学上的连续直线和曲线绘制到像素网格上，这是通过数字微分法（Digital Differential Analyzer, DDA）实现的。在此基础上，如图 25.13 所示，人们提出了数字微分卷积法（DDA-Convolution，DDAC）：（1）对矢量场中的任一点处的矢量，（2）从该点处沿矢量方向，按设定步长 \(L\) 向前后各走一步，得到对应的一条直线段，（3）将这条线段投影到背景纹理图（如：随机生成的噪声背景图）中，（4）在这条线段上对背景纹理进行求卷积，得到该点最终的像素值。

../../_images/visualization-scientific-ddac.png

图 25.13 数字微分卷积法的操作流程。[CL93]#

DDAC 算法对于局部近似成直线的矢量场（如：平流的流场）的效果较好，但是对于尺寸小于 \(2L\) 的复杂结构，或者说曲率较大的点（如：急转弯的流场），这种方法并不准确。而且，简单地应用卷积会自带一个去噪平均化的效果。因此，DDAC 算法难以体现矢量场中的高频的变化，造成细微结构的丢失和信息频率的缺失和不平衡。因此，人们后续提出了 LIC 算法来修缮上述问题。

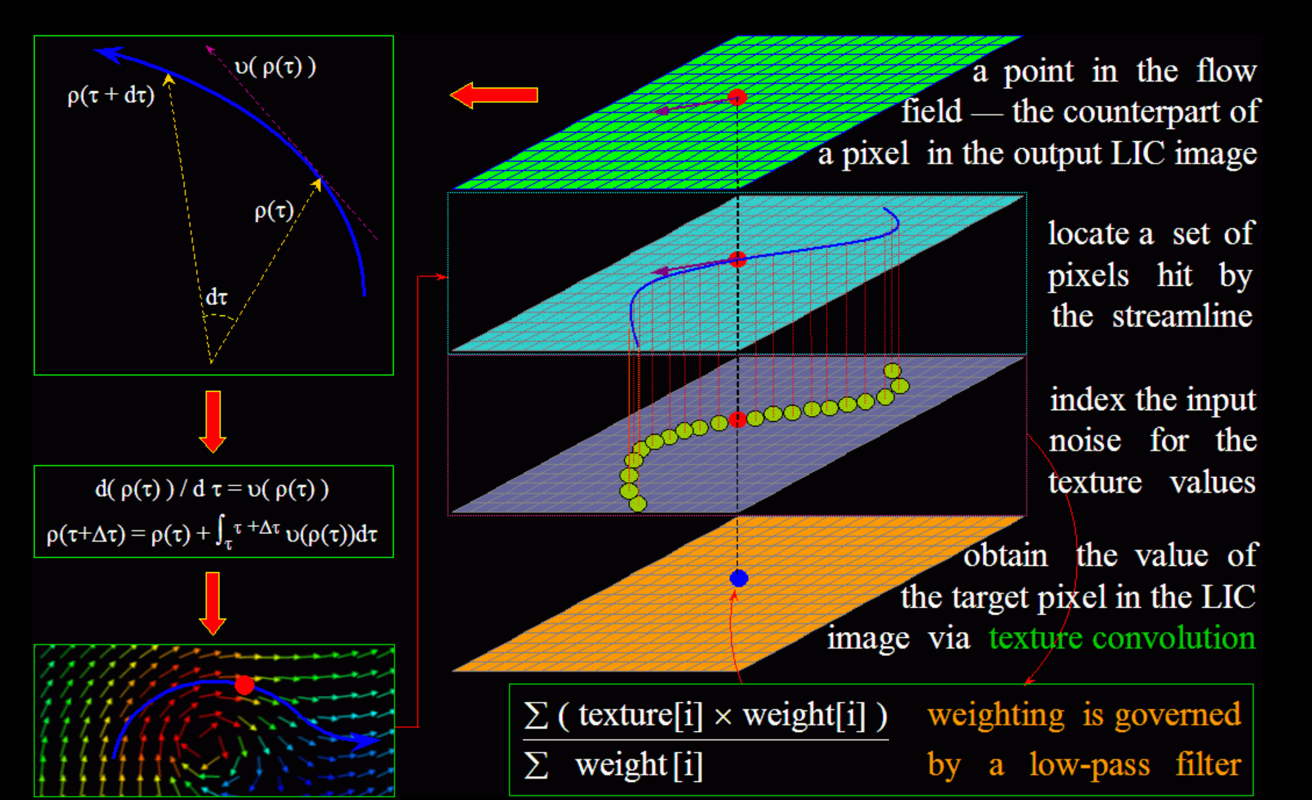
LIC 算法 [CL93] 最初被发表在 1993 年的 SIGGRAPH 上，是在 DDAC 算法的基础上做出的主要改进是：卷积不再沿着切线直线方向，而是改为沿流线进行曲线段上的卷积，以此来解决大曲率处直线近似的精度不够的问题。 在 LIC 算法中，像素点 \({x,y}\) 处的值，同样是沿前向和后向分别沿流线走动一段曲线轨迹得到的，这种双向行走有助于保持单元格对称性。从

\[\begin{split} P_{0} &= (x+0.5, y+0.5)， \\ P_{0}' &= P_{0}， \end{split}\]
出发，前向和后向的步进被表示为：

(25.9)#\[\begin{split} P_{i} &= P_{i-1} + \frac{\boldsymbol{v}(\lfloor P_{i-1} \rfloor)}{|\boldsymbol{v}(\lfloor P_{i-1} \rfloor)|} \Delta s_{i-1}， \\ P_{i}' &= P_{i-1}' - \frac{\boldsymbol{v}(\lfloor P_{i-1}' \rfloor)}{|\boldsymbol{v}(\lfloor P_{i-1}' \rfloor)|} \Delta s'_{i-1} ， \end{split}\]

其中，我们用上标一撇表示后向轨迹，用坐标加 0.5 后向下取整符号来获得距离目标点最近的格点并获取格点上的矢量场采样值 \(\boldsymbol{v}(\lfloor P \rfloor)\)，\(\Delta s\) 与 \(\Delta s'\) 表示步进长度，是沿着平行于矢量场的方向从 \(P_i\) 或 \(P'_i\) 到最近单元格边缘的正负参数距离，需要根据矢量场的网格精度来进行调整。

对于第 \(i\) 段轨迹，我们可以计算出这段轨迹上卷积核函数 \(k(w)\) 的准确积分：

(25.10)#\[ h_{i} = \int_{s_i}^{s_i + \Delta s_i} k(w) dw \]

这个结果将被用作步骤（4）离散卷积中对应像素处背景纹理的权重， 最终图像上应该呈现的结果由 \(F'(x, y)\) 给出：

(25.11)#\[ F'(x, y) = \frac{\sum_{i=0}^l F(\lfloor P_i \rfloor) h_i + \sum_{i=0}^{l'} F(\lfloor P_i' \rfloor) h_i'}{\sum_{i=0}^l h_i + \sum_{i=0}^{l'} h_i'}， \]

其中 \(F(\lfloor P \rfloor)\) 是 \(\lfloor P \rfloor\) 位置处的初始背景像素值。

思考

在式 (25.9) 中，我们只使用了矢量的方向而没有使用大小，大小可以通过颜色映射方法反应到图像中，如图 25.12 右所示。能否将矢量大小也反映在卷积中（如图 25.12 左所示）？

../../_images/visualization-scientific-lic_wind.png

图 25.14 LIC算法效果类似于一堆细沙被强风吹散。[1] © Zhanping Liu#

../../_images/visualization-scientific-lic_pipeline.png

图 25.15 LIC算法流程。[1] © Zhanping Liu#

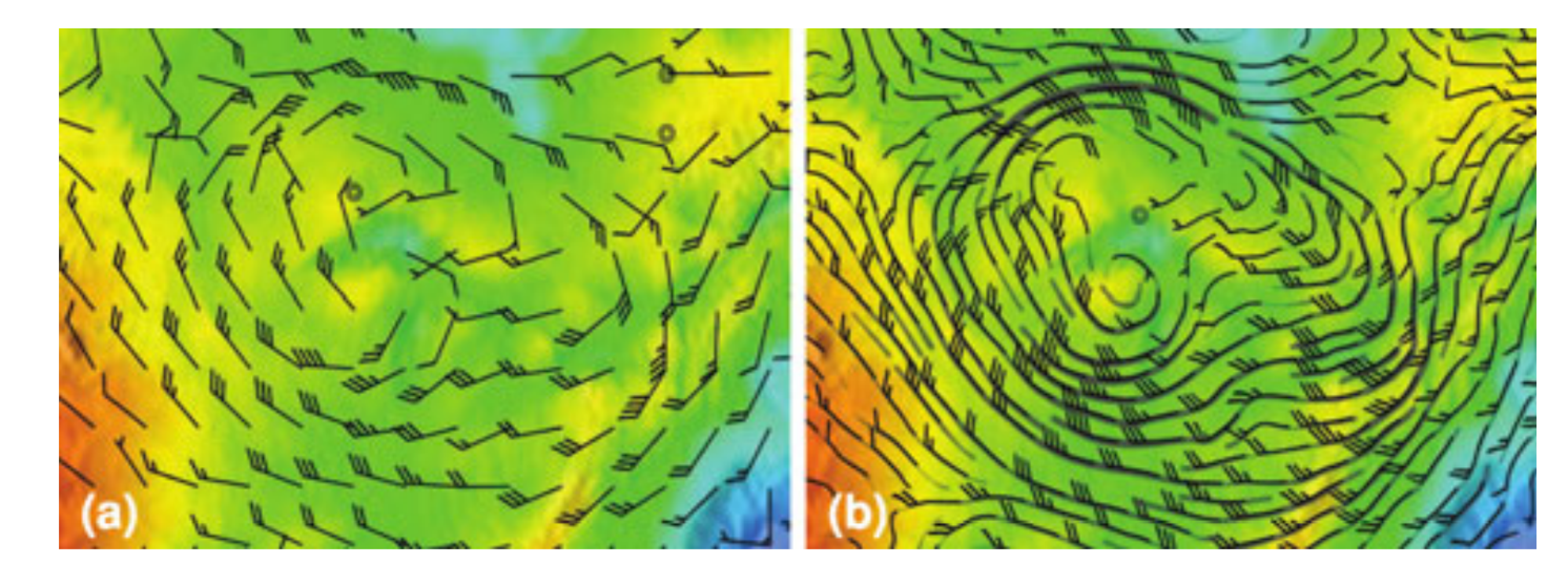
后续人们也提出了若干对 LIC 算法的改进思路。在传统的 LIC 方法中，每个像素点的计算都是独立的，而 TexMap LIC 则通过将 LIC 运算映射到纹理空间中来优化这一过程。 这种方法使得 LIC 能够更好地利用现代图形硬件的能力，尤其是在处理大规模或复杂的矢量场数据时，能够显著提高渲染速度和图像质量。 Volume LIC 是将 LIC 方法扩展到三维空间的一种技术，用于三维矢量场的可视化。它通过在体积数据中沿着矢量流线进行积分卷积，生成能够表现三维流动特性的图像。

25.1.3.5. 其他方法#

其他的矢量场可视化方法还有：流拓扑可视化 (Flow Topology Visualization)，粒子系统 (Particle-based Methods)等，如图 25.16 所示。 矢量场可视化的前沿领域还在探索关于不稳定流（Unsteady Flow）的可视化、可视化算法的加速、结合神经网络表达的可视化方法等等，这里不再展开描述。

../../_images/visualization-scientific-flow_vis.png

图 25.16 多种多样的流场可视化方法。[vW02]#

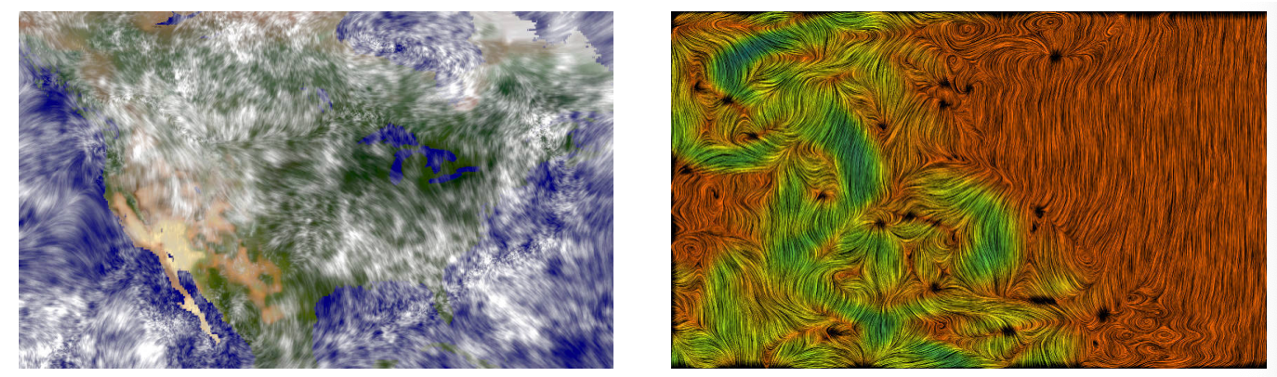
在实际应用中，标量场也常与矢量场一起，被用来表述具有多类型数据的空间信息。 一个常见的组合是天气预报时的温度场和风场，如图 25.17。

../../_images/visualization-scientific-scalar_and_vector.png

图 25.17 由（a）传统风旗和（b）流线与风旗组合描绘的风场和温度场 [PW13]。#

25.1.4. 张量场可视化#

张量场可视化是一种将复杂的多维数据转换成直观图形的技术，广泛应用于材料科学、医学成像、地球物理学等领域。 张量本身并不直观， 为了有效传达其结构和特征，人们发展出了多种可视化手段，与矢量场可视化的思路类似，主要包括基于图元、纹理和几何结构的方法。这些方法从不同角度捕捉张量场的空间分布、方向性和局部变化特征，各具优势与适用场景。

25.1.4.1. 基于图元的可视化#

第一类方法是基于图元（glyph）的可视化。这类方法的核心思想是使用简单的二维或三维几何图形，如箭头、椭球、圆柱或长方体等，将张量的主要信息编码到图形的方向、大小和形状之中。

例如，在一个三维二阶对称张量场中，通过对张量进行特征值分解，可以获得三个正交主方向以及对应的特征值。将这些方向作为几何体的主轴，将特征值映射为主轴的长度，就能构造出反映张量各向异性的椭球图元。

在应力分析、材料科学以及医学图像处理等领域中，图元法被广泛应用。它在医学成像中的一个典型应用是扩散张量成像（Diffusion Tensor Imaging，DTI），每个体素内的张量常被表示为一个椭球体，其中主轴方向对应水分子的主扩散方向，轴长则反映扩散强度。 图 25.18 展示了使用不同类型图元的张量场可视化效果。

../../_images/visualization-scientific-hyperglyph.png

图 25.18 基于图元的张量可视化，第一行采用椭球体（ellipsoids）图元，第二行采用超二次曲面（superquadrics）图元。左：不同张量取值的图元形状；中：脑 DT-MRI 数据集的二维切片的可视化；右：3D 脑 DT-MRI 数据集可视化。。[Kin04]#

这种方法的优点在于直观、可解释，能够清晰地传达局部的张量特性。但当张量场密度较高时，图元可能会发生严重遮挡和重叠，从而降低整体可读性。

25.1.4.2. 基于纹理的可视化#

基于纹理的可视化方法通过将张量信息映射到空间中的连续纹理图案来传达其分布特征。纹理可以是规则的线条、条带，也可以是随机噪声图案。可视化过程中，张量场首先被简化为一组主要方向信息，再控制纹理图案的走向、密度和颜色，以反映张量的主方向、各向异性程度和其他不变量特征。

这种方法具有显著的全局连续性优势，能够在整个可视区域内统一展现张量变化趋势，避免了图元方法在稠密场中的离散感。 非常适合用于流体力学、弹性力学等需要展示连续张量分布的场景，但其计算和渲染成本较高，且细节控制上不如图元法灵活。

这类方法的很多研究是基于纹理的矢量场可视化的拓展，如：LIC 的变体 HyperLIC [ZP03]；结合三维噪声场、并使用体渲染方法（我们将在下一小节介绍体渲染）渲染张量图元的可视化方法 [SEHWigstrom02]。这里不再详述。

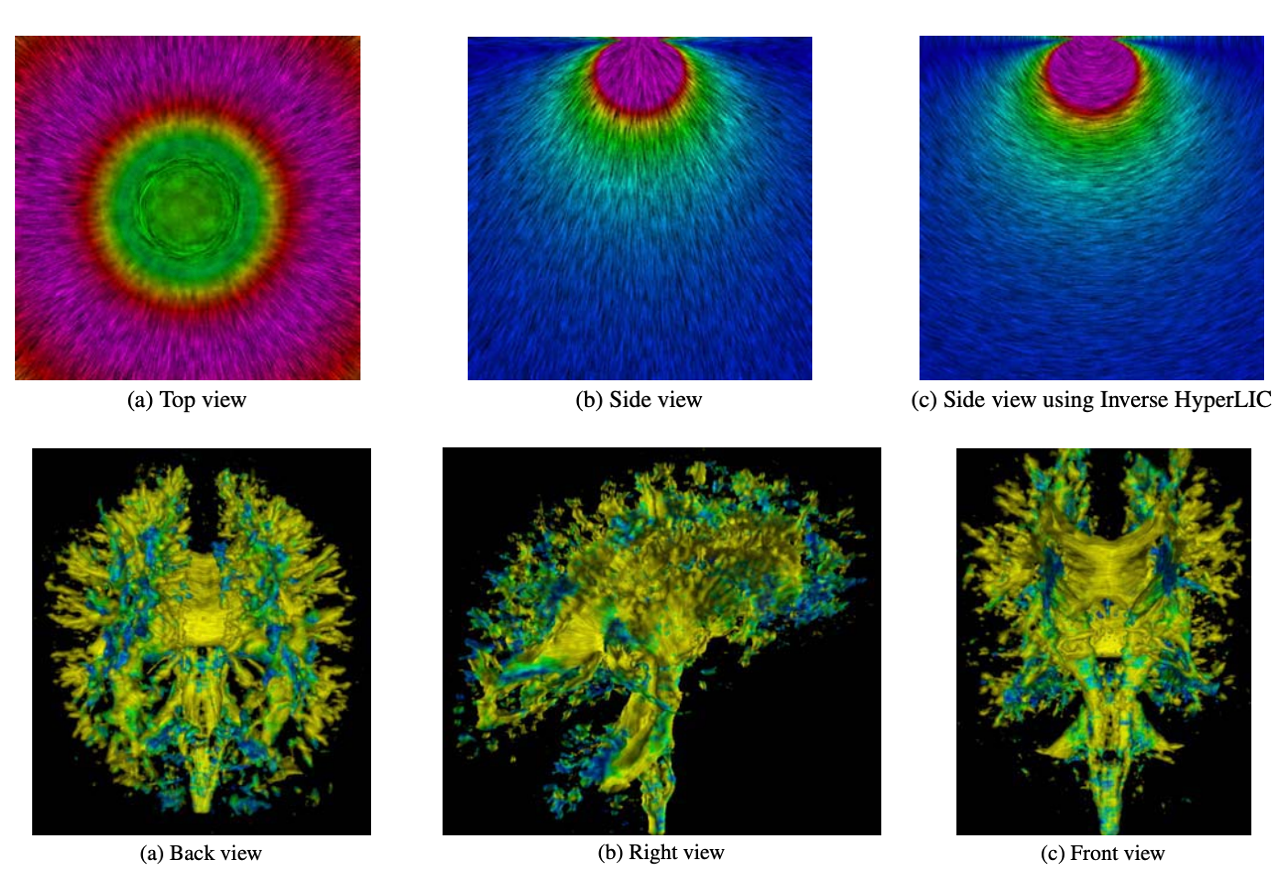
../../_images/visualization-scientific-hyperLIC.png

图 25.19 基于 HyperLIC 的张量可视化。第一行：二维 HyperLIC，不同视角下，单点载荷下的应力张量可视化；第二行：三维 HyperLIC，不同视角下，MRI 脑弥散张量（diffusion tensor）数据的可视化。[ZP03]#

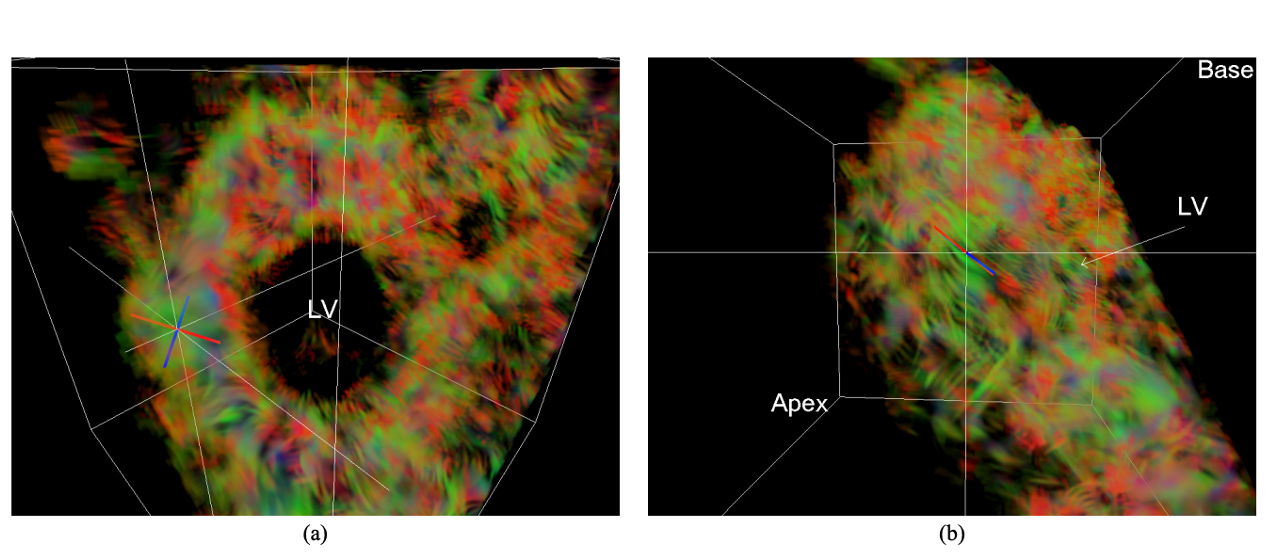
../../_images/visualization-scientific-3DNoiseField.png

图 25.20 基于三维噪声场的张量可视化：不同视角下，心肌应变率（strain rate）数据的张量可视化，该数据是二维张量，用于刻画张量的平面图元被置于左心壁。[SEHWigstrom02]#

25.1.4.3. 超流线#

基于几何结构的可视化方法的代表性技术是超流线（hyperstreamlines）。在矢量场中，流线体现局部向量方向。而在张量场中，如果我们将张量的主方向之一当作“流动方向”，沿该方向跟踪曲线，并在垂直截面平面内用椭圆或其他形变展现张量在该点的其他主值和主方向，就得到超流线，如。

超流线同时保留空间走向（第一主方向）与局部张量形态（其他特征方向），在一条曲线上把张量随空间变化的特征“画出来”，同时展示张量的主导流动趋势和局部各向异性形态，因此在材料科学和生物组织建模中尤其重要。例如，在DTI中，神经纤维束的走向可通过对主扩散方向进行超流线跟踪而还原，并通过截面上的椭圆形状直观反映各向异性扩散程度。该方法具有很高的表达能力和三维结构感，但也面临遮挡、过度密集等可视化挑战。

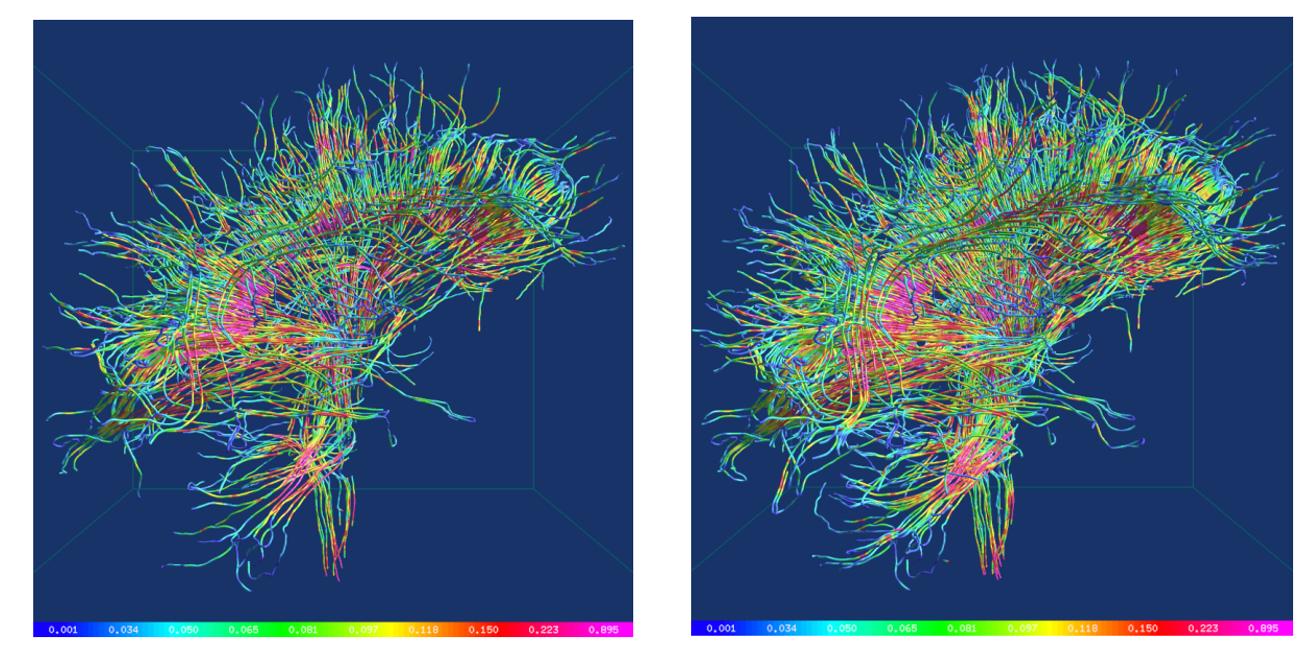
../../_images/visualization-scientific-hyperStreamline.png

图 25.21 基于超流线的张量可视化：脑扩散张量数据的可视化。利用各向异性播种策略和主特征向量方向生成超流线。左：500 条；右：1200条。[SP04]#

每种类型的张量场可视化方法都有其特定的应用场景和优势，选择哪一种取决于要可视化的数据类型和需要强调的数据特征。例如，图元适合强调数据点的局部特征，而纹理和超流线则更适合展示数据的整体流动和结构。图 25.22 给出相应的张量可视化效果。

../../_images/visualization-scientific-tensor_types.png

图 25.22 三种张量可视化的例子图。#