铰链刚体

22.3. 铰链刚体#

在一些特殊的场景中，还会出现一些铰链刚体（articulated rigid body），即通过一些关节（joint）连接成一体的多个刚体。常见的铰链刚体包括人体骨骼、机械臂、门窗、车辆等，在机器人学、人体动画、具身控制等应用场景中出现频率尤其多。在铰链刚体仿真中，我们需要额外处理由关节带来的约束力，这个约束力不像碰撞处理那样容易给出显式的形式，往往需要借助其他的形式隐式地引入到系统中。

在本节，我们会介绍两种处理铰链刚体的方法——约束法和广义坐标法。这两种方法的本质不同在于描述关节的方式，前者是使用关于速度的约束来描述关节，后者使用关节的自由度来描述。

22.3.1. 约束法#

图 22.8 中包含了常见的四种关节，球关节（ball joint）允许两个刚体围绕着一个公共点做自由旋转，但不允许该点的相对位移；万向节（universal joint）包含两个旋转轴，允许刚体之间做两个自由度的旋转；合页（hinge joint）允许两个刚体围绕同一个轴转动；滑动关节（slider joint）允许两个刚体之间产生单个方向的相对滑动，不允许刚体之间的相对转动。

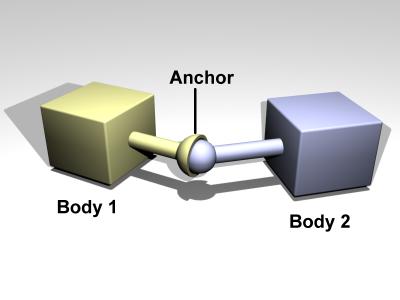球关节 球关节
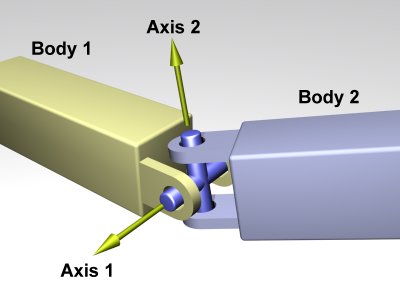万向节 万向节
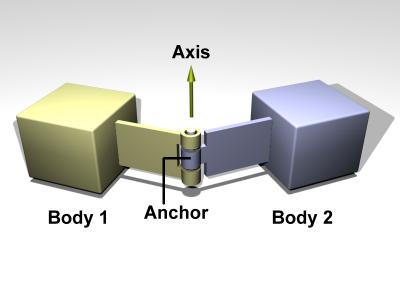合页 合页
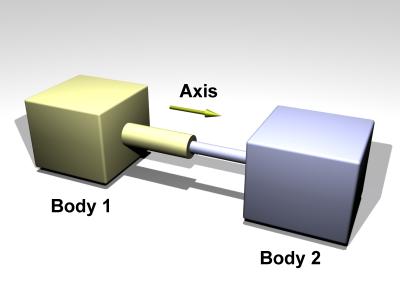滑动关节 滑动关节

图 22.8 一些常见的关节[1]#

现在我们假设场景中只有一个由单个关节连接两个刚体的铰链刚体。设关节的位置在两个刚体的标准构型下坐标分别为 \(\boldsymbol X_1\) 和 \(\boldsymbol X_2\)（对于滑动关节这个定义并不重要），当前两个刚体的旋转矩阵分别为 \(\boldsymbol R_1\) 和 \(\boldsymbol R_2\)，质心位置分别为 \(\boldsymbol c_1\) 和 \(\boldsymbol c_2\)。接下来我们分步推导这个系统要如何模拟。

22.3.1.1. 用约束描述关节#

球关节对两个刚体运动的限制即为 \(\boldsymbol X_1\) 和 \(\boldsymbol X_2\) 在刚性变换后的位置相同，即

(22.10)#\[ \boldsymbol R_1\boldsymbol X_1+\boldsymbol c_1=\boldsymbol R_2\boldsymbol X_2+\boldsymbol c_2。 \]

在约束法中，我们需要将关节带来的限制表示成关于速度和角速度的约束，这个约束可以由式 (22.10) 两端关于时间求导得到：

(22.11)#\[ \boldsymbol\omega_1\times\boldsymbol R_1\boldsymbol X_1+\boldsymbol v_1-\boldsymbol\omega_2\times\boldsymbol R_2\boldsymbol X_2-\boldsymbol v_2=\mathbf 0。 \]

若将 \(\boldsymbol R_1\) 和 \(\boldsymbol R_2\) 视为常量，我们可以将式 (22.11) 中的约束写成矩阵的形式：

(22.12)#\[\begin{split} \boldsymbol J_\mathrm{ball}\boldsymbol u\mathrel{\mathop:}=\begin{pmatrix}\mathbf I&-[\boldsymbol R_1\boldsymbol X_1]&-\mathbf I&[\boldsymbol R_2\boldsymbol X_2]\end{pmatrix}\begin{pmatrix}\boldsymbol v_1\\\boldsymbol\omega_1\\\boldsymbol v_2\\\boldsymbol\omega_2\end{pmatrix}=\mathbf 0， \end{split}\]

其中 \(\boldsymbol J_\mathrm{ball}\) 是速度约束关于两个刚体的速度与角速度的雅可比矩阵；并且为了方便推导，我们将所有刚体的速度与角速度堆叠成向量 \(\boldsymbol u\)。

万向节对两个刚体运动的限制在球关节的基础上增加了一条：两刚体之间不能沿一个特定轴 \(\boldsymbol a\)（即与图 22.8 中万向节两个轴垂直的向量，这是一个随时间变化的量）发生相对旋转，即

(22.13)#\[ (\boldsymbol\omega_1-\boldsymbol\omega_2)\cdot\boldsymbol a=0。 \]

提示

读者不妨想一想：为何相对角速度等于 \(\boldsymbol\omega_1-\boldsymbol\omega_2\)？

因此万向节约束的雅可比矩阵可以表示成

(22.14)#\[\begin{split} \boldsymbol J_\mathrm{universal}=\begin{pmatrix}\mathbf I&-[\boldsymbol R_1\boldsymbol X_1]&-\mathbf I&[\boldsymbol R_2\boldsymbol X_2]\\\mathbf 0&\boldsymbol a^\top&\mathbf 0&-\boldsymbol a^\top\end{pmatrix}。 \end{split}\]

合页与万向节很相似，在球关节约束的基础上增加两个轴 \(\boldsymbol a_1\) 和 \(\boldsymbol a_2\) 上不能产生相对旋转即可，因此我们可以直接写出合页约束的雅可比矩阵：

(22.15)#\[\begin{split} \boldsymbol J_\mathrm{hinge}=\begin{pmatrix}\mathbf I&-[\boldsymbol R_1\boldsymbol X_1]&-\mathbf I&[\boldsymbol R_2\boldsymbol X_2]\\\mathbf 0&\boldsymbol a_1^\top&\mathbf 0&-\boldsymbol a_1^\top\\\mathbf 0&\boldsymbol a_2^\top&\mathbf 0&-\boldsymbol a_2^\top\end{pmatrix}。 \end{split}\]

滑动关节要求两个刚体的旋转完全同步，并且只能在一个轴的方向上产生相对位移。前者可以表示成 \(\boldsymbol\omega_1-\boldsymbol\omega_2=\mathbf 0\)，后者可以在垂直于该轴的平面上取两个互相垂直的向量 \(\boldsymbol a_1\) 和 \(\boldsymbol a_2\)，则相对速度在这两个向量上的投影均为 \(0\)。由此可得滑动关节约束的雅可比矩阵为：

(22.16)#\[\begin{split} \boldsymbol J_\mathrm{slider}=\begin{pmatrix}\mathbf 0&\mathbf I&0&-\mathbf I\\\boldsymbol a_1^\top&\mathbf 0&-\boldsymbol a_1^\top&\mathbf 0\\\boldsymbol a_2^\top&\mathbf 0&-\boldsymbol a_2^\top&\mathbf 0\end{pmatrix}。 \end{split}\]

22.3.1.2. 重新表达刚体时间积分#

在 §22.1.3 的步骤中，对速度和角速度的时间积分可表示成如下等式：

\[\begin{split} &\boldsymbol v_i^\mathrm{new}=\boldsymbol v_i+hm_i^{-1}\boldsymbol F_i，\\ &\boldsymbol\omega_i^\mathrm{new}=\boldsymbol\omega_i+h\boldsymbol I_i^{-1}(\boldsymbol\tau_i-\boldsymbol\omega_i\times\boldsymbol I_i\boldsymbol\omega_i)， \end{split}\]

其中下标 \(i\in\{1,2\}\) 表明该物理量属于哪个刚体，这里我们用上标 \(\mathrm{new}\) 表示下一个时间步的量，无上标表示当前时刻的量；这两个式子还可以统一写成如下的矩阵形式：

\[\begin{split} \begin{pmatrix}\boldsymbol v_i^\mathrm{new}\\\boldsymbol\omega_i^\mathrm{new}\end{pmatrix}=\begin{pmatrix}\boldsymbol v_i\\\boldsymbol\omega_i\end{pmatrix}+h\begin{pmatrix}m_i\mathbf I&\mathbf 0\\\mathbf 0&\boldsymbol I_i\end{pmatrix}^{-1}\begin{pmatrix}\boldsymbol F_i\\\boldsymbol\tau_i-\boldsymbol\omega_i\times\boldsymbol I_i\boldsymbol\omega_i\end{pmatrix}。 \end{split}\]

我们记 \(\boldsymbol M_i=\begin{pmatrix}m_i\mathbf I&\mathbf 0\\\mathbf 0&\boldsymbol I_i\end{pmatrix}\)，\(\boldsymbol\xi_i=\begin{pmatrix}\boldsymbol F_i\\\boldsymbol\tau_i-\boldsymbol\omega_i\times\boldsymbol I_i\boldsymbol\omega_i\end{pmatrix}\)，则上式可继续简化为

\[ \boldsymbol u_i^\mathrm{new}=\boldsymbol u_i+h\boldsymbol M_i^{-1}\boldsymbol\xi_i。 \]

我们还可以将 \(i=1\) 和 \(i=2\) 的情形合并到一起，记 \(\boldsymbol M=\begin{pmatrix}\boldsymbol M_1&\mathbf 0\\\mathbf 0&\boldsymbol M_2\end{pmatrix}\)，\(\boldsymbol\xi=\begin{pmatrix}\boldsymbol\xi_1\\\boldsymbol\xi_2\end{pmatrix}\)，即可得到重新表达成矩阵形式的刚体时间积分步骤：

(22.17)#\[ \boldsymbol u^\mathrm{new}=\boldsymbol u+h\boldsymbol M^{-1}\boldsymbol\xi。 \]

22.3.1.3. 带约束的时间积分#

现在我们要为式 (22.17) 的时间积分加上由关节带来的速度约束，即 \(\boldsymbol J\boldsymbol u^\mathrm{new}=\mathbf 0\)，其中 \(\boldsymbol J\) 根据关节的种类取 \(\boldsymbol J_\mathrm{ball}\)、\(\boldsymbol J_\mathrm{universal}\)、\(\boldsymbol J_\mathrm{hinge}\) 或 \(\boldsymbol J_\mathrm{slider}\) 中的一种。关节之所以能让速度满足这样的约束，是因为提供了一个额外的约束力，也即在考虑到关节的作用时，式 (22.17) 等号右边要再加一项。现在我们假设关节是光滑的（不会导致能量的损耗），则它的约束就是理想约束；根据理论力学中的定义，约束力的虚功为 \(0\)，也即约束力方向应与任意满足 \(\boldsymbol{Jw}=\mathbf 0\) 的速度 \(\boldsymbol w\) 正交，也就是与 \(\ker\boldsymbol J\) 正交，这说明约束力属于 \(\boldsymbol J\) 的行空间，我们用 \(\boldsymbol J^\top\boldsymbol\lambda\) 表示约束力。

至此，我们的时间积分从式 (22.17) 变成了如下关于 \(\boldsymbol\xi\) 和 \(\boldsymbol u^\mathrm{new}\) 的线性方程组：

\[\begin{split} \begin{cases} \boldsymbol u^\mathrm{new}=\boldsymbol u+h\boldsymbol M^{-1}(\boldsymbol\xi+\boldsymbol J^\top\boldsymbol\lambda)\\ \boldsymbol J\boldsymbol u^\mathrm{new}=\mathbf 0 \end{cases}。 \end{split}\]

将 \(\boldsymbol u^\mathrm{new}\) 代入 \(\boldsymbol J\boldsymbol u^\mathrm{new}=\mathbf 0\) 可得到关于 \(\boldsymbol\lambda\) 的线性系统：

(22.18)#\[ \boldsymbol J\boldsymbol M^{-1}\boldsymbol J^\top\boldsymbol\lambda=-\frac 1h\boldsymbol{Ju}-\boldsymbol J\boldsymbol M^{-1}\boldsymbol\xi。 \]

不难看出 \(\boldsymbol J\boldsymbol M^{-1}\boldsymbol J^\top\) 是正定的，因此有很多高效的求解算法；在求得 \(\boldsymbol\lambda\) 之后代入第一个方程即可得到下个时间步的速度与角速度。

至此我们已经完全可以模拟带有一个关节、两个刚体的场景了，对于多个关节、多个刚体的场景只需要我们关节连接的拓扑结构构造好 \(\boldsymbol J\) 和 \(\boldsymbol M\) 的形式，也能用同样的方法求出 \(\boldsymbol u^\mathrm{new}\)，具体的实现方法交给读者思考。

22.3.2. 广义坐标法#

在约束法中我们使用了刚体的所有自由度来表示运动，若场景中有 \(N\) 个刚体，则表示速度的向量 \(\boldsymbol u\) 就有 \(6N\) 维，并在此基础上通过一系列关于 \(\boldsymbol u\) 的约束方程来减少整个系统的自由度。因此在场景中的关节数量较多时，约束法的计算量就会较大，这从式 (22.18) 中线性系统的维数（等于减少的自由度数量）就可以看出来。

广义坐标法则追求使用最少的自由度表示系统中的刚体，因此用于表示系统状态的坐标维数恰好等于铰链刚体剩余的自由度数量，并且这些坐标必须能够表达出全部刚体的旋转矩阵以及质心位置，这套坐标就称为广义坐标。广义坐标的选取有多种，对于图 22.8 中的关节，我们提供一种最简便的方式。我们仍然假定系统中只有两个由关节连接的刚体，编号为 \(1\) 和 \(2\)，选取广义坐标的前 \(6\) 维分别是刚体 \(1\) 的质心位置以及用欧拉角表示的旋转，再根据关节的种类选取广义坐标剩下的维度：

  1. 球坐标：广义坐标的后 \(3\) 维选成刚体 \(2\) 相对刚体 \(1\) 旋转的欧拉角。

  2. 万向节：广义坐标的后 \(2\) 维选成万向节两个轴方向的旋转角度。

  3. 合页：广义坐标的最后一维选成两刚体共轴方向的旋转角度。

  4. 滑动关节：广义坐标的最后一维选成两刚体沿轴方向的相对滑动距离。

如何利用这些广义坐标还原出两个刚体的质心位置 \(\boldsymbol c_1\)、\(\boldsymbol c_2\) 以及旋转矩阵 \(\boldsymbol R_1\)、\(\boldsymbol R_2\) 留给读者练习。记自由度数量为 \(n\)，广义坐标为 \(\boldsymbol q=\begin{pmatrix}q_1&\cdots&q_n\end{pmatrix}^\top\)，我们知道两个刚体的质心位置可以表示成广义坐标的函数 \(\boldsymbol c_i(q_1,\cdots,q_n)\)，旋转矩阵也同理 \(\boldsymbol R_i(q_1,\cdots,q_n)\)（\(i\in\{1,2\}\)，下同），对质心位置求导可以得到

(22.19)#\[ \boldsymbol v_i=\frac{\partial\boldsymbol c_i}{\partial\boldsymbol q}\frac{\mathrm d\boldsymbol q}{\mathrm dt}=\mathrel{\mathop:}\boldsymbol{T^v}_i\dot{\boldsymbol q}， \]

这里的 \(\boldsymbol{T^v}_i\) 是质心位置关于广义坐标的雅可比矩阵，为了防止与约束法中的记号冲突，我们使用 \(\boldsymbol T\) 表示。事实上，角速度也可以表示成类似的形式

(22.20)#\[ \boldsymbol\omega=\boldsymbol{T^\omega}_i\dot{\boldsymbol q}， \]

但这里的 \(\boldsymbol{T^\omega}_i\) 不再是雅可比矩阵，通过下面的证明过程可以看出其构造方式。

Proof. 我们已经知道 \(\dot{\boldsymbol R}_i=[\boldsymbol\omega_i]\boldsymbol R_i\)，因此

\[ [\boldsymbol\omega_i]=\dot{\boldsymbol R}_i\boldsymbol R_i^\top=\sum_{j=1}^n\frac{\partial\boldsymbol R_i}{\partial q_j}\dot q_j\boldsymbol R_i^\top。 \]

由正交矩阵的性质我们有 \(\boldsymbol R_i\boldsymbol R_i^\top=\mathbf I\)，常量的偏导数为 \(0\)，因此得到

\[ \frac{\partial(\boldsymbol R_i\boldsymbol R_i^\top)}{\partial q_j}=\frac{\partial\boldsymbol R_i}{\partial q_j}\boldsymbol R_i^\top+\boldsymbol R_i\frac{\partial\boldsymbol R_i^\top}{\partial q_j}=\mathbf 0， \]

即 \(\frac{\partial\boldsymbol R_i}{\partial q_j}\boldsymbol R_i^\top\) 是一个三阶反对称矩阵。于是存在向量 \(\boldsymbol t_{ij}\) 满足 \([\boldsymbol t_{ij}]=\frac{\partial\boldsymbol R_i}{\partial q_j}\boldsymbol R_i^\top\)，因此 \([\boldsymbol\omega_i]=\sum_{j=1}^n\dot q_j[\boldsymbol t_{ij}]\)，也即 \(\boldsymbol\omega_i=\sum_{j=1}^n\dot q_j\boldsymbol t_{ij}\)。因此我们有

\[ \boldsymbol\omega_i=\begin{pmatrix}\boldsymbol t_{i1}&\cdots&\boldsymbol t_{in}\end{pmatrix}\dot{\boldsymbol q}。 \]

在没有关节时，刚体的运动方程可以表示为

\[\begin{split} \boldsymbol M_i\dot{\boldsymbol u}_i+\begin{pmatrix}\mathbf 0\\\boldsymbol\omega_i\times\boldsymbol I_i\boldsymbol\omega_i\end{pmatrix}=\begin{pmatrix}\boldsymbol F_i\\\boldsymbol\tau_i\end{pmatrix}。 \end{split}\]

将式 (22.19) 和 (22.20) 代入上式可得

\[\begin{split} \boldsymbol M_i\dot{\boldsymbol T}_i\dot{\boldsymbol q}+\boldsymbol M_i\boldsymbol T_i\ddot{\boldsymbol q}+\begin{pmatrix}\mathbf 0\\\boldsymbol{T^\omega}_i\dot{\boldsymbol q}\times\boldsymbol I_i\boldsymbol{T^\omega}_i\dot{\boldsymbol q}\end{pmatrix}=\begin{pmatrix}\boldsymbol F_i\\\boldsymbol\tau_i\end{pmatrix}， \end{split}\]

其中 \(\boldsymbol T_i=\begin{pmatrix}\boldsymbol{T^v}_i\\\boldsymbol{T^\omega}_i\end{pmatrix}\)。在模拟过程中，我们会维护广义坐标 \(\boldsymbol q\) 以及广义速度 \(\dot{\boldsymbol q}\)，在每个时间步需要求 \(\ddot{\boldsymbol q}\)。但上式的方程是超定的（方程个数为 \(6N\)，大于自由度数量 \(n\)），因为这个方程是我们借助 \(\boldsymbol u=\boldsymbol T\dot{\boldsymbol q}\) 将广义速度转化到了全自由度空间下的运动方程，这里 \(\boldsymbol T=\begin{pmatrix}\boldsymbol T_1\\T_2\end{pmatrix}\)，我们还要在等式两边左乘 \(\boldsymbol T^\top\) 投影回广义坐标的空间：

(22.21)#\[ \sum_{i=1}^2[\boldsymbol T_i^\top\boldsymbol M_i\dot{\boldsymbol T}_i\dot{\boldsymbol q}+\boldsymbol T_i^\top\boldsymbol M_i\boldsymbol T_i\ddot{\boldsymbol q}+(\boldsymbol{T^\omega}_i)^\top(\boldsymbol{T^\omega}_i\dot{\boldsymbol q}\times\boldsymbol I_i\boldsymbol{T^\omega}_i\dot{\boldsymbol q})]=\sum_{i=1}^2[(\boldsymbol{T^v}_i)^\top\boldsymbol F_i+(\boldsymbol{T^\omega}_i)^\top\boldsymbol\tau_i]。 \]

求解出 \(\ddot{\boldsymbol q}\) 后可以通过时间积分求出下一个时刻的广义速度 \(\dot{\boldsymbol q}\)，再进行时间积分得到下一时刻的广义坐标 \(\boldsymbol q\)。

22.3.3. 两种方法的比较#

约束法实现简单，并且由于存储的状态量就是位置、旋转、速度和角速度本身，它可以很轻松地与其他物理系统耦合。但在关节较多时，约束法要求解一个庞大的线性系统，影响模拟效率；此外，仅仅满足速度约束并不能保证模拟过程中关节的约束能够时刻满足（想一想，为什么），这就导致模拟过程中关节可能出现错位等现象。

广义坐标法在关节较多时能够达到更高的计算效率，因为其线性系统的阶数等于自由度的数量；并且由于模拟过程中的状态量是由广义坐标间接表示出来的，关节的约束必然能够满足。但是这个方法的普适性不高，在关节连接情况复杂时（如形成一个环）往往不好选择广义坐标；且由于状态量需要间接计算，它也难以与其他物理系统耦合。