7.1. 图像滤波#

图像滤波（image filtering） 是一种图像处理技术，用于改善图像质量、去除噪声和突出图像中的特定特征。它的核心是卷积（convolution），不同的卷积核就对应着不同的功能。我们下面先介绍卷积的数学原理，再介绍几种常用的滤波器。

7.1.1. 卷积#

在一维情况下，两个连续函数 \(f(t)\) 和 \(g(t)\) 的卷积 \(h(t)\) 定义为：

(7.1)#\[ h(t) = f * g = \int_{-\infty}^{\infty} f(\tau) g(t-\tau) d\tau \]

在离散情况下我们可以给出对应的形式：

(7.2)#\[ h(t) = \sum_{\tau=-\infty}^{+\infty}f[\tau]g[t-\tau] \]

对于滤波而言，我们可以认为公式 (7.2) 中的 \(f\) 是我们的输入信号，\(g\) 称为卷积核（kernel），或者滤波器（filter），\(h\) 是最终输出的信号。尽管公式 (7.2) 中的求和上下限是无穷，我们可以暂时假定 \(f\) 和 \(g\) 都是有限的数组，在范围外都取 0。注意到 \(g[t-\tau]\) 可以看成是先将 \(g[\tau]\) 镜像然后再向右平移 \(t\) 位：\(g[0]\) 被移到了 \(g[t]\)，\(g[1]\) 被移到了 \(g[t-1]\)，以此类推。因此得到 \(h[t]\) 的过程相当于我们将镜像过的 \(g[\tau]\) 在 \(f[\tau]\) 上滑动 \(t\) 位，然后把两个数组对应位置相乘再相加，如图 7.2 所示。

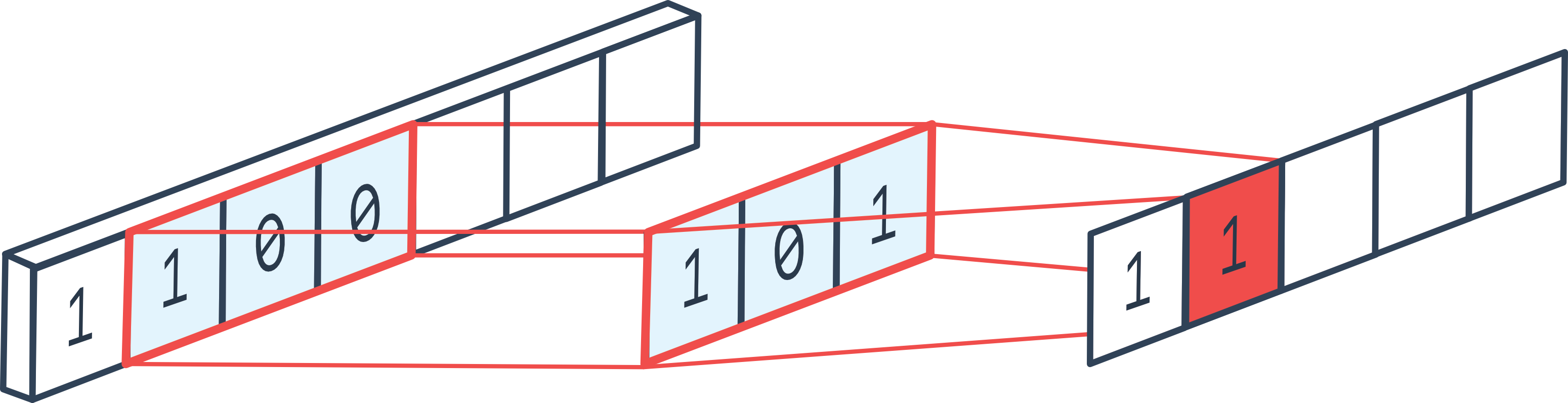
../../_images/conv1d.png — 图 7.2 一维卷积的过程#

一般情况我们会把卷积核取得比较短，比如我们可以取一个全为 \(1/3\) 的长度为 3 的数组，那么卷积的结果 \(h[t]\) 就是把 \(f[t]\) 相邻的三个数相加起来平均，此时卷积就是一个滑动窗口平均的过程。二维的卷积我们可以类似的定义：

(7.3)#\[ h[x,y]=\sum_{u=-\infty}^{+\infty}\sum_{v=-\infty}^{+\infty}f[u,v]g[x-u,y-v] \]

公式 (7.3) 描述的过程如图 7.3 所示。

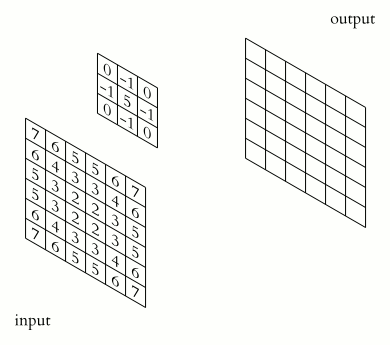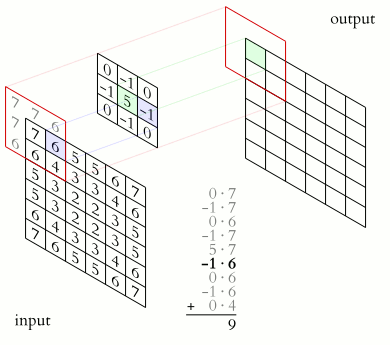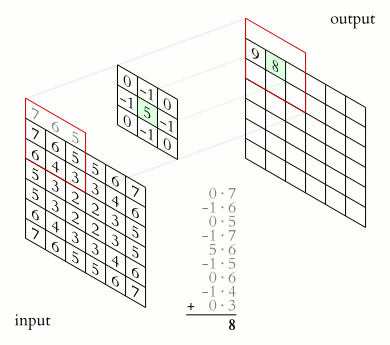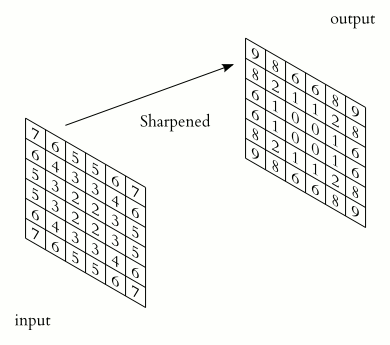
../../_images/conv2d.gif — 图 7.3 二维卷积的过程[1]#

我们在 §5 介绍了傅里叶变换，可以将一个时域的信号 \(f(t)\) 变换到频域 \(F(\omega) = \mathcal{F}(f(t))\)，提供一个新的视角。事实上，卷积与傅里叶变换密切相关，由卷积定理（convolution theorem） 给出：函数卷积的傅里叶变换是函数傅里叶变换的乘积，函数乘积的傅里叶变换是函数傅里叶变换的卷积。对应的数学表述为：

(7.4)#\[\begin{split} \begin{aligned} \mathcal{F}(f*g) &= \mathcal{F}(f(t)) \cdot \mathcal{F}(g(t)) \\ \mathcal{F}(f\cdot g) &= \mathcal{F}(f(t)) * \mathcal{F}(g(t)) \end{aligned} \end{split}\]

这个定理揭示了卷积和乘积在时域和频域中可以相互转换。我们使用卷积进行图片滤波，其实可以看成是对其频域进行乘积变换。我们在图 5.6 中展示了频谱可以直接反映图片的特征，那么针对性设计卷积核就能达到想要的滤波效果。

7.1.2. 图像模糊#

最简单的模糊滤波器是均值滤波器（mean filter），定义为：

(7.5)#\[\begin{split} \begin{bmatrix} h[-k,-k]&\cdots&h[-k,0]&\cdots&h[-k,k]\\ \vdots&\ddots&\vdots&\ddots&\vdots\\ h[0,-k]&\cdots&h[0,0]&\cdots&h[0,k]\\ \vdots&\ddots&\vdots&\ddots&\vdots\\ h[k,-k]&\cdots&h[k,0]&\cdots&h[k,k] \end{bmatrix}=\frac 1{(2k+1)^2} \begin{bmatrix} 1&\cdots&1&\cdots&1\\ \vdots&\ddots&\vdots&\ddots&\vdots\\ 1&\cdots&1&\cdots&1\\ \vdots&\ddots&\vdots&\ddots&\vdots\\ 1&\cdots&1&\cdots&1 \end{bmatrix} \end{split}\]

根据卷积的定义，均值滤波器的作用就是取临近的 \((2k+1) \times (2k+1)\) 个像素求平均，其效果如图 7.4 所示。

../../_images/blur_original.png — 图 7.4 从左到右：原图，使用 \(3\times 3\) 的均值滤波，使用 \(5 \times 5\) 的均值滤波#

../../_images/blur_3x3.png — 图 7.4 从左到右：原图，使用 \(3\times 3\) 的均值滤波，使用 \(5 \times 5\) 的均值滤波#

从频域上我们也能理解均值滤波器为什么能够模糊化。如图 7.5 所示，均值滤波器的傅里叶变换呈现中间值大，边缘值小的趋势，于是当其与图像的频谱相乘时，就保留了中心的低频部分，而去除的高频部分。

../../_images/mean-filter.png — 图 7.5 均值滤波器的傅里叶变换#

然而从图 7.5 中我们也能发现，均值滤波器的频谱并不是严格的只有低频部分，还有十字星形向外放射的部分。这导致图片中的一部分高频信息可能被错误地保留了下来，造成视觉上的走样。如图 7.6 所示，使用均值滤波可能造成细节的错误。

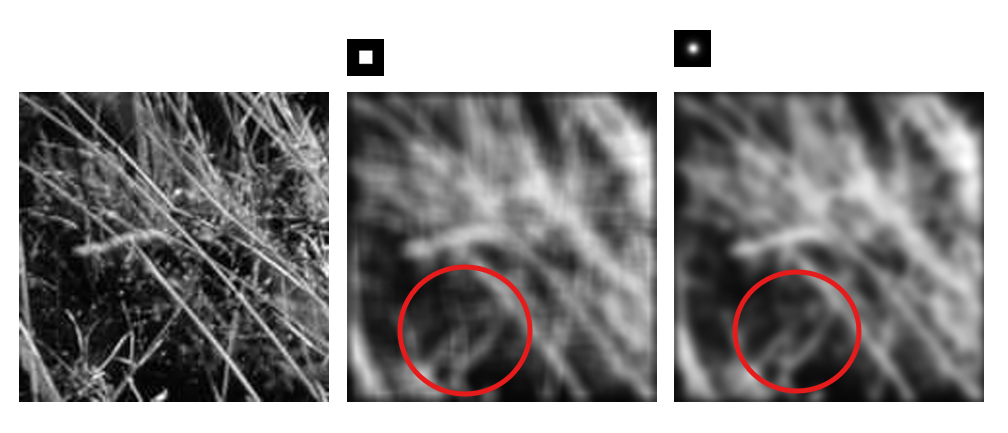
../../_images/ringing.png — 图 7.6 从左到右：原图，使用均值滤波，使用高斯滤波 from Rutgers CS334#

高斯滤波器（Gaussian filter） 是效果更好的模糊滤波器，它的连续形式为：

(7.6)#\[ g(x, y) = \frac{1}{2\pi \sigma^2} \exp(-\frac{x^2+y^2}{2\sigma^2}) \]

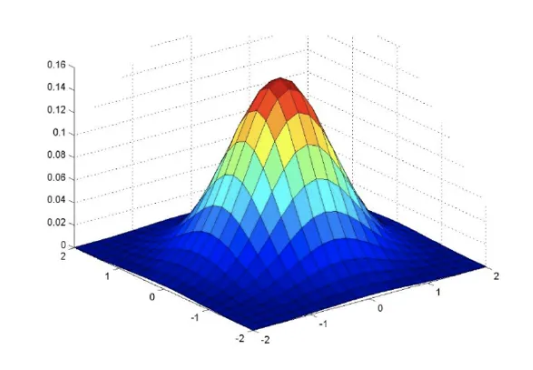
../../_images/gaussian.png — 图 7.7 高斯滤波器的形状#

其中 \(\sigma\) 是方差。在实际使用时，我们可以截取中心附近的一个 \((2k+1) \times (2k+1)\) 的区域计算每个点上的权重并归一化，然后按照均值滤波一样的方式进行卷积。高斯滤波器比均值滤波器的优势在于：我们可以数学上证明高斯核的傅里叶变换依然是一个高斯函数。因此，高斯卷积核能够更好地分离低频和高频分量，避免在模糊化时产生走样，效果如图 7.6 所示。

7.1.3. 边缘提取#

边缘滤波器（edge filter） 的作用是提取出图片中的边缘，输出图片只会保留输入图片中的边界部分。所谓“边界”，就是指图像中一个颜色块过渡到另一个颜色块的交界处，所以边界上的颜色变化比较大，换言之，梯度较大。利用这一点，我们可以借助一个估计梯度的算子来提取边界。我们可以构造两个滤波器分别计算图片在两个方向的梯度：

(7.7)#\[\begin{split} \mathbf G_x=\begin{bmatrix}-1&0&1\\-2&0&2\\-1&0&1\end{bmatrix},\ \mathbf G_y=\begin{bmatrix}1&2&1\\0&0&0\\-1&-2&-1\end{bmatrix} \end{split}\]

可以从公式中发现 \(\mathbf{G}_x\) 可以提取水平方向的梯度，而在竖直方向做了模糊；\(\mathbf{G}_y\) 则正好相反。应用这两个滤波器的结果如图 7.8 所示。

../../_images/edge_original.png — 图 7.8 从左到右：原图，使用水平滤波 \(\mathbf{G}_x\)，使用竖直滤波器 \(\mathbf{G}_y\)#

../../_images/edge_horizontal.png — 图 7.8 从左到右：原图，使用水平滤波 \(\mathbf{G}_x\)，使用竖直滤波器 \(\mathbf{G}_y\)#

如果想要检测到各个方向的边缘，我们需要同时考虑两个方向的梯度，比如考虑梯度的模长：

(7.8)#\[ \|\nabla a[x,y]\|=\sqrt{\left(\frac{\partial a[x,y]}{\partial x}\right)^2+\left(\frac{\partial a[x,y]}{\partial y}\right)^2}.\notag \]

我们可以在应用了公式 (7.7) 中的滤波器之后，再求公式 (7.8) 中的模长，得到最后的结果，如图 7.9 所示。

../../_images/edge_church.png — 图 7.9 使用 Sobel 滤波器提取边缘的结果#

../../_images/edge_sobel.png — 图 7.9 使用 Sobel 滤波器提取边缘的结果#

这样提取边缘的滤波器称为 Sobel-Feldman 滤波器，由 Irwin Sobel 和 Gary M. Feldman 合作提出。注意由于滤波器里包含了取模长的操作，Sobel-Feldman 滤波器就不再是线性滤波器了。

除了使用一阶导，我们还可以使用二阶导来提取边缘。在一维情况下，\(f[x]\) 的二阶导可以计算为：

(7.9)#\[ \frac{\partial^2}{\partial x^2} f[x] = (f[x+1] - f[x]) - (f[x] - f[x-1]) = f[x+1] - 2f[x] + f[x-1] \]

这可以对应到卷积核为 \([1, -2, 1]\) 的卷积过程。在二维中，我们可以使用连续情况下的拉普拉斯算子（Laplacian operator）：\(\nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}\)，类似一维情况，其对应的二维卷积核为：

(7.10)#\[\begin{split} \mathbf{L} = \begin{bmatrix} 0&1&0\\ 1&-4&1\\ 0&1&0 \end{bmatrix} \end{split}\]

这个卷积核称为 Laplacian 卷积核，其效果如图 7.10 所示。

../../_images/EdgeDetectors_Original.png — 图 7.10 使用 Laplacian 滤波器提取边缘的结果[2]#

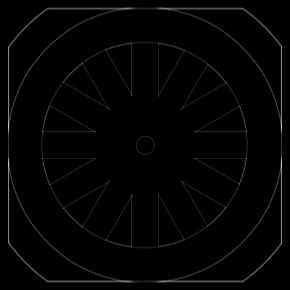
../../_images/EdgeDetectors_Laplacian.png — 图 7.10 使用 Laplacian 滤波器提取边缘的结果[2]#

除了上面介绍的边缘提取滤波器外，还有 Roberts 滤波器，Scharr 滤波器，Canny 滤波器等等，这里就不展开了。