12.1. 二维几何变换

本节介绍的基础二维几何变换包括平移、旋转、缩放和剪切变换。随后，将引入齐次坐标的概念，用基础变换的矩阵形式复合来表示任意仿射变换。

12.1.1. 平移

对一个点 \((x,y)\) 增加一个偏移量 \((d_x, d_y)\)， 将其移动到新的位置 \((x',y')\)，即实现了平移（translation）操作，

\[ x'=x+d_x,\,y'=y+d_y\,. \]

将平移变换表示成矩阵形式，设原始图形为 \(\mathbf{P}\)，偏移量表示为 \(\mathbf{D}\)，偏移后的图形为 \(\mathbf{P}'\)，有

(12.1)\[\begin{split} \mathbf{P}= \begin{bmatrix} x \\ y \end{bmatrix},\, \mathbf{P}'= \begin{bmatrix} x' \\ y' \end{bmatrix},\, \mathbf{D}= \begin{bmatrix} d_x \\ d_y \end{bmatrix}. \end{split}\]

从而平移可以抽象为 \(\mathbf{P}'=\mathbf{P}+\mathbf{D}\)。

平移是移动对象但不改变其形状的刚体变换。线段的平移可以通过移动端点，再重新绘制端点间的部分，多边形移动可以通过移动顶点，再重新进行连线，平移是最常见的改变物体位置的变换。

12.1.2. 缩放

缩放（scaling）可以用来改变物体的大小，缩放的比例称为缩放系数 \((s_x,s_y)\)，

(12.2)\[ x'=x \cdot s_x,\,y' = y \cdot s_y\,. \]

或表示成矩阵形式 \(\mathbf{P}'=\mathbf{S} \cdot \mathbf{P}\)，其中

(12.3)\[\begin{split} \begin{aligned} \mathbf{S} = \begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix}. \end{aligned} \end{split}\]

当 \(s_x=s_y\) 时，缩放后的对象与原对象比例不变，称为一致缩放，不等时则称为差值缩放，\(0<\) 缩放系数 \(<1\)，对象变小，缩放系数 \(>1\)，对象变大。当缩放系数为负数时，会将变换对象进行翻转，特别的，产生镜像的变换称为反射（reflection）变换，关于 \(x\) 轴反射，关于 \(y\) 轴反射，关于原点对称的反射矩阵分别为，

(12.4)\[\begin{split} \begin{aligned} \mathbf{S}_x = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix},\, \mathbf{S}_y = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix},\, \mathbf{S}_o = \begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix}. \end{aligned} \end{split}\]

12.1.3. 旋转

旋转（rotation）变换需要指定旋转轴和旋转角度，将对象的所有顶点绕旋转轴旋转指定角度后，对象完成旋转变换。

对二维图形来说，旋转轴通常垂直图形所在平面，投影到平面上成为旋转点。以旋转点为原点为例，点 \((x,y)\) 绕原点逆时针旋转角度 \(\theta\) 可以表示为,

(12.5)\[\begin{split} \begin{aligned} x' = x \cos \theta - y \sin \theta\,, \\ y' = x \sin \theta + y \cos \theta\,. \end{aligned} \end{split}\]

用矩阵形式表示 \(\mathbf{P}'=\mathbf{R} \cdot \mathbf{P}\)，其中

(12.6)\[\begin{split} \begin{aligned} \mathbf{R} = \begin{bmatrix} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{bmatrix}. \end{aligned} \end{split}\]

我们可以很容易地验证 \(\mathbf{R}\) 矩阵是一个正交矩阵，满足 \(\mathbf{R}\mathbf{R^T}=\mathbf{R}^T\mathbf{R}=\mathbf{I}\)。但并不是所有的正交矩阵都是旋转矩阵。举一个简单的例子，公式 (12.4) 中的反射矩阵 \(\mathbf{S}_x\) 和 \(\mathbf{S}_y\) 是正交矩阵，但表示的不是旋转；而关于原点的反射矩阵 \(\mathbf{S}_o\) 是一个旋转矩阵，对应着旋转180度。事实上，我们可以验证所有行列式为 \(1\) 的正交矩阵都是旋转矩阵，而所有行列式为 \(-1\) 的正交矩阵可以写为旋转矩阵乘以反射矩阵。形式化地，所有特征值为 \(1\) 的正交矩阵构成了一个群，称为特殊正交群（Special Orthogonal Group），在二维情况下记为 \(SO(2)\)。 抽象地来说，二维旋转变换与 \(SO(2)\) 群里的元素一一对应，旋转角 \(\theta\) 和旋转矩阵 \(\mathbf{R}\) 只是 \(SO(2)\) 群的两种表示方法。在三维情况中我们会进一步讨论这个关系。

12.1.4. 剪切

剪切（shear）是使对象形状发生变化的变换，经过剪切的对象看起来像滑动内部夹层进行的变换，常见的剪切是沿 \(x\) 轴和沿 \(y\) 轴方向进行剪切。

相对于 \(x\) 轴的 \(x\) 方向剪切变换可表示成下列矩阵：

(12.7)\[\begin{split} \begin{bmatrix} 1 & a\\ 0 & 1 \end{bmatrix} \end{split}\]

可以验证这个矩阵不会改变 \(y\) 坐标的值，变换的结果如 图 12.1 所示。

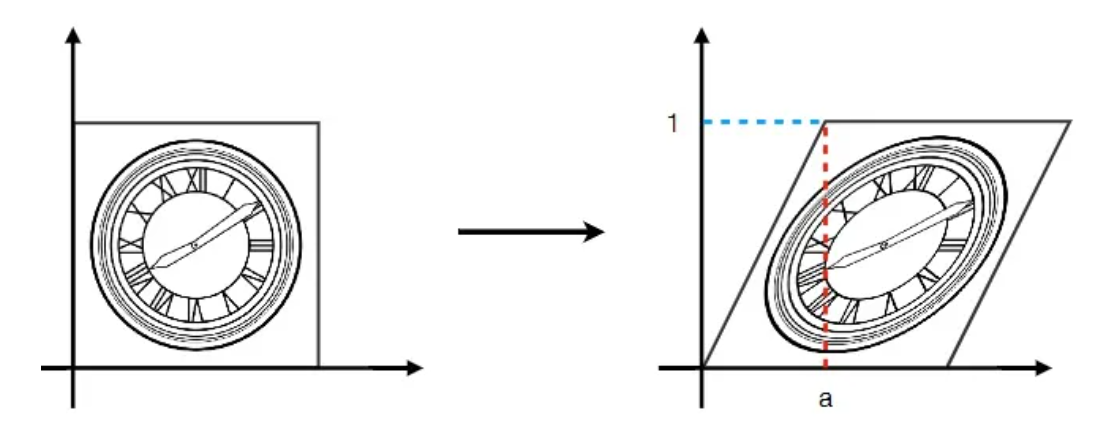
图 12.1 剪切变换。

一个有意思的结果是，二维的旋转可以分解为两个类似于剪切的变换的复合：

(12.8)\[\begin{split} \mathbf{R} = \begin{bmatrix} 1 & 0 \\ \tan \theta & \sec \theta \end{bmatrix} \begin{bmatrix} \cos \theta & -\sin \theta \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} \sec \theta & -\tan \theta \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ \sin \theta & \cos \theta \end{bmatrix}. \end{split}\]

分解中的每个变换可以看成缩放变换与剪切变换的复合。并且这些类似剪切变换都有一个特征，就是会固定一个维度不动，而对另外维度进行缩放与平移，比如最左边的矩阵对应的变换为

(12.9)\[ x' = x,\,y' = x\tan \theta + y\sec \theta \,. \]

这样分解的目的是什么？注意到分解得到的类似剪切变换是非常好实现的。如果我们想旋转一张图片，以公式 (12.9) 为例，我们可以逐行绘制像素，就像之前介绍的扫描线算法，并且各行之间是完全独立的，因此可以并行实现。因此这样的分解提供了图片旋转的快速实现方法 [CK01]，如 图 12.2 所示。

图 12.2 两次类似剪切变换等价于旋转变换。左：原图像，中：剪切一次，右：剪切两次。

12.1.5. 齐次坐标

二维空间下的齐次坐标（homogeneous coordinate），将二维坐标表示 \((x, y)\) 扩充为 \((x_w, y_w, w)\)，其中 \(w\) 被称为齐次参数，笛卡尔空间和齐次坐标的转换可以表示为，

\[ (\frac{x}{w},\frac{y}{w}) \Leftrightarrow (x, y, w)\,. \]

齐次坐标表示有很多好处：

齐次坐标的引入能够描述透视空间的特征。 在欧式空间中，同一平面的两条平行线不能相交。然而，在透视空间里面，两条平行线可以相交，例如：火车轨道随着我们的视线越来越窄，最后两条平行线在无穷远处交于一点。如果一个点在无穷远处，这个点的坐标将为 \((\infty,\infty)\)，在欧氏空间，这变得没有意义；而齐次坐标具有规模不变性，即对于所有的 \((wx,wy,w)\)，它们都对应欧氏空间中同一个点的 \((x,y)\)。从而求解欧氏空间中的平行线相交方程：

\[\begin{split} \left \{ \begin{aligned} Ax+By+C=0, \\ Ax+By+D=0. \end{aligned} \right. \end{split}\]

在笛卡尔坐标系中，\(C\neq D\) 意味着方程无解，但如果变换到齐次坐标系下，

\[\begin{split} \left \{ \begin{aligned} Ax+By+Cw=0, \\ Ax+By+Dw=0. \end{aligned} \right. \end{split}\]

则存在无穷远处的解 \((x_w, y_w, 0)\)。在后面的三维透视投影中我们能看到齐次坐标发挥更大的作用。

齐次坐标可以用来区分点和向量。 当 \(w \neq 0\) 时，\((x,y,w)\) 唯一对应笛卡尔坐标系下的点，而当 \(w=0\) 时，\((x,y,w)\) 则可以表示向量。

齐次坐标很适合表示线性变换。 注意到前面提到的平移操作，变换矩阵 \(\mathbf{D}\) 是 \(2\times 1\) 的矩阵，而旋转矩阵和缩放矩阵都是 \(2\times2\) 的矩阵，而在齐次坐标下，这些矩阵都能转变成 \(3 \times 3\) 的矩阵，且不再区分加法和乘法，所有的操作均变成了矩阵乘法。

\[\begin{split} \begin{aligned} \mathbf{D} = \begin{bmatrix} 1 & 0 & d_x \\ 0 & 1 & d_y \\ 0 & 0 & 1 \end{bmatrix}, \mathbf{R} = \begin{bmatrix} \cos \theta & - \sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix}, \mathbf{P} = \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix}. \end{aligned} \end{split}\]

12.1.6. 齐次坐标与仿射变换

如果坐标变换满足

\[\begin{split} \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} a_{xx} & a_{xy} & b_x \\ a_{yx} & a_{yy} & b_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}. \end{split}\]

则称该变换为仿射变换，变换后的坐标是原坐标的线性函数，且参数是常数。上述提及的平移、旋转、缩放和剪切变换都是仿射变换的一种特例。仿射变换由于同原坐标之间保持了线性关系，因此仿射变换的复合仍然是仿射变换。而且，我们可以将这些一个复杂的仿射变换拆分成简单的基础仿射变换。齐次坐标的引入使得这些仿射变换总是可以用矩阵来表示。举例来说，“绕特定点 \((a,b)\) 进行旋转 \(\theta\) 角”可以转变成“平移 \((-a,-b)\)” + “绕原点旋转 \(\theta\) 角” + “平移 \((a,b)\)”，对应的变换矩阵就是：

\[\begin{split} \begin{aligned} \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & a \\ 0 & 1 & b \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \cos \theta & - \sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & -a \\ 0 & 1 & -b \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}. \end{aligned} \end{split}\]

提示

由于矩阵乘法满足结合律，但不满足交换律，“先平移后旋转”和“先旋转后平移”对应着完全不同的几何变换。