9.1. 网格表示#
多边形网格模型是计算机图形学领域中最常用的几何表达方法,通过记录顶点和多边形来表示几何体的表面。 多边形网格模型是由一组顶点、边和面组成,这些定义了物体的形状。顶点是3D空间中的单一点,边是连接两个顶点的线,面是边的封闭环。面通常是三角形或四边形,并可用于表示曲面或其他复杂形状。这种表示方法有利于对几何体进行表面处理,但与点云相比需要更为复杂的数据结构。一个典型的多边形网络数据结构如 图 9.1 所示,由顶点列表、边列表和面列表构成。在某些应用中,人们还会设计一些额外的数据结构来方便邻居查找等常用操作,从而提高效率。值得一提的是,多面体的顶点数 \(v\)、边数 \(e\)、面数 \(f\) 满足 \(v-e+f=2\),这个规律被称为欧拉定理。
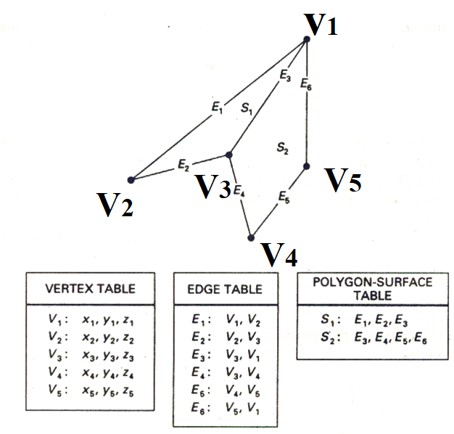
图 9.1 通过记录顶点表、边表和多边形表面表来表示一个多边形网格。#
多边形网格相较于其他几何表达有很多优点。它相对容易理解和使用,也能十分简便地进行渲染和几何形状处理。多边形网格也非常通用,它可以用来创建各种形状,从简单的立方体到复杂的角色。它还可以用于创建3D打印模型,以及逼真的动画和模拟。多边形网格具有很高的可扩展性。它可以用来创建任何大小的3D模型,从微小的物体到大型结构。图 9.2 展示了用网格模型表示各种形状的例子。

图 9.2 用网格模型表示几何体的例子。#
当然,如果要使用网格模型表达光滑的曲面,则需要大量的面片才能让模型变得精细,图 9.3 展示了面片数量较少时,网格模型表示曲面的能力有限。在几何处理章节(§11)中,我们将会专门介绍网格细分算法来增加网格模型的面片数量,从而使其趋近光滑曲面。
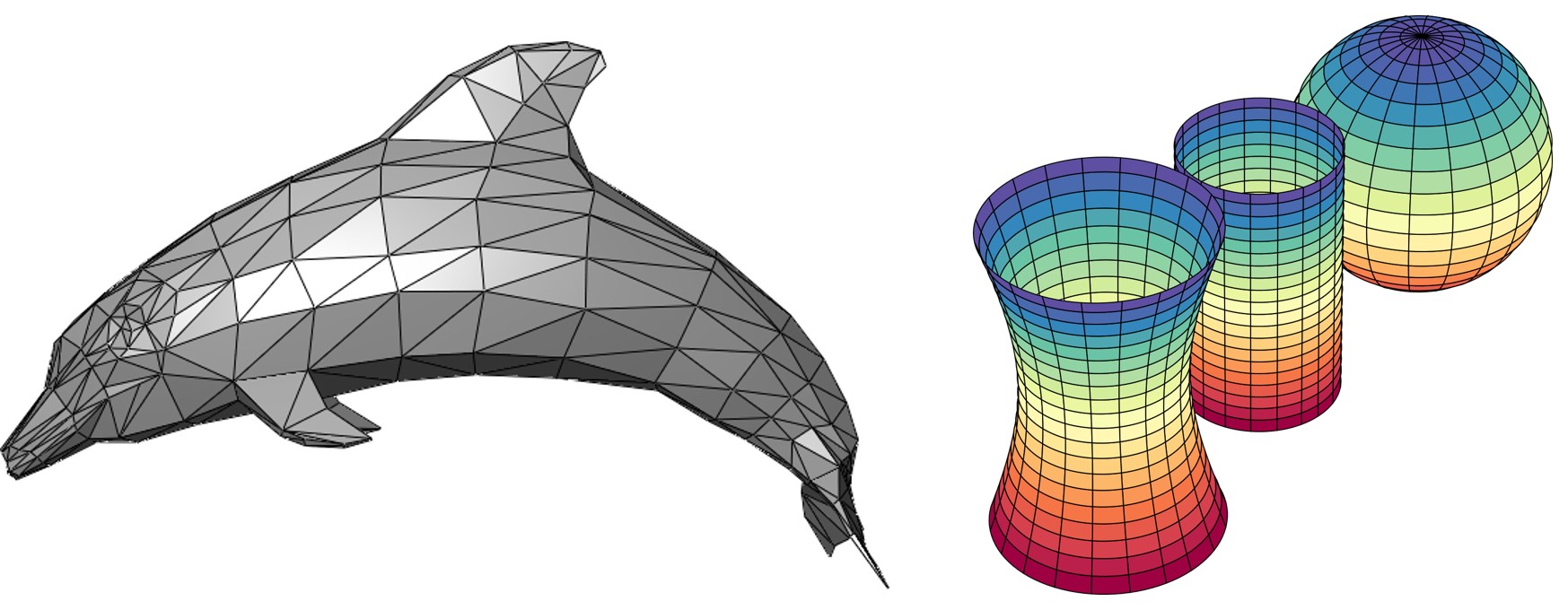
图 9.3 用网格模型表示曲面,从左到右使用的面片数量依次减少。可以看到当使用的面片数量较少时,得到的曲面就不够光滑。#
9.1.1. 三角网格#
三角网格是最常用的几何表示方式,可以地唯一表达一个几何体。常见的表示三角网格的数据结构是分别记录所有顶点(vertex)的三维坐标,以及每个三角面片(triangle facet)的三个顶点的索引(index),例如一个四面体就可以按照 图 9.4 的方式进行记录。这种数据结构通过共享顶点位置,减少了存储占用,同时保证了网格的整体性,即改变一个顶点在三维空间中的位置可以让与该顶点有关的所有三角面片发生移动。
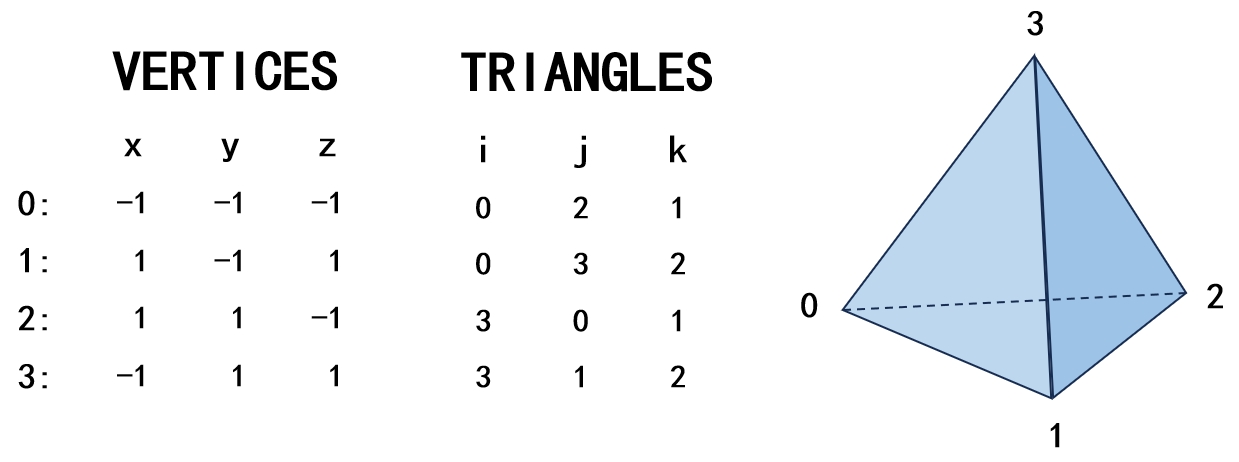
图 9.4 用三角网格表示一个四面体。#
9.1.2. 四边形网格#
四边形网格也是较为常用的一种网格表示,所有多边形面片全部是四边形构成,与三角网格一样,结构规整,易于存储。另外四边形网格的一大优点在于,其四边形特性在纹理映射贴图时的计算非常方便。
9.1.3. 网格参数化#
在计算机图形学中有一个非常独特的领域:网格参数化(mesh parameterization),它是将三维和二维联系起来的桥梁。 网格参数化是数字几何处理中非常重要的问题。其最早起源于纹理映射的需要。1974年,Catmull提出纹理映射技术,通过二维纹理空间和三维曲面之间的对应关系,计算三维曲面上每一点颜色值,如 图 9.5(a) 所示。这个过程需要建立三维曲面和二维纹理平面之间的一一映射,也就是参数化的过程,即计算三维空间曲面的每个网格顶点对应的两个纹理空间中坐标值 \((u,v)\)。
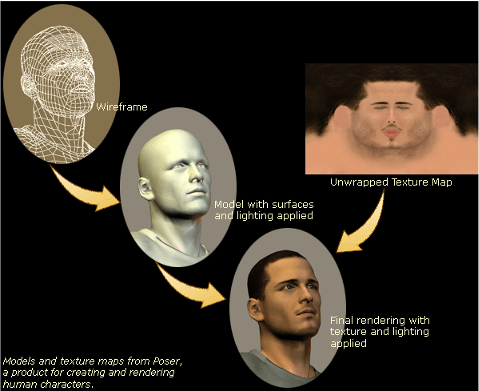 (a) 纹理映射。
(a) 纹理映射。
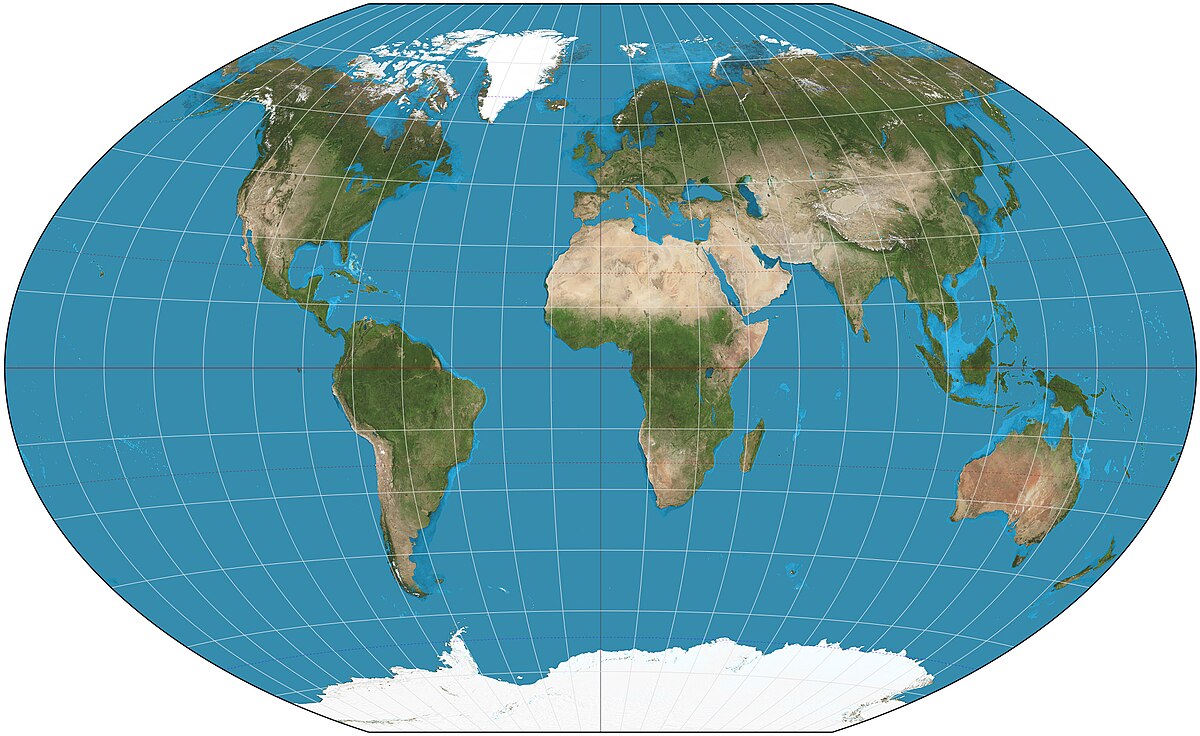 (b) 世界地图绘制。
(b) 世界地图绘制。
图 9.5 网格参数化的应用。#
参数化的另一个具体应用是世界地图的绘制 [1]。通常可以采用球面坐标系来表示地球表面的每一个点,给定半径后,每一个点对应着唯一一组方位角和仰角。但在实际应用中,是将世界地图画在平面上的,如 图 9.5(b) 所示。世界地图的绘制技术由来已久,出现了不同的技术,典型的有立体投影(或球极平面投影)、墨卡托投影等方法,如 图 9.6 所示。
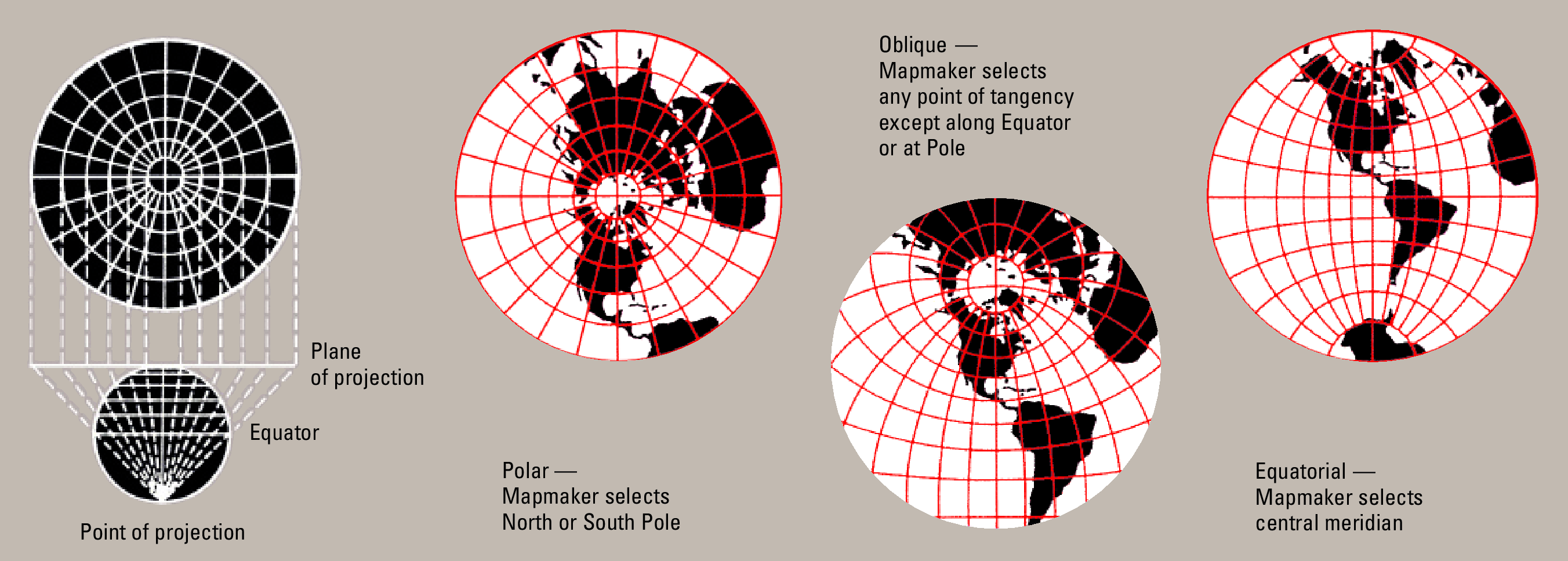 (a) 立体投影。
(a) 立体投影。
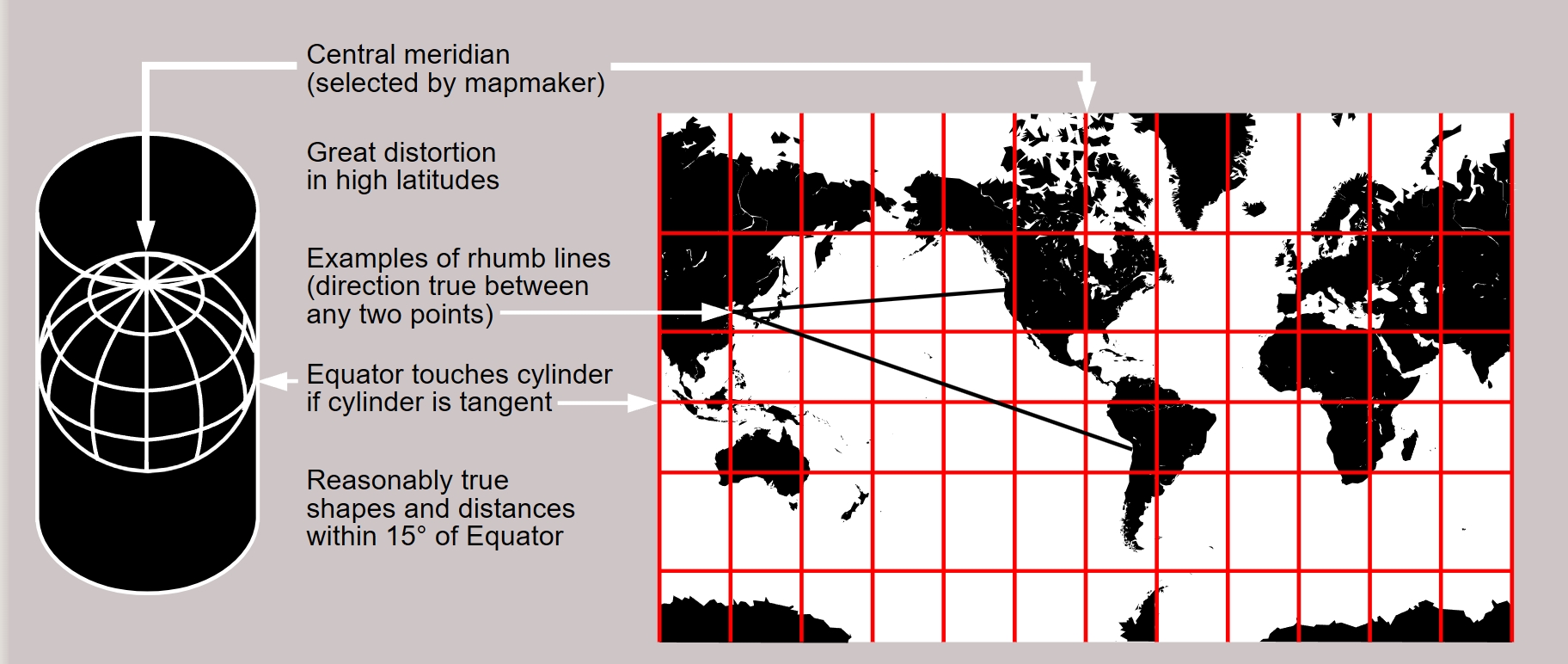 (b) 墨卡托投影。
(b) 墨卡托投影。
球极平面投影:将一个圆球面通过指定极点射影至一个平面的映射。能够保持角度不变,但是面积会发生改变,尤其在极点附近。
墨卡托投影:投影后经线是一组竖直的等距离平行直线,纬线是垂直于经线的一组平行直线。各相邻纬线间隔由赤道向两极增大。一点上任何方向的长度比均相等,即没有角度变形,而面积变形显著,随远离标准纬线而增大。该投影具有等角航线被表示成直线的特性,故广泛用于编制航海图和航空图等。
按照参数域的不同,网格参数化可以分为:
平面(planar)参数化,即将网格映射到平面;
球面(spherical)参数化,即将网格映射到规则的球面;
基域(simplicial)参数化,采用一个同构的简化模型作为参数域;
基于其它参数域的参数化。
按照参数化过程中保持哪种几何量,可以将参数化分为保长度(Isometric)的参数化、保角度(Conformal)的参数化、保面积(Equiareal)的参数化等等,即:将网格曲面映射到平面上时,分别保证长度、角度、面积不发生扭曲。事实上,保长度的映射等价于既保角度又保面积的映射。从三维网格表面映射到平面或其他参数域,理想的参数化是保形参数化,即保持局部形状不发生改变。这里的形状描述包括长度、角度、面积等几何度量。但理论上只有可展曲面(developable surface)存在保形参数化,如圆柱侧面,而一般的曲面在进行映射时都会发生不同程度的扭曲。
寻找网格表面顶点和平面上点之间的一一对应,又可以分为两种类型的平面参数化:
开网格参数化,这种情形下网格是具有边界的开网格,又分为固定边界映射和自由边界映射;
闭网格参数化,这种情形下网格构成一个封闭曲面,通常人为指定一条边界将封闭网格切开,然后转化为开网格进行参数化。
开网格的平面参数化中,最基础的模型是弹簧模型。如 图 9.7 所示,网格顶点作为图节点,网格边作为连接节点的边,形成多个弹簧连接的一个整体。建立从网格到纹理空间的参数化映射,也就是将每个网格顶点 \(\mathbf s_i=(x_i,y_i,z_i)\in\mathbb R^3\) 映射成二维参数空间中的点 \(\mathbf t_i=(u_i,v_i)\in \mathbb R^2\),我们可以采用弹簧系统的能量函数来描述参数化后的系统状态。弹簧的拉伸最后会达到平衡状态,使得整个系统能量最低,这个状态也就是参数化的最终结果。我们将总能量定义为加权的弹簧能量:
其中 \(n\) 是节点总数,\(D_{ij}\) 是连接第 \(i\) 和第 \(j\) 个顶点的弹簧的劲度系数,也是其所对应边在系统中的权重。
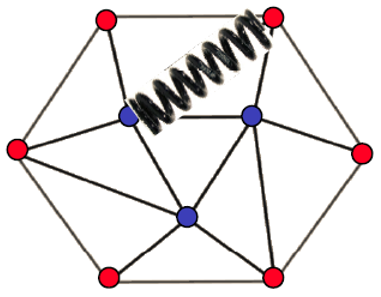
图 9.7 开网格平面参数化的弹簧模型。(a) 将网格建模成节点-弹簧模型。(b) 将三维空间中的网格点 \(\mathbf s=(x,y,z)\) 与二维参数空间中的点 \(\mathbf t=(u,v)\) 建立一一映射关系。#
这里的自变量即参数化后顶点 \(\mathbf t_i,\,i=1,\dots,n\) 对应的二维坐标。 那么平衡状态对应于关于变量的导数为零:
记系数 \(\lambda_{ij}=D_{ij}/\sum_{k\in\Omega(i)}D_{ik}\),可将上述式子整理为:
即,网格每个顶点在参数化后可以表示为相邻顶点的线性组合,组合系数 \(\lambda_{ij}\) 是连接该顶点的弹簧系数的加权平均,也被称为仿射组合系数。 在指定好组合系数之后,该方程变成关于顶点参数化坐标的线性方程组。对所有顶点的约束构成一个齐次方程组,包含 \(2n\) 个未知数和 \(2n\) 个线性方程。如果不增加约束条件,那么零解是其平凡解。可以通过对系统施加额外约束从而得到非平凡解。
一种约束条件采用固定边界映射,也称为重心坐标映射方法。将开网格边界上的顶点首先映射到指定的凸多边形边界上,例如正方形,那么这些顶点对应的参数化坐标在方程组中变为已知,从而可以求解内部顶点的参数化后的坐标。
另外,在弹簧系统中,可以通过设置合适的仿射组合系数来引导平面网格的参数化。特别的,这组仿射组合系数需要满足一些条件,例如凸组合,即保证凸多边形的加权平均仍然在凸多边形内部;线性重构,即如果网格本身是平面上的网格,组合后的点保持不变。常用的仿射组合系数有三种:
平均系数:\(\lambda_{ij}=\frac{1}{n_i}\),即设置为相邻顶点个数的倒数;
均值坐标系数:\(\lambda_{ij}=(\tan{\frac{\beta_{ji}}{2}}+\tan{\frac{\alpha_{ij}}{2}})/r_{ij}\),式中符号含义见 图 9.8;
调和坐标系数:\(\lambda_{ij}=(\cot{\gamma_{ij}}+\cot{\gamma_{ji}})/2\),只和角度有关,近似于保角映射。
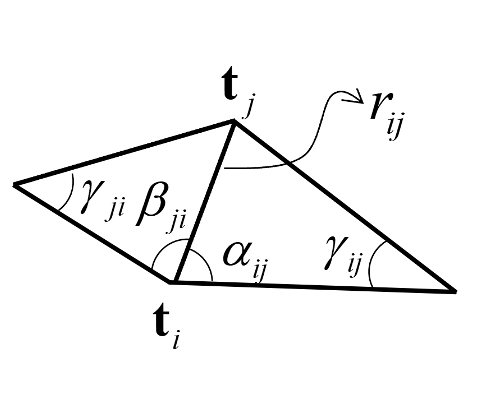
图 9.8 用边两侧的三角形中的量计算组合系数。#
9.1.4. 层次细节模型#
网格模型通过多边形表示几何形状的特点,决定了其所能表达的几何细节丰富程度与多边形的面数直接相关。实际应用场景中,我们往往既需要保证场景有着精细的建模,又要实时地对网格模型进行渲染和显示。由于计算开销,这两种需求之间往往存在矛盾:精细的模型有过多的多边形面数,会导致较慢的渲染速度;过于简单的模型又无法呈现足够的细节,造成渲染质量的下降。为了解决这一难题,层次细节模型(Level Of Detail,LOD)技术被提出。它基于一种简单的思想:当网格模型距离观察位置非常远时,即使用少量的多边形表示也不会导致渲染质量的显著下降,只有距离较近的网格模型才需要使用丰富的多边形面来保证细节的质量。因此,如果能够自适应地降低较远处物体的面数,提升近处物体的面数,让计算资源服务于更重要的部分,便能在渲染质量和渲染效率之间取得平衡。
层次细节模型就是这样一种技术,最简单的建立层次细节模型的方法就是预先对精细的模型进行不同程度的简化,然后缓存这些模型。随后,在渲染的过程中根据对象的距离确定所需要呈现的细节级别,从而选取对应的简化模型来加速渲染,如 图 9.9 所示。在 §11.3 中,我们会更详细地讨论网格模型的简化方法。
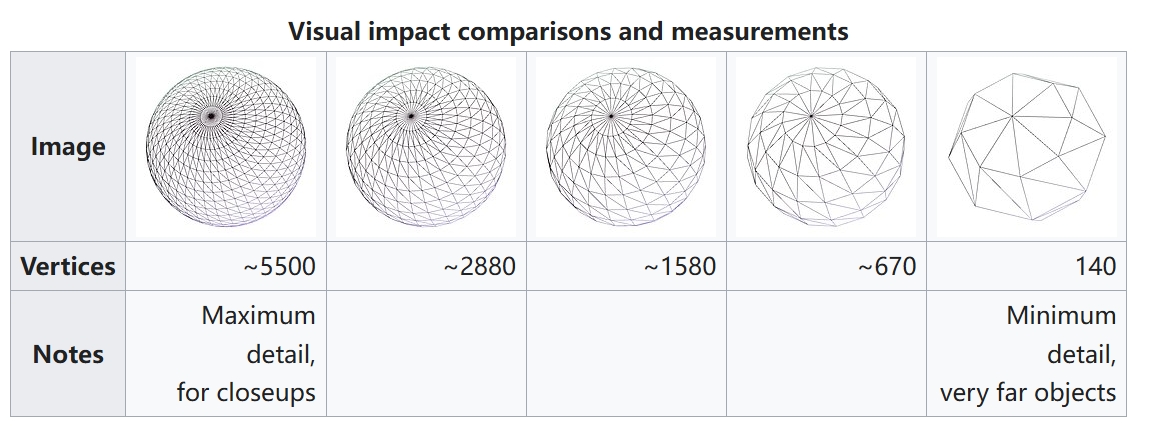
层次细节模型不仅可以应用于几何形状,还可以在纹理贴图中使用。Mipmap 贴图正是这样一种技术,通过预先计算一系列不同分辨率的纹理(典型的 Mipmap 贴图中,每一级的纹理宽度和高度都是上一级的一半),随后根据对象的距离确定所需要使用的贴图级别。这些方法往往都能够有效地提升实时渲染的性能。