曲线数学基础

6.1. 曲线数学基础#

6.1.1. 隐式表示与显式表示#

一般而言，我们可以把曲线或者曲面的表示方式可以分为显式表示（explicit representation） 和隐式表示（implicit representation） 两种。

显式表示通过给出曲线上的一系列点的坐标的值或函数表达式来表征曲线，较为直接和简单，比如大家熟悉的二次曲线：

(6.1)#\[ y = ax^2 + bx + c \]

然而 \(y=f(x)\) 不能表达像圆这样的不是函数的曲线。更一般地，我们通过参数化的方式来定义曲线，一条二维平面内的参数曲线（parametric curve） 可以表达为 \(f: t\in[a,\,b]\to\mathbb{R}^2\)，也即将一个自变量 \(t\) 映射到屏幕上的一个坐标 \((x, y)\)。例如，以原点为圆心、半径为 \(r\) 的圆的参数方程为：

(6.2)#\[\begin{split} \begin{align*} \begin{cases} x(t)=r\cos(t)\text{,}\\ y(t)=r\sin(t) \end{cases} \end{align*} \end{split}\]

其中 \(t\in[0,\,2\pi)\)，也被称为参数坐标。在这个例子中 \(t\) 对应圆周上点相对于圆心的角度，在更一般的例子中我们可以选择 \(t\) 为从初始点出发到当前点沿曲线的长度，这种参数的选择称为长度参数化。参数曲线的优点在于可以容易地得到曲线上点的坐标，应该也可以容易地可视化（只需要遍历参数坐标值就可以画出曲线的空间轨迹）。另外，将参数方程对参数坐标求导就可以得到曲线的梯度/切向方向。比如公式 (6.2) 梯度为：

(6.3)#\[ (x'(t), y'(t)) = (-r\sin (t), r\cos(t)) \]

正好对应圆的切线方向。

隐式表示与显示表示相对，不会直接给出参数到坐标的映射，而是通过隐式方程描述坐标应该满足的约束。比如在二维空间中，所有满足方程 \(x^2+y^2=1\) 的点 \((x,y)\) 构成的集合就对应二维平面上的单位圆。这种表达方式的一般形式可以写为 \(f(x,y)=0\)。我们在 §4.1 中构造的直线隐式方程也属于这一类。隐式表达的优点是容易对曲线的内部/外部或左侧/右侧进行区分。以单位圆方程 \(f(x,y)=x^2+y^2-1\) 为例，\(f(x_0,y_0)>0\) 表示 \((x_0, y_0)\) 在圆的外部，\(f(x_0,y_0)<0\) 表示 \((x_0, y_0)\) 在圆的内部。隐式表达的缺点在于难以采样，我们必须要通过得到隐式方程的解才知道哪些点在曲线上。因此如果我们想直观控制一条曲线的形状，显示表示是更好的方法。

6.1.2. 曲线的光滑性#

对于显示表示的曲线，理论上我们可以任意选择曲线方程 \((x(t),y(t))\)，然而为了曲线的可控性我们一般会选择多项式形式的曲线方程，也就是：

(6.4)#\[\begin{split} \begin{align*} \begin{cases} x(t)=a_nt^n+a_{n-1}t^{n-1}+\cdots+a_0\text{,}\\ y(t)=b_nt^n+b_{n-1}t^{n-1}+\cdots+b_0 \end{cases} \end{align*} \end{split}\]

更一般的，我们可以使用分段多项式来表达曲线。可以想象，如果不分段仅用一整个高阶曲线表达图 6.2 中的字母，我们可能需要非常高阶的多项式，并且精心计算每个参数，这无疑会带来设计和计算上的开销。因此，使用分段多项式是更为经济现实的做法。

但是分段会带来额外的问题，就是在连接处的光滑性。最简单的，我们可以在每一段都使用一阶多项式，也就是线段，然后首尾相接来表示曲线，如图 6.3 所示。我们观察相接点的情况，左右两侧的坐标是连续的，但是坐标的导数不连续，这种情况我们称为 \(C^0\) 光滑（\(C^0\) continuity）。

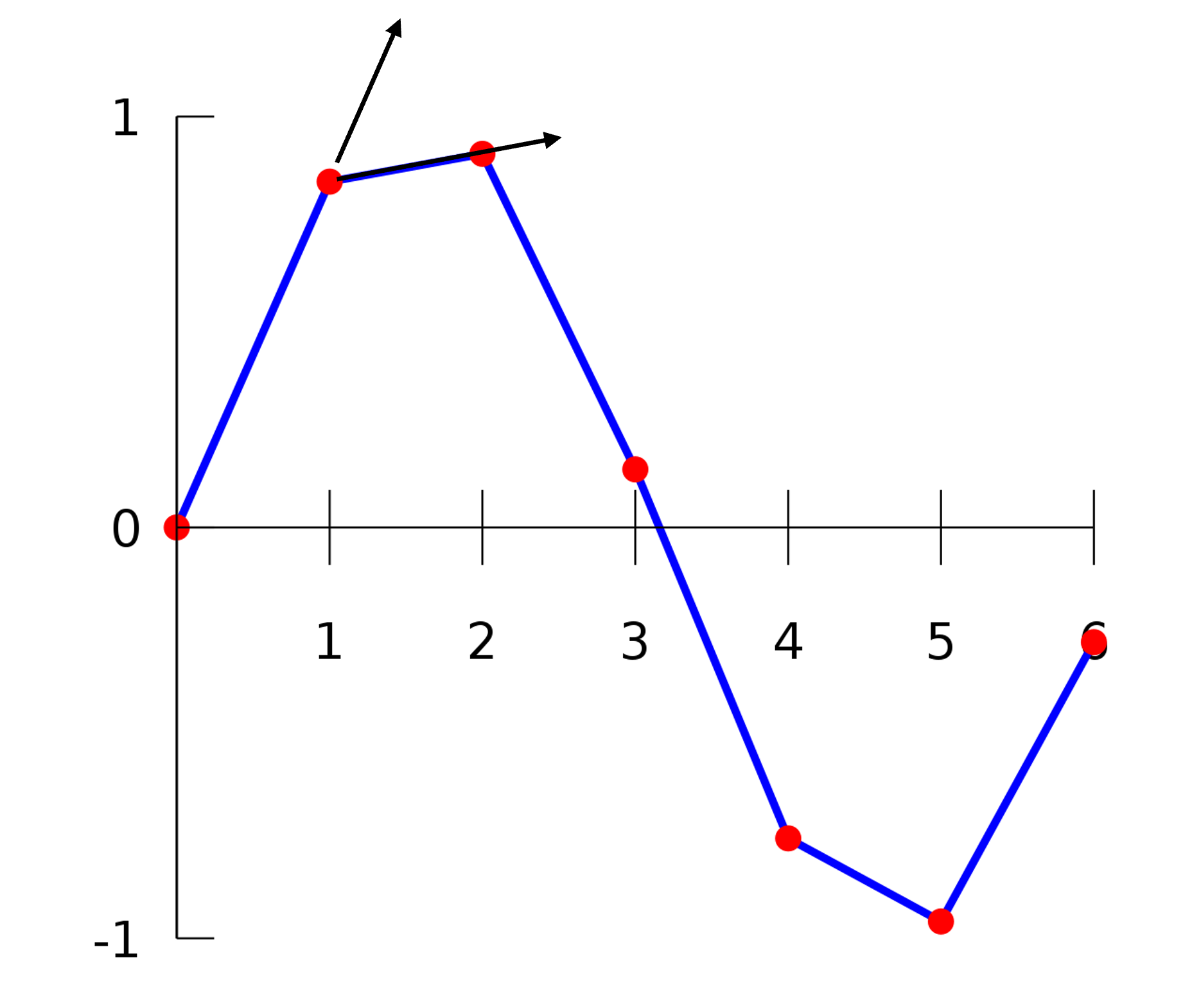
../../_images/c0.png

图 6.3 分段直线表示曲线#

如果我们使用更高阶的多项式表示每一段，并设法让连接处左右的导数也是连续的，也就是 \((x'(t), y'(t))\) 在左右两侧相等，那么此时我们就称曲线是 \(C^1\) 光滑（\(C^1\) continuity） 的。以此类推，我们可以定义 \(C^2\) 光滑是在 \(C^1\) 光滑的基础上要求二阶导数相等，\(C^3\) 光滑是在 \(C^3\) 光滑的基础上要求三阶导数相等，等等。更高的光滑性意味着我们能看到更连续的曲线，减少分段的影响。

但是注意，\(C^n\) 光滑性的定义是跟曲线的参数化相关的。对于同一条曲线，我们可以有不用的参数化方法。比如我们可以对参数坐标进行放缩：\((x,y)=(r\cos(at), r\sin(at))\) 和公式 (6.2) 表达的是同一个圆，相应的此时 \(t\in[0, 2\pi/a)\)。不同的参数化方法可以得出不同的梯度，但由于曲线的形状没有改变，我们其实只改变了梯度的大小，而没有改变梯度的方向。因此，我们可以得到另一套光滑性的定义 \(G^n\) 光滑（\(G^n\) continuity）：与 \(C^n\) 光滑相对，唯一的区别在于 \(G^n\) 光滑只强调曲线本身的几何属性，与参数化无关。比如 \(G^1\) 光滑要求曲线处处相切，\(G^2\) 光滑要求曲线的曲率处处连续等等。\(C^n\) 光滑的曲线一定 \(G^n\) 光滑，但是反之不一定。我们可以在工业设计中经常看到 \(G^n\) 光滑的描述，如图 6.4 所示。

../../_images/su7.png

图 6.4 小米汽车[1]设计生产的 Xiaomi SU7 汽车宣传使用了 G4 连续曲线设计顶面来降低风阻#

6.1.3. 插值与曲线#

在很多地方，我们可能看到插值（interpolation） 和曲线的概念一同出现，造成理解上的混乱。在数学上，插值指的是从一堆已有的数据点推测新的同类数据点的过程，因此插值的结果必须要包含已有数据点。对应到二维曲线中，如果我们有一堆散点，如果我们画出一条曲线经过了这些点，那么这个曲线就构成了原数据点插值，我们称这样的曲线为插值曲线（interpolation curve）。然而，图形学中的曲线有控制点（control point） 的概念，这些点可以控制曲线的形状，但是曲线不一定必须要经过这些点。所以曲线是不是插值曲线的关键，就在于曲线是否经过了所有控制点。插值性是非常好的性质，意味着我们可以直接控制曲线经过哪些地方，比如在画图中就很有用，但这不是构成曲线的必须要求。

6.1.4. 基函数#

我们使用最简单的线性插值的例子介绍基函数（basis function） 的概念。

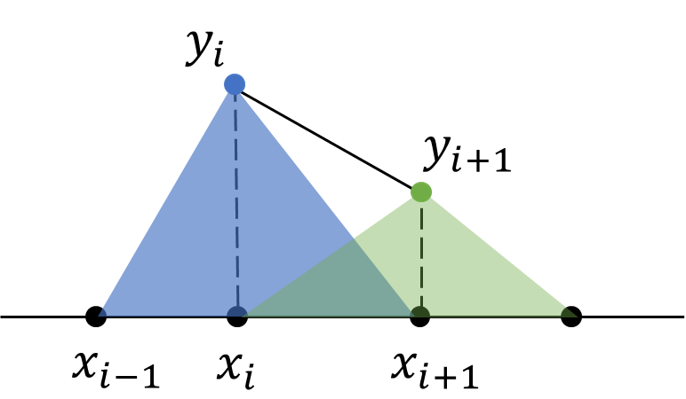
../../_images/basis.png

图 6.5 线性插值的基函数#

如图 6.5 所示，\([x_i, x_{i+1}]\) 之间的线性插值结果可以表示为：

(6.5)#\[ y = \frac{x_{i+1} - x}{x_{i+1} - x_i} y_i + \frac{x - x_i}{x_{i+1} - x_i} y_{i+1} \]

这是一条 \(y\) 关于 \(x\) 的直线并且经过两个端点。将所有分段的函数拼接起来就得到了最终插值结果 \(y(x)\)，这是一个分段线性函数。在这个例子中，我们可以定义每个基函数上的基函数 \(B_i(x)\) 为：

(6.6)#\[\begin{split} B_i(x) = \begin{cases} \frac{x - x_{i-1}}{x_i - x_{i-1}}, & x \in [x_{i-1}, x_i] \\ \frac{x_{i+1} - x}{x_{i+1} - x_i}, & x \in [x_i, x_{i+1}] \\ 0, & \text{else} \end{cases} \end{split}\]

\(B_i(x)\) 的形状就是图 6.5 中的蓝色三角形：在第 \(i\) 个节点处取 1，在其他节点取 0，中间线性变化。使用基函数我们可以将公式 (6.5) 重写为：

(6.7)#\[ y = B_i(x) y_i + B_{i+1} y_{i+1} \]

事实上，由于基函数在所有区间上都有定义，只不过大部分都是 0，我们可以将整个分段直线的插值结果写为：

(6.8)#\[ y = \sum_{i} B_i(x) y_i \]

从公式 (6.8) 可以发现，使用基函数可以将插值写为非常简洁的形式，并且我们也能使用这个形式理解插值的本质。不同的插值方法可以对应到不同的基函数的选择，但是为了使得插值的结果经过所有数据点，基函数需要满足

(6.9)#\[\begin{split} B_i(x_j) = \delta_{ij} = \begin{cases} 1, & i = j\\ 0, & i\neq j \end{cases} \end{split}\]

将公式 (6.9) 代入公式 (6.8) 中，我们就可以发现在 \(x_i\) 上 \(y\) 的值一定是 \(y_i\)。换句话说，只要能够写为公式 (6.8) 的形式，并且基函数满足公式 (6.9) ，我们就能得到一个合理的插值方法。并且插值的很多性质，比如光滑性、局部性都能对应到基函数的性质上来。