22.1. 刚体动力学

在力学中，刚体是一个理想化的物理模型，我们对这个模型的基本假设是它不会产生任何形变；用更严谨的说法讲，刚体是一种任意两个质点之间的距离在运动过程中保持不变的物体。生活中我们遇到的一些比较坚硬的物体都不是刚体，因为它们在受力时总会产生微小的形变，只不过肉眼看不到——严格来讲它们应该属于劲度（stiffness）很强的弹性体。事实上，物体只有发生形变才可能产生抵抗的作用力，在力学中刚体的受力情况其实是取物体形变程度趋于零的极限得到的。

22.1.1. 刚体的运动

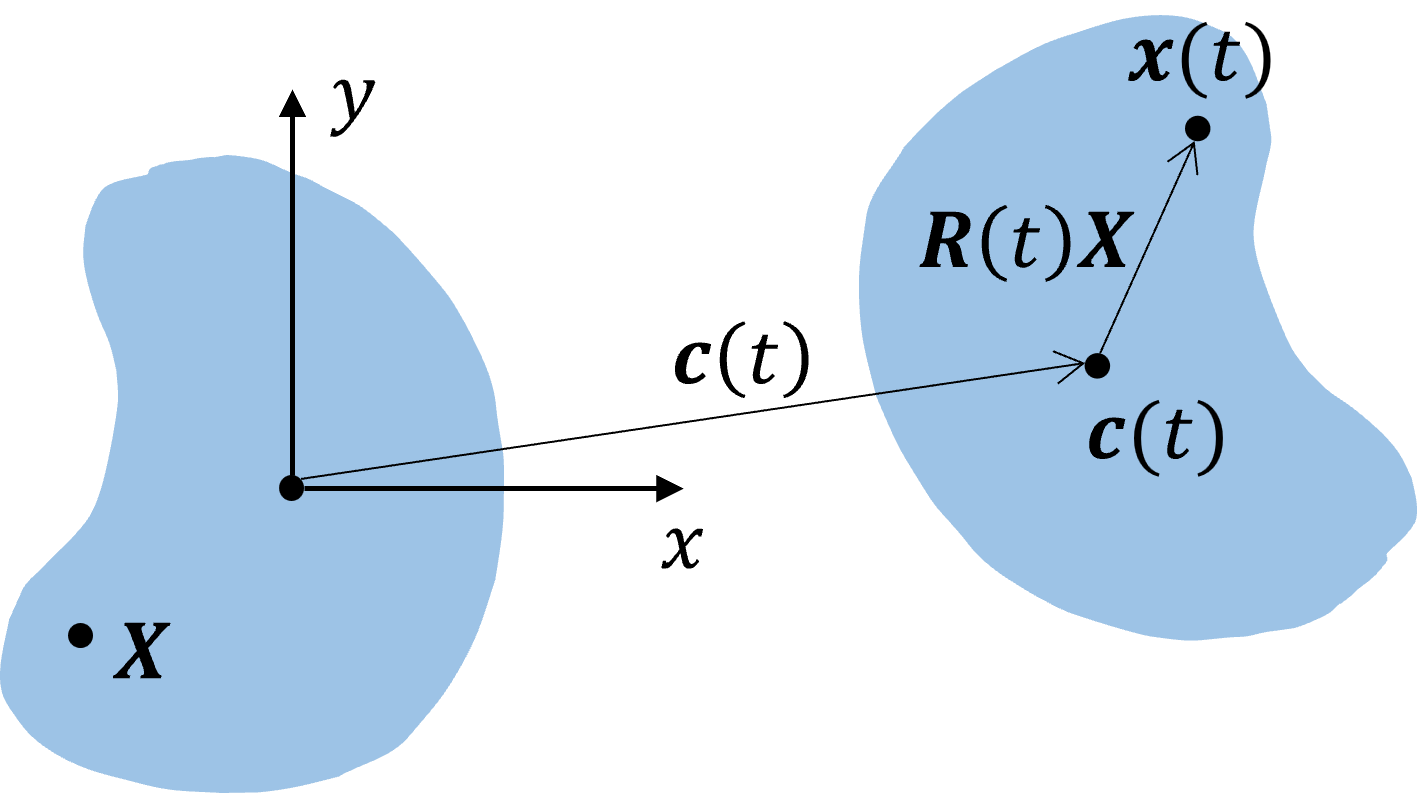
图 22.1 坐标系的选择以及刚性运动的描述

在 §21.2 中我们已经了解了什么是刚性运动（还记得超弹性体的能量要满足刚性运动下的不变性吗？），即只包含平移和旋转的运动。事实上，这个结论可以从刚体的定义推导出来。接下来，如图 22.1 所示，我们将参考构型下刚体的质心为原点构造直角坐标系，并且选取质心为参考点（即刚体在任一时刻的旋转都认为是关于质心的旋转），那么参考构型下的任意一点 \(\boldsymbol X\) 与刚体经过一系列运动后该点位置 \(\boldsymbol x\) 的关系可以表示为

(22.1)\[ \boldsymbol x(t)=\boldsymbol R(t)\boldsymbol X+\boldsymbol c(t)， \]

其中 \(\boldsymbol R\) 是旋转矩阵，\(\boldsymbol c\) 是运动后刚体的质心；这里我们将和运动时间 \(t\) 有关的量写成了函数的形式。通过式 (22.1) 我们自然可以想到，如果需要刻画刚体的运动，需要分别研究好 \(\boldsymbol c(t)\) 和 \(\boldsymbol R(t)\)，它们分别对应于刚体的平动和转动。

22.1.1.1. 刚体的平动

刚体的平动完全由质心的运动刻画，我们可以直接将整个刚体看成位置与质心重合的质点，因此刚体平动的速度 \(\boldsymbol v\) 与质心位置的关系是 \(\boldsymbol v=\dot{\boldsymbol c}\)。

22.1.1.2. 刚体的转动

由刚体的定义可以推出任意两点在任一时刻的相对速度与它们的相对位置正交，利用这个结论，我们可以证明绕定点转动的刚体一定存在唯一一个过该点的转动瞬轴（instantaneous axis），即在其上的任一质点速度为 \(\mathbf 0\) 的轴。证明方法可以参考 [00]，大体思路就是找到刚体上两个具有不平行速度的质点，过它们分别作两个垂直于速度方向的平面，交线就是转动瞬轴，如图 22.2 所示。

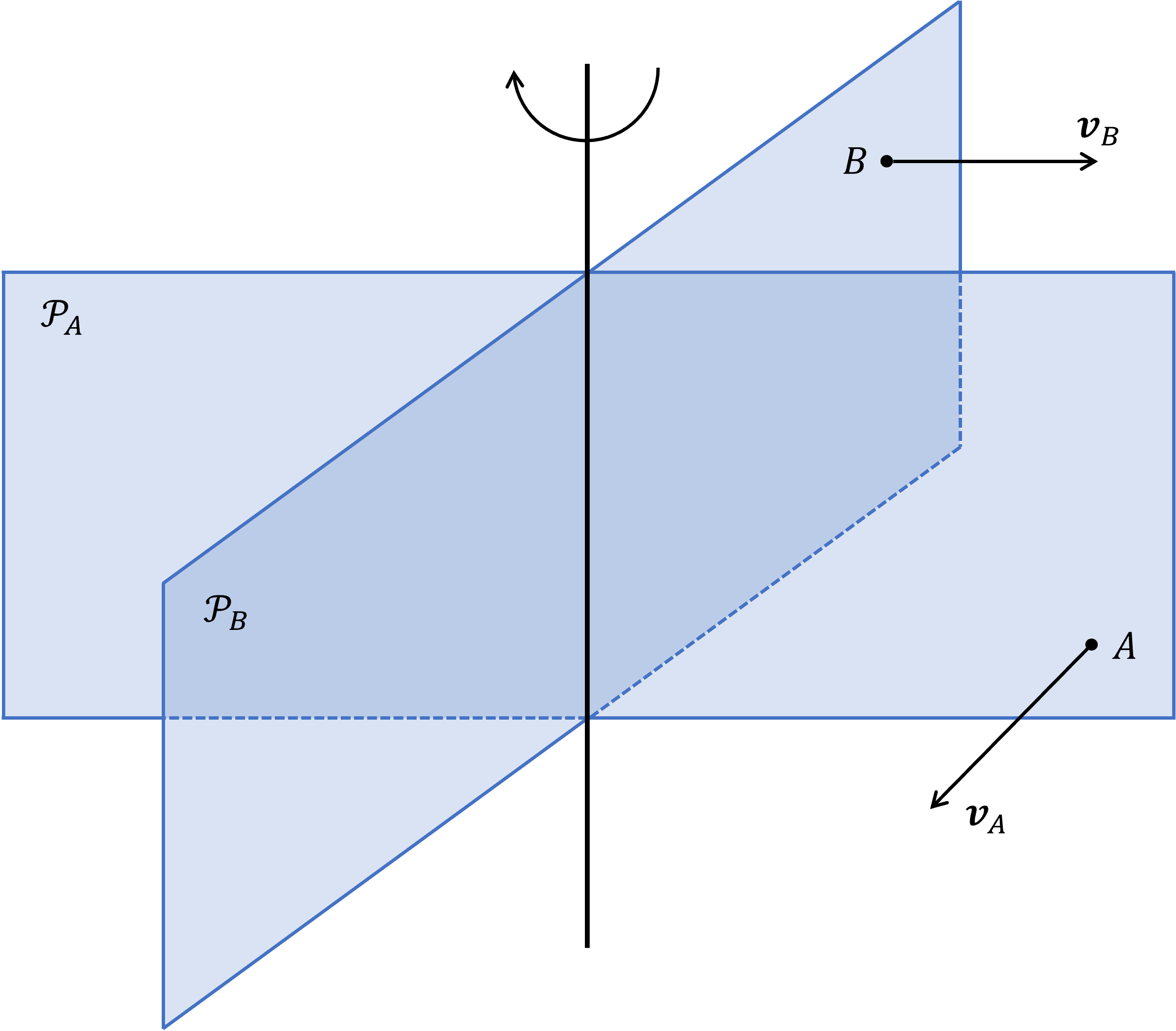
图 22.2 通过刚体质点的速度确定转动瞬轴：取两个速度方向不平行的质点 \(A\) 和 \(B\)，过 \(A\) 作垂直于 \(\boldsymbol v_A\) 的平面 \(\mathcal P_A\)，过 \(B\) 作垂直于 \(\boldsymbol v_B\) 的平面 \(\mathcal P_B\)，\(\mathcal P_A\) 与 \(\mathcal P_B\) 的交线即为转动瞬轴。

如果我们将刚体每一时刻的位置都统一减去质心的位置，那么剩下的部分就是刚体绕质心的转动，在每一时刻都存在一个转动瞬轴。借助“任意两点在任一时刻的相对速度与它们的相对位置正交”这个结论，读者不难推理出刚体每个质点上的速度构成的速度场就是围绕着转动瞬轴的涡，并且速度的大小与质点到转动瞬轴的位置成正比。

提示：证明刚体质点速度的性质

由于任意两点在任一时刻的相对速度与它们的相对位置正交，且转动瞬轴上所有质点的速度均为 \(\mathbf 0\)，读者可以尝试证明：任意一个不在转动瞬轴上质点的速度必然垂直于转动瞬轴与质点质心连线张成的平面，由此可以立即得到速度场是绕着转动瞬轴的旋转。

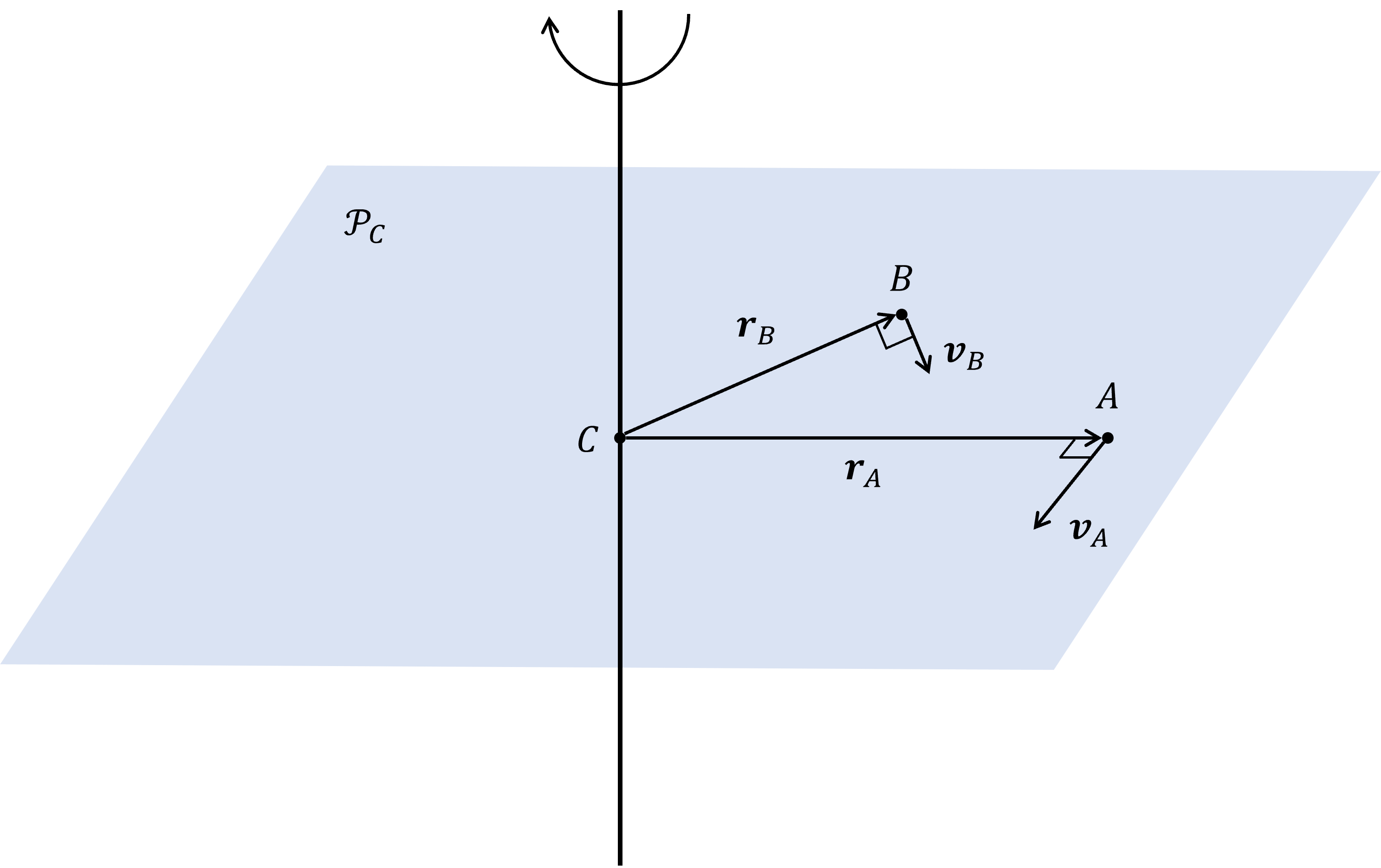
图 22.3 在垂直于转动瞬轴的平面 \(\mathcal P_C\) 上证明速度的大小与到轴的距离成正比

若希望证明速度的大小与质点到转动瞬轴的位置成正比，我们可以只在过质心与转动瞬轴垂直的平面 \(\mathcal P_C\) 上证明此结论，对于空间中的其他点，其速度等于该点在 \(\mathcal P_C\) 上投影点处的速度。如图 22.3，设质心为点 \(C\)，在 \(\mathcal P_C\) 上再取两点 \(A\)、\(B\) 使得 \(A\)、\(B\)、\(C\) 不共线，记向量 \(CA\) 和 \(CB\) 分别为 \(\boldsymbol r_A\) 和 \(\boldsymbol r_B\)，\(A\)、\(B\) 的速度分别为 \(\boldsymbol v_A\) 和 \(\boldsymbol v_B\)，那么我们有

\[\begin{split} \boldsymbol r_A\cdot\boldsymbol v_A=\boldsymbol r_B\cdot\boldsymbol v_B=0，\\ (\boldsymbol r_A-\boldsymbol r_B)\cdot(\boldsymbol v_A-\boldsymbol v_B)=0， \end{split}\]

其中 \(\cdot\) 表示向量的内积。通过这些等式可以立即得到

\[ \boldsymbol r_A\cdot\boldsymbol v_B=-\boldsymbol r_B\cdot\boldsymbol v_A， \]

这等价于

\[ \Vert\boldsymbol r_A\Vert\cdot\Vert\boldsymbol v_B\Vert\cos\langle\boldsymbol r_A,\boldsymbol v_B\rangle=-\Vert\boldsymbol r_B\Vert\cdot\Vert\boldsymbol v_A\Vert\cos\langle\boldsymbol r_B,\boldsymbol v_A\rangle。 \]

由于 \(\boldsymbol r_A\)、\(\boldsymbol r_B\) 不共线，所以等式两边的三角函数必不为零，再利用 \(\boldsymbol r_A\) 与 \(\boldsymbol v_A\) 垂直、\(\boldsymbol r_B\) 与 \(\boldsymbol v_B\) 垂直且等式两边三角函数必须反号，读者不难推出 \(\cos\langle\boldsymbol r_A,\boldsymbol v_B\rangle=-\cos\langle\boldsymbol r_B,\boldsymbol v_A\rangle\)，于是得出向量模长的关系 \(\frac{\Vert\boldsymbol r_A\Vert}{\Vert\boldsymbol r_B\Vert}=\frac{\Vert\boldsymbol v_A\Vert}{\Vert\boldsymbol v_B\Vert}\)，这也正是我们希望证明的速度大小的关系。

到这里读者不难发现，刚体上所有质点的速度的总自由度其实很少，我们只需要知道转动瞬轴的方向，以及一个能够表示速度大小的量，就能够还原出整个刚体的转动速度。角速度（angular velocity）便是这样一个描述刚体转动有多快的量，它是一个三维矢量，记为 \(\boldsymbol\omega\)；其方向与转动瞬轴平行，刚体的转动方向遵循右手定则，即当 \(\boldsymbol\omega\) 指向自身时看到的刚体是逆时针转动的；其大小又记为不加粗的 \(\omega\)，表示刚体每秒钟旋转的圈数，单位为秒的负一次方（\(\mathrm s^{-1}\)），因此角速度又称为角频率向量（angular frequency vector）。

通过上述对刚体质点上速度的研究，我们不难证明：若刚体质心固定，对于任一质点，设质心到该点的向量为 \(\boldsymbol r\)，则该点的速度为 \(\boldsymbol\omega\times\boldsymbol r\)。这也对应于式 (22.1) 中旋转部分的速度，即

(22.2)\[ \dot{\boldsymbol R}\boldsymbol X=\boldsymbol\omega\times(\boldsymbol x-\boldsymbol c)=\boldsymbol\omega\times(\boldsymbol R\boldsymbol X)。 \]

22.1.2. 刚体力学

我们已经建立的刚体的状态（位置和方向）与速度和角速度之间的关系，接下来将会继续了解速度与角速度如何受外力的影响。

22.1.2.1. 力影响速度

刚体平动的加速度（也即质心的加速度）乘以刚体的质量就等于其所受的合外力，即

(22.3)\[ m\dot{\boldsymbol v}=m\ddot{\boldsymbol c}=\boldsymbol F， \]

其中 \(m\) 表示刚体的质量，\(F\) 表示其受到的合外力。式 (22.3) 的形式非常像牛顿第二定律，但二者并不能混为一谈，感兴趣的读者可以阅读以下对该式的证明。

Proof. 为了方便推理，我们将刚体近似成由 \(N\) 个质点组成的质点系统，并且所有的外力只会作用在质点上。我们分别记质点 \(i\) 的质量、位移、受到的外力为 \(m_i\)、\(\boldsymbol x_i\)、\(\boldsymbol f_i\)。另外，为了保持任意两个质点间的距离不变，质点之间还会存在内力，记质点 \(i\) 受到质点 \(j\) 作用的力为 \(\boldsymbol f^\mathrm{inner}_{ij}\)，由牛顿第三定律可知 \(\boldsymbol f^\mathrm{inner}_{ij}+\boldsymbol f^\mathrm{inner}_{ji}=\mathbf 0\)。

首先，由质心的定义 \(\boldsymbol c=\frac 1m\sum_i^Nm_i\boldsymbol x_i\) 等式两边分别对时间求二阶导数可以得到

\[ m\ddot{\boldsymbol c}=\sum_i^Nm_i\ddot{\boldsymbol x}_i。 \]

对每个质点应用牛顿第二定律，并考虑到质点 \(i\) 所受的力为其所受的外力以及其余质点作用于它的内力，上式可继续变化：

\[\begin{split} m\ddot{\boldsymbol c}&=\sum_{i=1}^Nm_i\ddot{\boldsymbol x}_i\\ &=\sum_{i=1}^N\left(\boldsymbol f_i+\sum_{j\ne i}\boldsymbol f^\mathrm{inner}_{ij}\right)\\ &=\sum_{i=1}^N\boldsymbol f_i+\sum_{i=1}^N\sum_{j=i+1}^N(\boldsymbol f^\mathrm{inner}_{ij}+\boldsymbol f^\mathrm{inner}_{ji})\\ &=\boldsymbol F。 \end{split}\]

22.1.2.2. 力矩影响角速度

为了描述力如何影响角速度，我们需要先引入力矩（torque）的概念，因为只有力矩才能与角速度的变化率建立直接关系。

Definition 22.1 (力矩)

设力 \(\boldsymbol F\) 的作用点为 \(A\)，选取参考点 \(O\)，记向量 \(OA\) 为 \(\boldsymbol r\)，则 \(\boldsymbol F\) 的力矩为

\[ \boldsymbol\tau=\boldsymbol r\times\boldsymbol F。 \]

力矩与角速度变化率的关系也可以表示成类似式 (22.3) 的形式，但在此前我们还需要引入惯性张量（inertia）的概念。

Definition 22.2 (惯性张量)

选取参考点 \(O\)，其位置记为 \(\boldsymbol x_O\)。

对于一个连续介质刚体而言，设其占据的区域为 \(\Omega\)，则它的惯性张量为

\[ \boldsymbol I=\int_\Omega(\Vert\boldsymbol r\Vert^2\mathbf I-\boldsymbol r\boldsymbol r^\top)\rho\mathrm d\boldsymbol x， \]

其中 \(\boldsymbol r=\boldsymbol x-\boldsymbol x_O\) 表示 \(O\) 到位置 \(\boldsymbol x\) 的位移矢量，\(\rho\) 为定义在 \(\Omega\) 上的刚体的密度场。

对于 \(N\) 个点的质点系统而言，设质点 \(i\) 的质量为 \(m_i\)，\(O\) 到质点 \(i\) 的位移为 \(\boldsymbol r_i\)，则该质点系统的惯性张量为

\[ \boldsymbol I=\sum_{i=1}^Nm_i(\Vert\boldsymbol r_i\Vert^2\mathbf I-\boldsymbol r_i\boldsymbol r_i^\top)。 \]

现在我们选取参考点为刚体的质心，那么对于刚体中的任一位置 \(\boldsymbol x\)，其关于参考点的相对位移 \(\boldsymbol r=\boldsymbol x-\boldsymbol c=\boldsymbol R\boldsymbol X\)（见式 (22.1)），所以只要我们知道参考构型下刚体的惯性张量 \(\boldsymbol I_\mathrm{ref}\)，就可以求得 \(t\) 时刻下刚体的惯性张量：

\[\begin{split} \boldsymbol I(t)&=\int_{\Omega(t)}(\Vert\boldsymbol r(t)\Vert^2\mathbf I-\boldsymbol r(t)[\boldsymbol r(t)]^\top)\rho(\boldsymbol x,t)\mathrm d\boldsymbol x\\ &=\int_{\Omega_\mathrm{ref}}(\Vert\boldsymbol R(t)\boldsymbol X\Vert^2\mathbf I-\boldsymbol R(t)\boldsymbol X\boldsymbol X^\top[\boldsymbol R(t)]^\top)\rho_\mathrm{ref}(\boldsymbol X)\mathrm d\boldsymbol X\\ &=\boldsymbol R(t)\left(\int_{\Omega_\mathrm{ref}}(\Vert\boldsymbol X\Vert^2\mathbf I-\boldsymbol X\boldsymbol X^\top)\rho_\mathrm{ref}(\boldsymbol X)\mathrm d\boldsymbol X\right)[\boldsymbol R(t)]^\top\\ &=\boldsymbol R(t)\boldsymbol I_\mathrm{ref}[\boldsymbol R(t)]^\top， \end{split}\]

这里我们使用了 \(\mathrm{ref}\) 下标表示参考构型下的量，并且也将和时间有关的量显式地表示成了关于 \(t\) 的函数，第二个等号用到了换元法以及 \(\mathrm d\boldsymbol x=\mathrm d(\boldsymbol{RX}+\boldsymbol c)=\mathrm d\boldsymbol X\) 这个体积微元的旋转和平移不变性的关系。这个结论对于质点系统同样有效，读者不妨自行证明。

在力矩与角速度变化率的关系可以表示为

(22.4)\[ \boldsymbol I\dot{\boldsymbol\omega}=\boldsymbol\tau-\boldsymbol\omega\times\boldsymbol{I\omega}， \]

其中 \(\boldsymbol\tau=\sum_i\boldsymbol\tau_i\) 为总力矩。我们同样可以借助质点系统对式 (22.4) 进行证明，感兴趣的读者可以阅读。

Proof. 我们继续使用上一个证明中的记号，另外记 \(\boldsymbol v_i=\dot{\boldsymbol x}_i\)，\(\boldsymbol a_i=\ddot{\boldsymbol x}_i\)。选取质心为参考点，并记 \(\boldsymbol r_i=\boldsymbol x_i-\boldsymbol c\) 为质点 \(i\) 相对质心的位移。那么质点 \(i\) 所受外力力矩为 \(\boldsymbol\tau_i=\boldsymbol r_i\times\boldsymbol f_i\)，质点系统的角动量（angular momentum）为

(22.5)\[ \boldsymbol J=\sum_{i=1}^N\boldsymbol r_i\times m_i\boldsymbol v_i。 \]

将式 (22.5) 两边对时间求导可得

\[\begin{split} \dot{\boldsymbol J}&=\frac{\mathrm d}{\mathrm dt}\sum_{i=1}^N(\boldsymbol x_i-\boldsymbol c)\times m_i\boldsymbol v_i\\ &=\sum_{i=1}^N(\boldsymbol v_i-\boldsymbol v)\times m_i\boldsymbol v_i+\boldsymbol r_i\times m_i\boldsymbol a_i\\ &=\sum_{i=1}^N\boldsymbol v_i\times m_i\boldsymbol v_i+\boldsymbol v\times\sum_{i=1}^Nm_i\boldsymbol v_i+\sum_{i=1}^N\boldsymbol r_i\times m_i\boldsymbol a_i\\ &=\sum_{i=1}^N\boldsymbol r_i\times\left(\boldsymbol f_i+\sum_{j\ne i}\boldsymbol f^\mathrm{inner}_{ij}\right)\\ &=\sum_{i=1}^N\boldsymbol\tau_i+\sum_{i=1}^N\sum_{j=i+1}^N(\boldsymbol r_i\times\boldsymbol f^\mathrm{inner}_{ij}+\boldsymbol r_j\times\boldsymbol f^\mathrm{inner}_{ji})\\ &=\sum_{i=1}^N\boldsymbol\tau_i+\sum_{i=1}^N\sum_{j=i+1}^N(\boldsymbol r_i-\boldsymbol r_j)\times\boldsymbol f^\mathrm{inner}_{ij}\\ &=\boldsymbol\tau， \end{split}\]

其中最后一步是因为两个质点之间的内力必然沿两点连线的方向。

将式 (22.1) 两边对时间求导，再利用式 (22.2) 可得 \(\boldsymbol v_i=\boldsymbol v+\boldsymbol\omega\times\boldsymbol r_i\)，将此代入式 (22.5) 可得

\[\begin{split} \boldsymbol J&=\sum_{i=1}^N\boldsymbol r_i\times m_i(\boldsymbol v+\boldsymbol\omega\times\boldsymbol r_i)\\ &=\left(\sum_{i=1}^Nm_i\boldsymbol r_i\right)\times\boldsymbol v+\sum_{i=1}^Nm_i\boldsymbol r_i\times(\boldsymbol\omega\times\boldsymbol r_i)\\ &=\sum_{i=1}^Nm_i[(\boldsymbol r_i\cdot\boldsymbol r_i)\boldsymbol\omega-(\boldsymbol r_i\cdot\boldsymbol\omega)\boldsymbol r_i]\\ &=\left(\sum_{i=1}^Nm_i(\Vert\boldsymbol r_i\Vert^2\mathbf I-\boldsymbol r_i\boldsymbol r_i^\top)\right)\boldsymbol\omega\\ &=\boldsymbol{I\omega}， \end{split}\]

其中第二行等号后的 \(\sum_{i=1}^Nm_i\boldsymbol r_i=\mathbf 0\)，\(\boldsymbol r_i\times(\boldsymbol\omega\times\boldsymbol r_i)=(\boldsymbol r_i\cdot\boldsymbol r_i)\boldsymbol\omega-(\boldsymbol r_i\cdot\boldsymbol\omega)\boldsymbol r_i\) 这个等式关系读者可以自行验证。上式的形式与动量与速度的关系 \(\boldsymbol p=m\boldsymbol v\) 在形式上十分相似，角动量 \(\boldsymbol J\) 与动量 \(\boldsymbol p\) 相对应，角速度 \(\boldsymbol\omega\) 与线速度 \(\boldsymbol v\) 相对应，惯性张量 \(\boldsymbol I\) 充当的就是质量 \(m\) 的角色。将上式的两边对时间求导可得

\[\begin{split} \boldsymbol\tau=\dot{\boldsymbol J}&=\dot{\boldsymbol I}\boldsymbol\omega+\boldsymbol I\dot{\boldsymbol\omega}\\ &=\boldsymbol I\dot{\boldsymbol\omega}+(\dot{\boldsymbol R}\boldsymbol I_\mathrm{ref}\boldsymbol R^\top+\boldsymbol R\boldsymbol I_\mathrm{ref}\dot{\boldsymbol R}^\top)\boldsymbol\omega\\ &=\boldsymbol I\dot{\boldsymbol\omega}+([\boldsymbol\omega]\boldsymbol I-\boldsymbol I[\boldsymbol\omega])\boldsymbol\omega\\ &=\boldsymbol I\dot{\boldsymbol\omega}+\boldsymbol\omega\times\boldsymbol{I\omega}， \end{split}\]

其中 \([\boldsymbol\omega]=\begin{bmatrix}0&-\omega_z&\omega_y\\\omega_z&0&-\omega_x\\-\omega_y&\omega_x&0\end{bmatrix}\) 为 \(\boldsymbol\omega\) 的叉乘矩阵，对于任一三维向量 \(\boldsymbol y\) 有 \([\boldsymbol\omega]\boldsymbol y=\boldsymbol\omega\times\boldsymbol y\)；第三个等号我们用了旋转矩阵的导数 \(\dot{\boldsymbol R}=[\boldsymbol\omega]\boldsymbol R\)，这可以借助式 (22.2) 通过 \(\boldsymbol X\) 的任意性推导出来。由此可立即得出式 (22.4)。

22.1.3. 刚体模拟的时间积分算法

我们在本节中通过列出刚体模拟的时间积分算法对上述介绍的结论进行总结。在模拟过程中需要维护的量包括刚体质心的位置 \(\boldsymbol c\)、平动速度 \(\boldsymbol v\)、旋转矩阵 \(\boldsymbol R\) 以及角速度 \(\boldsymbol\omega\)，此外我们需要知道或者与计算得到的量包括时间步长 \(h\)、刚体的质量 \(m\) 以及参考构型下的惯性张量 \(\boldsymbol I_\mathrm{ref}\)。那么在每个时间步需要依次执行以下步骤：

1. 计算外力 \(\boldsymbol F=\sum_i\boldsymbol f_i\) 和外力矩 \(\boldsymbol\tau=\sum_i(\boldsymbol R\boldsymbol X_i)\times\boldsymbol f_i\)。

2. 更新速度：\(\boldsymbol v\gets\boldsymbol v+\frac hm\boldsymbol F\)。

3. 更新质心位置：\(\boldsymbol c\gets\boldsymbol c+h\boldsymbol v\)。

4. 计算的当前惯性张量 \(\boldsymbol I=\boldsymbol R\boldsymbol I_\mathrm{ref}\boldsymbol R^\top\)。

5. 更新角速度：\(\boldsymbol\omega\gets\boldsymbol\omega+h\boldsymbol I^{-1}(\boldsymbol\tau-\boldsymbol\omega\times\boldsymbol{I\omega})\)。

6. 更新旋转矩阵：\(\boldsymbol R\gets\mathrm{rotvec\_to\_matrix}(h\boldsymbol\omega)\boldsymbol R\)。

在第 5 步我们需要求惯性张量的逆，首先对于体积非零的刚体而言 \(\boldsymbol I\) 一定可逆，其次 \(\boldsymbol I\) 是一个 \(3\times 3\) 的矩阵，求逆运算的开销不会很大，并且可以预计算出 \(\boldsymbol I_\mathrm{ref}^{-1}\)，并利用 \(\boldsymbol I^{-1}=\boldsymbol R\boldsymbol I_\mathrm{ref}^{-1}\boldsymbol R^\top\) 避免每个时间步都求一次逆。在第 6 步中的 \(\mathrm{rotvec\_to\_matrix}(\cdot)\) 运算可以参考 §19.1 中各种旋转表示之间的转换，注意这里不用 \(\dot{\boldsymbol R}=[\boldsymbol\omega]\boldsymbol R\) 的离散化形式是为了避免修改 \(\boldsymbol R\) 后不再是旋转矩阵。